Right Triangle
A right triangle is a triangle with one right angle (90°).
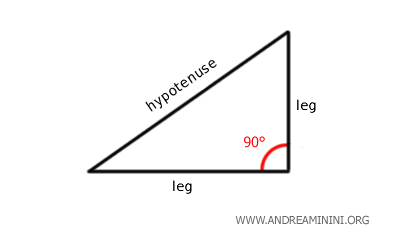
In a right triangle, the sides that form the right angle are called legs.
The side opposite the right angle is called the hypotenuse.
The right triangle is one of the simplest geometric shapes, yet it forms the foundation for many theorems, trigonometry, and numerous practical applications.
Interest in the right triangle dates back to ancient civilizations. The ancient Egyptians used it in the construction of the pyramids. Babylonian astronomers utilized trigonometric tables for their celestial calculations. The ancient Greeks, like Hipparchus, further developed trigonometry. The Greek mathematician Pythagoras gave his name to one of the most famous theorems: the Pythagorean theorem.
Pythagorean Theorem
In a right triangle, the sum of the areas of the squares built on the legs is equal to the area of the square built on the hypotenuse.
$$ a^2 + b^2 = c^2 $$
Where "a" and "b" are the lengths of the legs, and "c" is the length of the hypotenuse.
In other words, the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the legs.
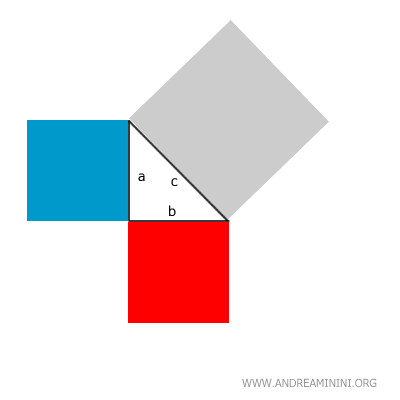
This implies that the hypotenuse is always the longest side in a right triangle.
By taking the square root of both sides
$$ \sqrt{c^2} = \sqrt{a^2 + b^2} $$
And simplifying, we get the most well-known form of the theorem:
$$ c = \sqrt{a^2 + b^2} $$
This formula revolutionized geometry and still has applications in various fields today, from physics to navigation. For instance, it is used to calculate the distance between two points.
Height of a Right Triangle Relative to the Hypotenuse
The height of a right triangle relative to the hypotenuse is equal to the product of the legs (a×b) divided by the hypotenuse (c): $$ h = \frac{a \times b}{c} $$ where \( a \) and \( b \) are the lengths of the legs, and \( c \) is the length of the hypotenuse.

This result comes from the fact that the area of the triangle can be expressed in different ways.
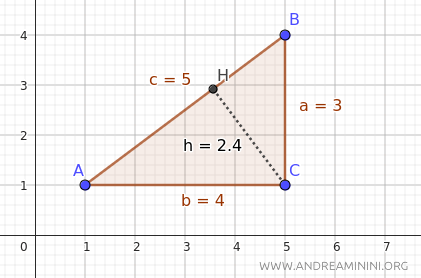
Example
Let's take this right triangle as an example, where we know all the side lengths.
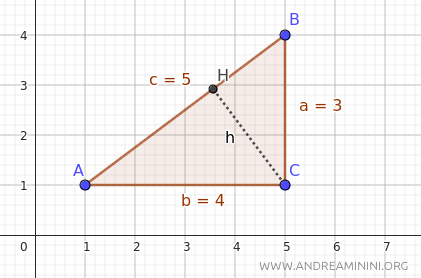
We want to calculate the height (h) relative to the hypotenuse (c).
To do this, we apply the following formula:
$$ h = \frac{a \times b}{c} $$
In this case, the legs are a=3, b=4, and the hypotenuse c=5.
$$ h = \frac{3 \times 4}{5} $$
$$ h = \frac{12}{5} $$
$$ h = 2.4 $$
The height relative to the hypotenuse is approximately h=2.4.
This result is correct as verified using GeoGebra.
Proof
Let's prove the formula for the height relative to the hypotenuse:
$$ h = \frac{a \times b}{c} $$
In general, the height (h) of a triangle (not just right triangles) relative to any side taken as the base is found using this formula:
$$ h = \frac{2 \cdot A}{\text{base}} $$
Where A is the area of the triangle, and "base" is the length of a side taken as the base.
The area of a right triangle is equal to half the product of the base and height.
$$ A = \frac{\text{base} \times \text{height}}{2} $$
In a right triangle, we can take one leg as the "base" and the other leg as the "height."

So, the area of the triangle becomes: $$ A = \frac{a \cdot b}{2} $$
Substituting the area A into the initial formula and simplifying:
$$ h = \frac{2 \cdot A}{\text{base}} $$
$$ h = \frac{2 \cdot ( \frac{a \cdot b}{2} )}{\text{base}} $$
$$ h = \frac{a \cdot b}{\text{base}} $$
Now consider the hypotenuse (c) as the base.
$$ h = \frac{a \cdot b}{c} $$
And this gives us the formula we wanted to prove.
The height (h) of a right triangle relative to the hypotenuse is equal to the product of the legs divided by the hypotenuse.
This result is particularly useful in more advanced geometric contexts. For example, in analytic geometry, I've used it to demonstrate the distance from a point to a line in the Cartesian plane.
Alternative Proof. To show that the height \( h \) of a right triangle relative to the hypotenuse is equal to the product of the legs divided by the hypotenuse, we can also use the relationship between the area of the triangle expressed in two different ways. Consider a right triangle with legs of lengths \( a \) and \( b \), and hypotenuse \( c \). The area \( A \) of the triangle can be expressed as half the product of the legs: $$ A = \frac{1}{2}ab $$ The area \( A \) of the triangle can also be expressed as half the product of the hypotenuse \( c \) and the height \( h \) relative to the hypotenuse: $$ A = \frac{1}{2}ch $$ Since both expressions represent the area of the same triangle, we can set them equal: $$ \frac{1}{2}ab = \frac{1}{2}ch $$ Simplifying by canceling \( \frac{1}{2} \) from both sides of the equation and solving for \( h \): $$ ab = ch $$ From which we derive the height (h): $$ h = \frac{ab}{c} $$ This proves that the height \( h \) relative to the hypotenuse is indeed the product of the legs divided by the hypotenuse.
Congruence Criteria for Right Triangles
Right triangles follow some specific congruence criteria:
- Two right triangles are congruent if their legs are congruent
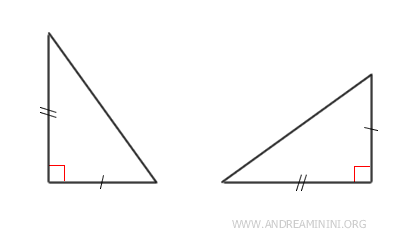
Proof: According to the first congruence criterion (SAS), two triangles are congruent if they have two congruent sides and the included angle is congruent. In a right triangle, the angle between the two legs is always a right angle (90°). Therefore, the congruence criterion for two right triangles reduces to having two congruent legs.
- Two right triangles are congruent if they have one congruent side and one congruent acute angle
Proof: Right triangles have a right angle, so if one acute angle is congruent, the other angle is also congruent because the sum of the internal angles is always 180°. Knowing that one side is congruent, by the second generalized congruence criterion (ASA), the two triangles are congruent.
- Two right triangles are congruent if they have one congruent leg and a congruent hypotenuse
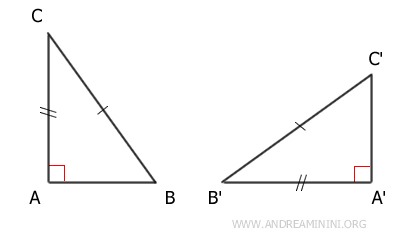
Proof: By the initial hypothesis, two triangles ABC and A'B'C' have a congruent leg AB≅A'B' and congruent hypotenuses BC≅B'C'. Now, I construct a triangle ACD congruent with triangle A'B'C' and sharing the leg AC with triangle ABC.
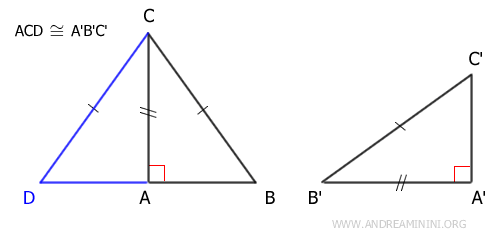
Triangle BCD is an isosceles triangle because it has two congruent sides BC≅CD. As an isosceles triangle, it also has congruent acute angles adjacent to the base β≅γ.
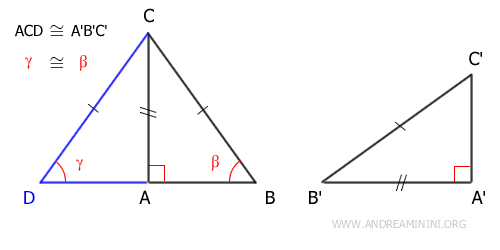
Therefore, by the second generalized congruence criterion (ASA), the two triangles ACD≅ABC are congruent because they share side AC, have congruent sides BC≅CD, and have congruent angles β≅γ. Consequently, knowing that ACD≅A'B'C' are congruent by construction, I can deduce by the transitive property that the triangles ABC≅A'B'C' are congruent.
An Alternative Proof
Let’s consider two right triangles, ABC and A'B'C', both with right angles at vertices B and B'. Suppose one leg is congruent (BC = B'C') and the hypotenuse is also congruent (AC = A'C'). We aim to prove that triangles ABC and A'B'C' are congruent.

Extend segment A'B' by adding a segment B'D such that B'D ≅ AB. Then, connect point D to C', forming triangle B'C'D. Since the angle at B' is supplementary to a right angle, it is itself a right angle, making B'C'D a right triangle as well.

By the first congruence criterion (SAS), triangles ABC and B'C'D are congruent ABC ≅ B'C'D, since they share one congruent side (AB ≅ B'D, by construction), another congruent side (BC ≅ B'C', by assumption), and the included right angle (90°). It follows that AC ≅ C'D.

Triangle A'C'D is isosceles, since it has two equal sides. In an isosceles triangle, the altitude from the apex also serves as the median, so A'B' ≅ B'D.

As a result, triangles A'B'C' ≅ B'C'D are congruent by the third congruence criterion (SSS), since all their sides are equal. Given that ABC ≅ B'C'D and A'B'C' ≅ B'C'D, by transitivity we conclude that ABC ≅ A'B'C', as required.
Right Triangle and Trigonometry
In trigonometry, the right triangle plays a central role.
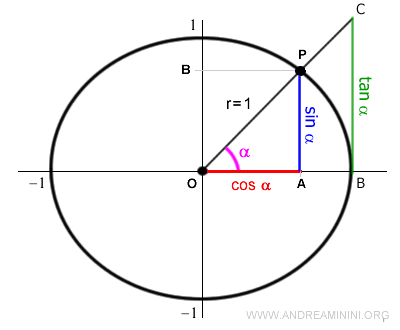
All the main trigonometric functions are, in some way, related to the right triangle.
- Sine
The sine is defined as the ratio of the opposite leg to the hypotenuse: $$ \sin ( \alpha ) = \frac{AP}{OP} $$ - Cosine
The cosine is defined as the ratio of the adjacent leg to the hypotenuse: $$ \cos ( \alpha ) = \frac{OA}{OP} $$ - Tangent
The tangent is defined as the ratio of the opposite leg to the adjacent leg: $$ \tan( \alpha) = \frac{AP}{OA} = \frac{\sin( \alpha )}{\cos( \alpha )} $$
By considering an acute angle in the triangle (other than the right angle), the sides of the triangle can be directly related to these functions.
Trigonometry has countless practical applications
For example, it is used in navigation to calculate distances, in architecture for designing buildings, in electronics for studying waves, and much more.
Thus, the right triangle is perhaps one of the geometric shapes most relevant to our daily lives.
Key Points
Some observations and notes on right triangles.
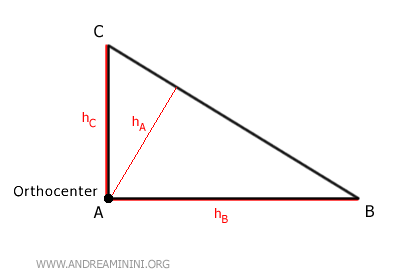
- Orthocenter
In a right triangle, the orthocenter is located at the vertex of the right angle.
- In a right triangle, the acute angles are complementary
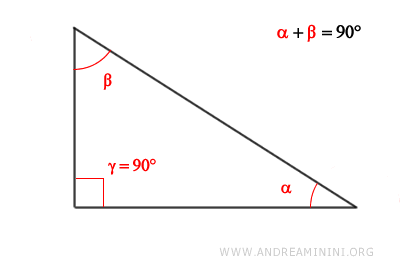
Proof: A right triangle has one right angle (90°). According to the theorem of the sum of the internal angles, the sum of the internal angles of a triangle is 180°. $$ \alpha + \beta + \gamma = 180° $$ Knowing that one angle is a right angle, for example γ = 90°, we have: $$ \alpha + \beta + 90° = 180° $$ $$ \alpha + \beta = 180° - 90° $$ $$ \alpha + \beta = 90° $$ Therefore, the acute angles of the triangle are complementary angles, meaning their sum is equal to a right angle.
- In a right triangle, the median of the hypotenuse is equal to half the hypotenuse
In any right triangle, the length of the median (AM) drawn to the hypotenuse (BC) is exactly half the length of the hypotenuse: (AM ≅ 1/2 BC)
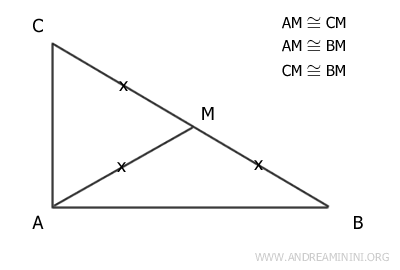
The converse is also true: if, in a triangle, a median measures exactly half the side to which it is drawn, then the triangle must be right-angled.
Proof: Consider a right triangle ABC, the midpoint M of the hypotenuse, and the median to the hypotenuse. It is known that angle α is a right angle (α=90°) and segments BM≅CM are congruent because M is the midpoint of the hypotenuse AB.
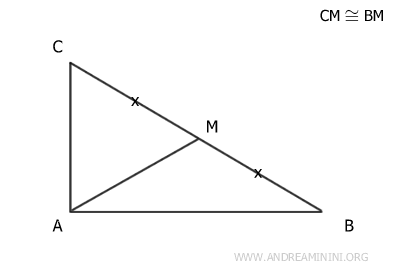
Next, extend segment AM with a congruent segment MD. Then draw segments BD and CD, forming a quadrilateral.
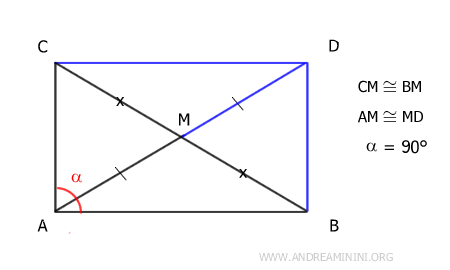
This quadrilateral is a parallelogram because its diagonals AD and BC intersect at their midpoint. Furthermore, knowing that angle α=90° from the initial hypothesis (right triangle), the parallelogram is also a rectangle. In a rectangle, the diagonals are congruent AD≅BC. Therefore, the halves of the segments are also congruent AD/2≅BC/2, meaning AM≅BM and AM≅CM. This proves that in a right triangle, the median to the hypotenuse AM is congruent to half the hypotenuse AM≅BM and AM≅CM.
Alternative Proof. Consider a right triangle, and let M be the midpoint of the hypotenuse (AC). Thus, BM is the median to the hypotenuse.

Now extend the median BM by constructing a segment BD such that BD ≅ BM. Then draw segment AD, forming triangle ABD.

Triangles ADM and BCM are congruent by the first triangle congruence criterion (SAS), since they share two pairs of congruent sides (AM ≅ CM by definition of midpoint, and BD ≅ BM by construction), and the included angles $ \angle AMD $ and $ \angle BMC $ are congruent because they are vertical angles at point M. Since these triangles are congruent, their corresponding angles and sides are equal. In particular, we have $ \alpha' \cong \gamma $.

From triangle ABC, we know that angles $ \alpha $ and $ \gamma $ are complementary: $$ \alpha + \gamma = 90^\circ $$ Since $ \alpha' \cong \gamma $, it follows that $ \alpha + \alpha' = 90^\circ $ as well. Therefore, triangle ABD is a right triangle. Moreover, triangles ABD and ABC are congruent because they share leg AB, and the other legs are congruent (AD ≅ BC). It follows that their hypotenuses are also congruent: $$ AC \cong BD $$ By construction, we also know that $ BD = 2 \, BM $, so: $$ AC \cong 2 \, BM $$ Thus, the median BM is exactly half the length of the hypotenuse AC: $$ BM \cong \frac{1}{2} \, AC $$ as was to be shown.
Proof of the Converse Theorem. Consider a triangle ABC in which the median BM equals half the length of the side AC to which it is drawn.

In other words: $$ BM = \frac{1}{2} \, AC $$ It follows that the segments BM, AM, and CM are congruent: $$ BM \cong AM \cong CM $$ As a result, triangles ABM and CBM are isosceles, each having two equal sides (BM ≅ AM and BM ≅ CM). Therefore, the base angles of triangles ABM and CBM are congruent.

Since the sum of the interior angles of any triangle is always 180°, the angles in triangle ABC satisfy: $$ \alpha + \gamma + (\alpha + \gamma) = 180^\circ $$ which simplifies to: $$ 2\alpha + 2\gamma = 180^\circ $$ Dividing both sides by 2 gives: $$ \alpha + \gamma = 90^\circ $$ Thus, the remaining angle in triangle ABC is a right angle. It follows that triangle ABC is a right triangle - as required. - The case of the right triangle with acute angles of 30° and 60°
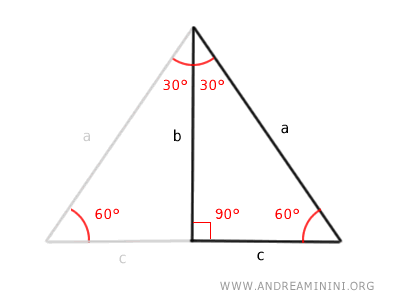
A right triangle with acute angles of 30° and 60° is half of an equilateral triangle. This allows the calculation of the lengths of all sides of the triangle based on the length of one side. $$ a = \frac{2b}{\sqrt{3}} $$ $$ b = \frac{a}{2} \sqrt{3} $$ $$ c = \frac{a}{2} $$ These formulas apply only to triangles with internal angles of 30°, 60°, and 90°. - The case of the right triangle with two acute angles of 45° (isosceles right triangle)
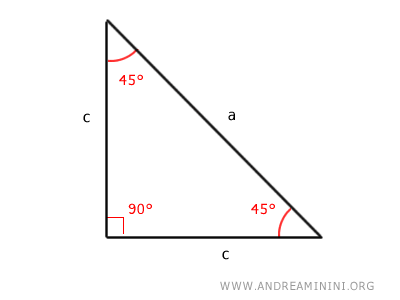
This particular type of right triangle is also an isosceles triangle because it has two congruent legs. This allows the calculation of the lengths of all sides of the triangle based on one side. $$ c = \frac{a}{ \sqrt{2} } $$ $$ a = c \cdot \sqrt{2} $$ These formulas apply only to triangles with two acute angles of 45°. - Two right triangles are similar if their legs are proportional
According to the second similarity criterion for triangles, two triangles are similar if their sides are proportionally equal, and the included angle is congruent.

In right triangles, the angle between the legs is always a right angle (90°), so it is congruent. Therefore, if the legs are proportional, by the second similarity criterion, the two triangles are similar triangles, meaning they have all congruent angles and the same shape, but possibly different sizes and orientations. - Two right triangles with one congruent acute angle are similar
The sum of the internal angles of a triangle is always 180°. $$ \alpha + \beta + \gamma = 180° $$ Knowing that in two right triangles the right angle is 90°, if they also have one congruent acute angle, then by difference the third angle is also congruent. Therefore, the two triangles have all congruent angles, and according to the first similarity criterion for triangles, the two triangles are similar.
And so on.
