First Criterion for Similarity in Triangles
Two triangles are deemed similar when they share two corresponding congruent angles.
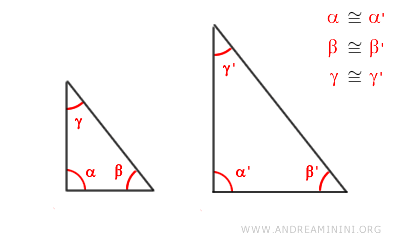
When two triangles have pairs of internal angles that match in congruence, it logically follows that the third angle of each triangle must also be congruent.
This stems from the fundamental principle that the sum of a triangle's internal angles always equals 180 degrees.
$$ \alpha + \beta + \gamma \cong 180° $$
Hence, with two pairs of angles in congruence, the third pair must naturally be congruent as well.
Thus, the triangles are similar because they preserve the same angular sequence, demonstrating identical shapes albeit with potential size variations.
$$ ABC \approx A'B'C' $$
This is commonly referred to as the AAA (Angle-Angle-Angle) Similarity Criterion among triangles.
An Illustrative Example
Consider the triangles ABC and A'B'C'
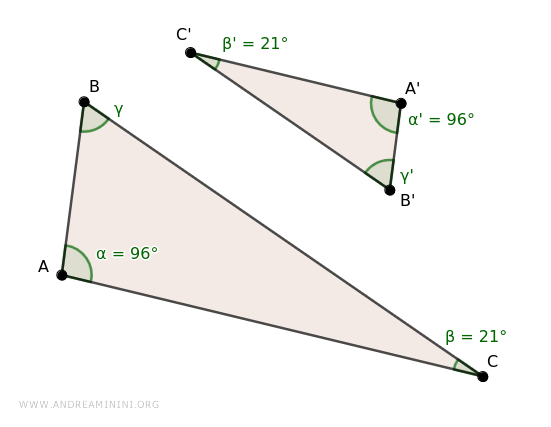
The angle pairs α≅α' (96°) and β≅β' (21°) are congruent.
Given the universal truth that the sum of the internal angles in a triangle is 180°
$$ \alpha + \beta + \gamma = 180° $$
$$ \alpha ' + \beta ' + \gamma ' = 180° $$
We can deduce the measures of angles γ and γ' from the known angles.
$$ \gamma = 180° - \alpha - \beta $$
$$ \gamma ' = 180° - \alpha ' - \beta ' $$
With α≅α'≅96° and β≅β'≅21°,
$$ \gamma = 180° - 96° - 21° $$
$$ \gamma ' = 180° - 96° - 21° $$
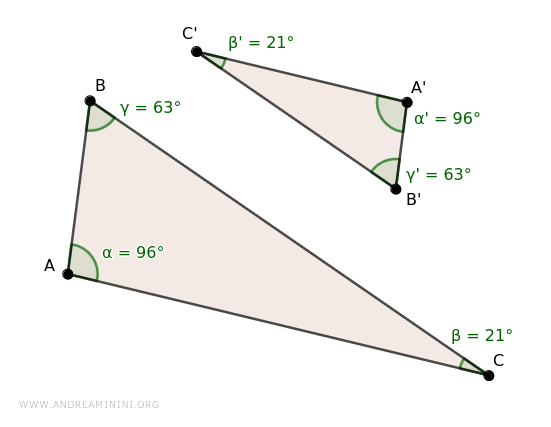
Thus confirming that γ and γ' are congruent as they result from the algebraic sum of congruent angles.
$$ \gamma = 63° $$
$$ \gamma ' = 63° $$
Triangles ABC and A'B'C' share congruent angles α≅α' (96°), β≅β' (21°), and γ≅γ' (63°), making them similar.
Proving Similarity
Let's delve into triangles ABC and A'B'C'
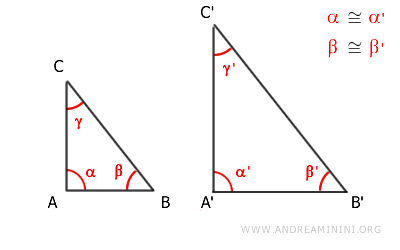
Starting with the premise that corresponding angles α≅α' and β≅β' are congruent,
$$ \alpha \cong \alpha ' $$
$$ \beta \cong \beta ' $$
Our goal is to demonstrate the similarity between triangles ABC and A'B'C'.
This involves examining the congruence of segments between corresponding angles, specifically segments AB and A'B'.
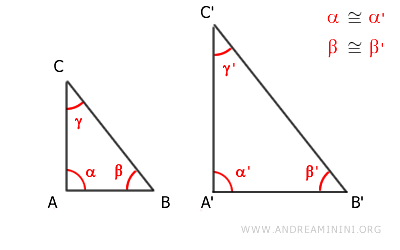
1) Congruence of Segments AB and A'B'
If segments AB and A'B' are congruent, then triangles ABC and A'B'C' are congruent by the second criterion of triangle congruence.
Consequently, congruent geometric figures are inherently similar, with a similarity ratio of 1, proving similarity in this scenario.
2) Non-Congruence of Segments AB and A'B'
If segments AB and A'B' are not congruent, we calculate the ratio k between them:
$$ k = \frac{\overline{A'B'}}{\overline{AB}} $$
Next, we apply a homothety to triangle ABC with center C and a similarity ratio of k=A'B'/AB.
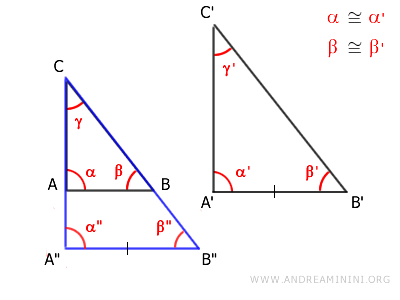
By design, segments A"B"≅A'B' are congruent as both A'B'=k·AB and A"B"=k·AB.
$$ \overline{A''B''} \cong \overline{A'B'} $$
Moreover, homothety ensures parallelism between segments, confirming A"B" and AB are parallel.
$$ \overline{A''B''} \ || \ \overline{AB} $$
Using the parallel lines theorem, it follows that angles α≅α" and β≅β" are congruent as corresponding angles formed by transversals intersecting parallel lines AB || A"B".
$$ \alpha \cong \alpha '' $$
$$ \beta \cong \beta '' $$
Given the initial congruences of β≅β' and α≅α', it follows that α'≅α" and β'≅β" are congruent.
$$ \alpha ' \cong \alpha '' $$
$$ \beta ' \cong \beta '' $$
Therefore, by the criteria for triangle congruence, triangles A"B"C and A'B'C' are congruent, establishing their similarity as A'B'C' is congruent to a homothetic triangle of ABC.
3) Final Thoughts
In summary, whether or not AB and A'B' are adjacent, the triangles ABC and A'B'C' are proven similar, validating the first criterion of triangle similarity.
Thus, we have a comprehensive demonstration of triangle similarity.
And so forth.
