Theorem of Circumscribed Circle Radius for Similar Regular Polygons
For any two regular polygons with an identical number of sides that are similar, not only are all their sides proportional, but the radii of their circumscribed circles and their apothems also maintain the same proportionality as the sides.
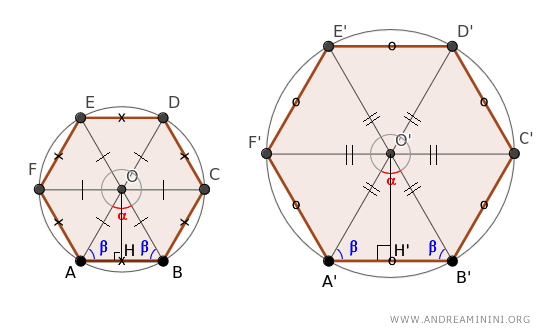
This theorem confirms that when dealing with two similar regular polygons that share the same number of sides, there’s a consistent ratio not just between their sides, but also between the radii of their encompassing circles and their apothems.
In other words, the proportional relationship between the sides of the two polygons is also mirrored in the ratio of the radii of the circumscribed circles to each polygon and their apothems.
Corollary. Since two regular polygons with the same number of sides also exhibit their perimeters in the same proportion (see the perimeter theorem for similar polygons), it follows that the radii of the circumscribed circles and the apothems are in the same ratio as the corresponding sides and the perimeters of the two similar polygons.
Illustrative Example
Consider two similar regular hexagons as an example.
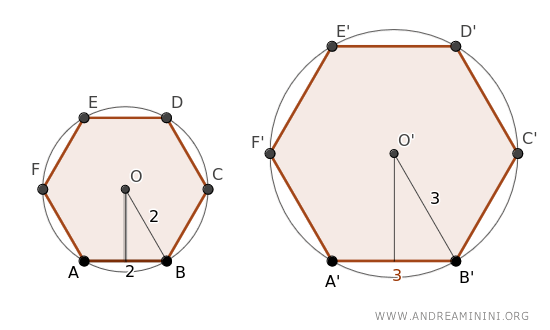
The first hexagon has sides of length 2, while the second has sides of length 3.
$$ AB = BC = CD = DE = EF = AD = 2 $$
$$ A'B' = B'C' = C'D' = D'E' = E'F' = A'D' = 3 $$
Being regular polygons, both can be enclosed by a circle, with radii of 2 and 3, respectively.
$$ OB = 2 $$
$$ O'B' = 3 $$
It becomes immediately apparent that the radii are to the corresponding sides as 2 is to 3
$$ OB : O'B' = AB : A'B' $$
$$ 2 : 3 = 2 : 3 $$
$$ 0.6666 = 0.6666 $$
Here, the proportionality ratio consistently repeats as 0.6666.
To determine the apothems, we calculate the legs of the right-angled triangles OBH and O'B'H' employing the Pythagorean theorem.
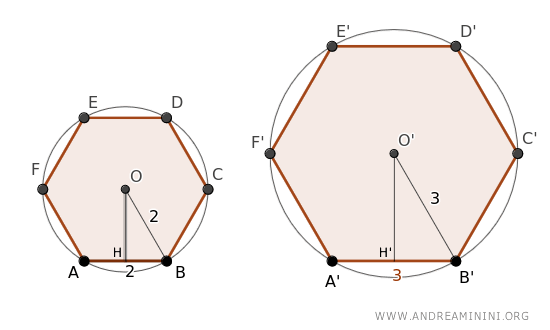
The right triangles have sides OB=2 and HB=1, and O'B'=3 and H'B'=1.5
$$ OH = \sqrt{2^2 - 1^2} = \sqrt{3} $$
$$ O'H' = \sqrt{3^2 - 1.5^2} = \sqrt{6.75} $$
The legs OH and O'H' represent the apothems of the two hexagons.
Finally, we compute the ratio between these legs.
$$ \frac{ \sqrt{3} }{ \sqrt{6.75} } = 0.6666 $$
The proportionality ratio among the apothems mirrors that of the circumcircle radii and the corresponding sides of the polygons.
Proving the Theorem
Let's take two regular polygons with the same number of sides as our subjects.
Imagine, for instance, two hexagons of differing sizes.
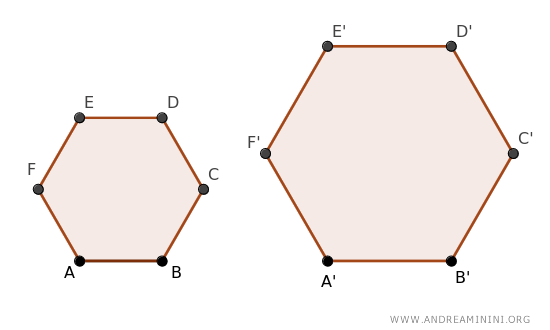
As regular polygons with identical sides, they are considered similar by the theorem of similarity for regular polygons.
Since they're similar, all sides maintain a uniform ratio.
$$ AB:A'B' = BC:B'C' = CD:C'D' = DE:D'E' = EF:E'F' = AF:A'F' $$
Moreover, as regular polygons, they can each be circumscribed by a circle.
Draw lines from the center O to every vertex of the hexagons.
These lines are equal within each polygon since they match the radius of the circle they describe.
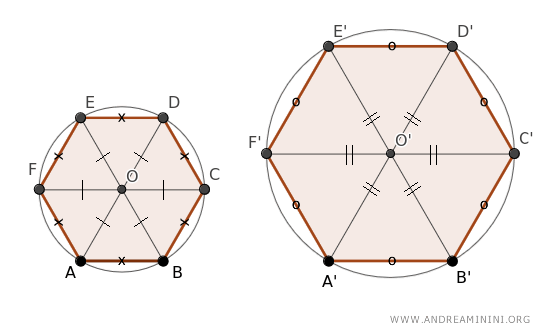
This action divides each hexagon into six triangles.
All these triangles are isosceles because the sloped sides are equal to the radius of their respective circle.
Furthermore, according to the third criterion for triangle congruence, the triangles within each polygon are congruent since their sides are identically matched.
$$ ABO \cong BCO \cong CDO \cong EDO \cong EFO \cong AFO $$
$$ A'B'O' \cong B'C'O' \cong C'D'O' \cong E'D'O' \cong E'F'O' \cong A'F'O' $$
Also, in both polygons, the central angle is divided into six equal segments.
$$ \alpha = \frac{360°}{6} = 60° $$
Thus, every triangle in both polygons shares a vertex angle at O (α=60°).
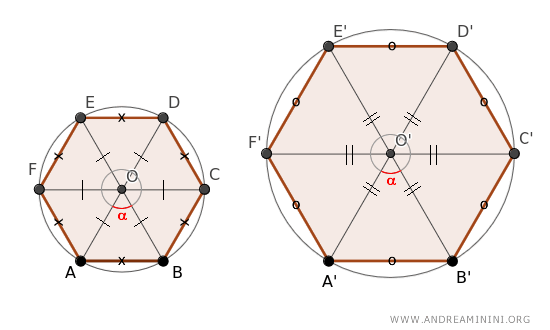
By employing the second criterion of triangle similarity, the triangles in the first polygon are similar to those in the second, as they have one congruent angle and sides in proportion.
Focusing solely on the triangles ABO and A'B'O' for simplicity:
$$ ABO \approx A'B'O' $$
This establishes that all sides of the two triangles are proportional.
$$ AB:A'B' = OB:O'B' = OA:O'A' $$
Where AB and A'B' represent the sides of the polygons, while OA and O'A' denote the radii of the circle.
This proves that the radii of the circumscribed circles are to the sides of the regular polygons in the same proportion.
Note. The triangles ABO and A'B'O' are similar isosceles triangles, meaning all their sides are in proportion. Consequently, the heights relative to their bases AB and A'B', i.e., the apothems of the polygons, are also proportional. $$ OH:O'H' = OA:O'A' = AB:A'B' $$
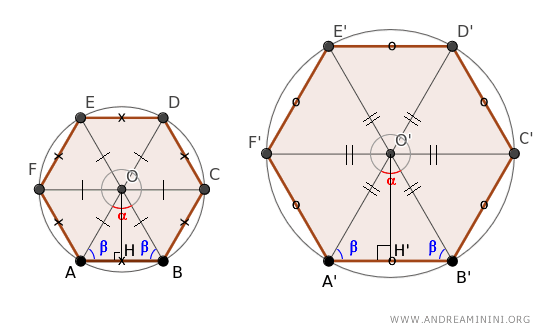
To verify this, consider that isosceles triangles have congruent base angles. Since the vertex angle is congruent (α) the triangles ABO and A'B'O' also have congruent base angles $$ \beta = \frac{ 180° - α }{2} $$ Hence, if we divide the two isosceles triangles into two right triangles AOH and A'O'H, these are also similar because, by the second criterion of similarity of triangles, they have two sides in proportion OA:O'A'=AH:A'H' and the angle β between them congruent. Therefore, the height is also proportional. $$ OH:O'H' = OA:O'A' $$ This proves that the apothem of the polygon has the same proportional relationship as the radius of the circumcircle and the side of the polygon.
And so on.
