Apothem
The apothem of a regular polygon is the line segment that connects the center of the polygon to the midpoint of one of its sides, forming a right angle with that side.
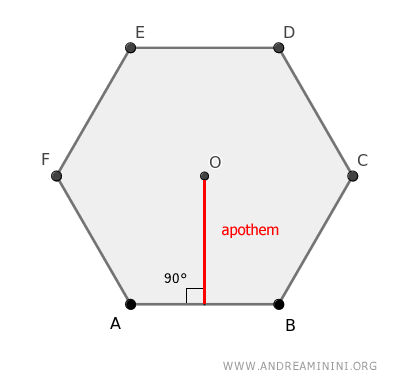
In simpler terms, the apothem is the distance from the center of the polygon to one of its sides.
In regular polygons, the apothem also represents the radius of the circle inscribed within the polygon, known as the inradius.
The Relationship Between the Apothem and the Side Length of a Regular Polygon
The ratio between the apothem (a) and the side length (l) is a constant for a given polygon and is referred to as the polygon’s "fixed number" (or constant f). $$ f = \frac{a}{l} $$ This constant varies depending on the number of sides the polygon has.
The fixed number remains the same regardless of the polygon’s size or the length of its sides.
Each type of polygon has its own unique fixed number.
For example, in a pentagon, the fixed number is always the non-terminating, non-repeating decimal 0.688... For calculations, we typically use the approximated value 0.688. In a hexagon, the fixed number is approximately 0.866.
Here’s a table with the f constants for some common polygons:
| Polygon | Constant f |
|---|---|
| Equilateral Triangle | 0.289... |
| Square | 0.5 |
| Pentagon | 0.688... |
| Hexagon | 0.866... |
| Heptagon | 1.038... |
| Octagon | 1.207... |
| Nonagon | 1.374... |
| Decagon | 1.539... |
| Dodecagon | 1.866... |
Why is it important to know the f constants?
Knowing the f constant allows you to calculate the side length if you know the apothem $$ l = \frac{a}{f} $$ or calculate the apothem if you know the side length $$ a = l \cdot f $$
For example, consider a hexagon with each side measuring 6 cm.
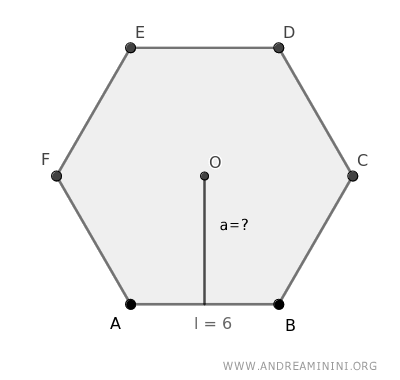
You can calculate the apothem (a) knowing that the fixed number for any regular hexagon is approximately f = 0.866 $$ a = l \cdot f $$ $$ a = 6 \cdot 0.866 $$ $$ a = 5.196 $$
The f constant is also very useful when calculating the area of a regular polygon.
$$ A = n \cdot \frac{l \cdot a}{2} $$
Since the apothem is equal to the product of the side length (l) and the f constant, you can substitute a = l·f into the previous formula
$$ A = n \cdot \frac{l \cdot l \cdot f}{2} $$
$$ A = n \cdot \frac{l^2 \cdot f}{2} $$
The product of half the number of sides of the polygon and the f constant is known as the φ constant (pronounced "phi").
$$ \phi = \frac{n \cdot f}{2} $$
This is another constant that depends on the f constant and varies based on the number of sides of the polygon.
Thus, you can also rewrite the formula for the area of a regular polygon as the product of the square of the side length and the φ constant:
$$ A = l^2 \cdot \phi $$
Here are some approximate values for the φ constants:
| Polygon | Constant φ |
|---|---|
| Equilateral Triangle | 0.433... |
| Square | 1 |
| Pentagon | 1.72... |
| Hexagon | 2.598... |
| Heptagon | 3.634... |
| Octagon | 4.828... |
| Nonagon | 6.182... |
| Decagon | 7.694... |
| Dodecagon | 11.196... |
Note: The inverse formulas are also very useful for working with the φ constant. For example, you can calculate the side length (l) if you know the area (A) of the regular polygon $$ l = \sqrt{ \frac{A}{ \phi } } $$ This formula is derived by solving for the side length from the area formula $$ A = l^2 \cdot \phi $$ $$ l^2 = \frac{A}{ \phi } $$ $$ \sqrt{l^2} = \sqrt{ \frac{A}{ \phi } } $$ $$ l = \sqrt{ \frac{A}{ \phi } } $$
And so on.
