Rectangle
A rectangle is a type of parallelogram where all angles are congruent and right angles.
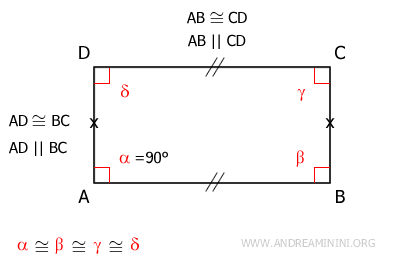
As with any parallelogram, a rectangle has the following properties:
- Opposite sides are congruent and parallel
- Opposite angles are congruent
- Adjacent angles along one side are supplementary
- Diagonals intersect at their midpoint
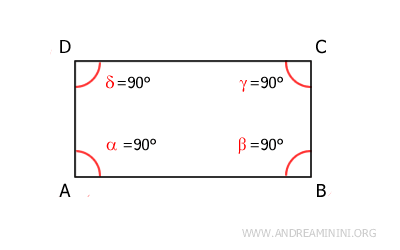
Additionally, each angle in a rectangle is a right angle (90°).
Being a quadrilateral, the sum of the interior angles of a rectangle is 360°. Given that all angles in a rectangle are congruent, each angle must be a right angle (90°), as 360° divided by four equals 90°.
In a rectangle, the diagonals are congruent, meaning they are equal in length.
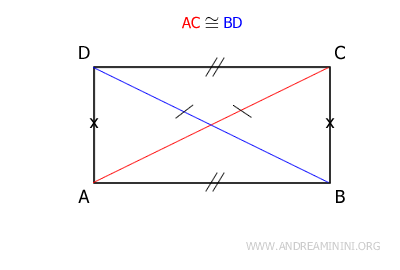
Each diagonal divides the rectangle into two congruent right triangles.
Furthermore, the diagonals divide the rectangle into four isosceles triangles, which are congruent in pairs.
Key Formulas for a Rectangle
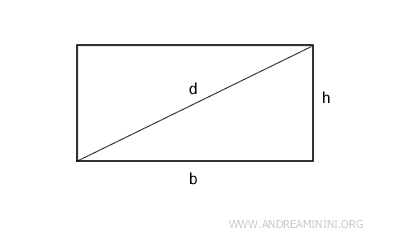
- The perimeter of a rectangle is twice the sum of the base and height: $$ P = 2 \cdot (b + h ) $$
- The area of a rectangle is the product of the base and height: $$ A = b \cdot h $$ See the proof.
- The diagonal is the square root of the sum of the squares of the base and height, derived from the Pythagorean theorem: $$ d = \sqrt{b^2 + h^2} $$
The Base and Height of a Rectangle
The base and height of a rectangle are also known as its dimensions.
In a rectangle, any side can be considered the base, with the adjacent side serving as the height.
For instance, in rectangle ABCD, segment AB can be the base, with the adjacent side BC (or AD) as the height.
Alternatively, in the same rectangle, you could consider BC as the base and the adjacent side CD (or AB) as the height.
Additional Notes
Some observations and key points about rectangles:
- A rectangle has congruent diagonals
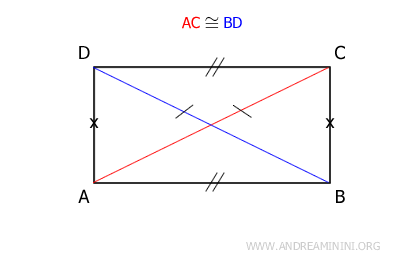
Proof. A rectangle is a parallelogram, so it has congruent opposite sides and angles (AB≅CD and AD≅BC). Additionally, all angles are congruent and are right angles.
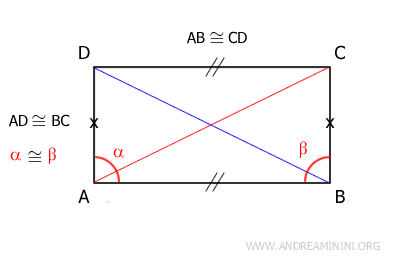
Therefore, by the first congruence criterion for triangles, triangles ABD and ABC are congruent because they have congruent sides (AB≅CD and AD≅BC) and the angle between them is congruent (α≅β). Since these two triangles are congruent, their respective hypotenuses (AC≅BD), which are the diagonals of the rectangle, are also congruent. - Each diagonal divides the rectangle into two congruent right triangles
Proof. A rectangle has congruent opposite sides and right angles, which is sufficient to establish the congruence of the two triangles formed by any diagonal. For example, diagonal AC divides the rectangle into two triangles, ABC and ACD.
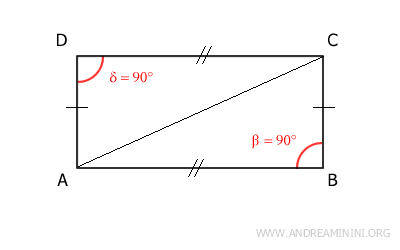
These two triangles share a side (AC) and have congruent sides (AD≅BC and AB≅CD). Therefore, by the third congruence criterion (SSS), these triangles are congruent. Since they both have a right angle, they are also right triangles. The same logic applies to the other diagonal, BD, of the rectangle. - The diagonals divide the rectangle into four isosceles triangles, congruent in pairs
Proof. A rectangle has congruent opposite sides, congruent diagonals, and right angles. Being a parallelogram, the diagonals (AC≅BD) intersect at their midpoint M, so the halves of the diagonals are also congruent (AM≅CM≅BM≅DM).
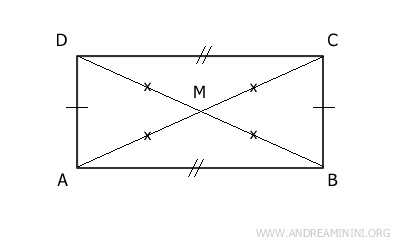
The diagonals divide the rectangle into four triangles. Taken in pairs, by the third congruence criterion (SSS), the opposite triangles AMD≅BMC and ABM≅CDM are congruent because they have three congruent sides in the same order. Additionally, all four triangles have congruent oblique sides, as they coincide with the halves of the diagonals (AM≅CM≅BM≅DM) of the rectangle. Therefore, the four triangles are isosceles triangles. - A parallelogram is a rectangle if at least one of its angles is a right angle
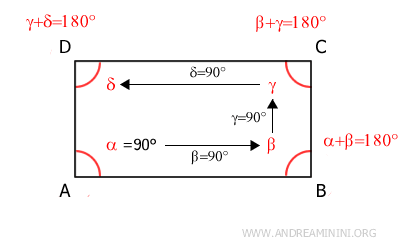
If one angle of a parallelogram is a right angle (90°), then all the other angles must also be right angles. Therefore, the parallelogram is a rectangle.Proof. In a parallelogram, the adjacent angles along one side are supplementary angles (180°). Thus, if one angle measures 90° (a right angle), the adjacent angle on the same side must also measure 90°, since supplementary angles add up to 180°=90°+ 90°. Applying this reasoning to each angle, it can be shown that all the angles of the rectangle are right angles.
- A parallelogram is a rectangle if its diagonals are congruent
Proof. Given that the parallelogram ABCD has congruent diagonals (AC≅BD), we can show that this condition is sufficient to conclude that ABCD is a rectangle.
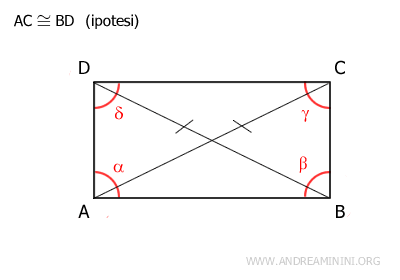
Since ABCD is a parallelogram, it has congruent opposite sides (AB≅CD and BC≅AD).
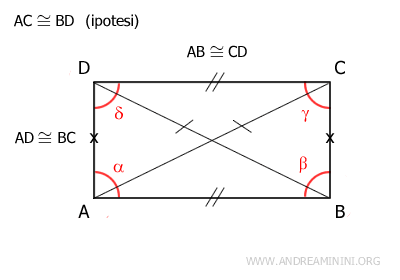
Therefore, by the third congruence criterion, triangles ABC and ABD are congruent, meaning ABC≅ABD, since they have all sides congruent in the same order. Consequently, these triangles have all angles congruent in the same order. Particularly, the angles α≅β are congruent. Knowing that in a parallelogram, adjacent angles along one side are supplementary α+β=180°, and since these angles are congruent α≅β, it follows that each angle is a right angle α=90° and β=90°. Once it’s proven that one angle of the parallelogram is a right angle, it follows that all the other angles are also right angles. This proves that the parallelogram is a rectangle.
And so on...
