Equivalent Polygons

Two polygons are called equivalent polygons when they have the same area.

The key characteristic of equivalent polygons is that they share the same area.

Equivalent polygons can vary in shape and size. They can be regular, irregular, convex, concave, and so on.

 

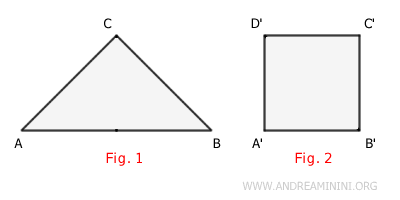
What matters is that their areas are equal, meaning they cover the same amount of surface on a plane.

Note: The concept of equivalence between two polygons is also known as equi-extension.

This means that two equivalent polygons are also equicomposable polygons.

In other words, you can divide the polygons into smaller parts where each part of one polygon is congruent to a part of the other, and vice versa.

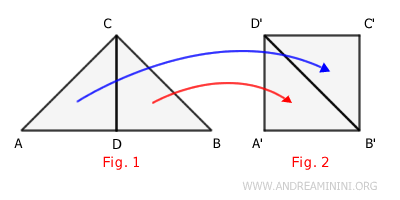
This allows for interesting practical and theoretical applications, such as calculating complex areas by breaking them down into simpler figures.

Using techniques like cutting and rearranging, one polygon can be transformed into another equivalent polygon.

This concept is often illustrated by the Bolyai-Gerwien theorem, which states that any polygon can be transformed into any other equivalent polygon through a finite number of cuts and rearrangements.

Equivalence Criteria

In geometry, there are several criteria for equivalence to determine if two polygons are equivalent without calculating the area.

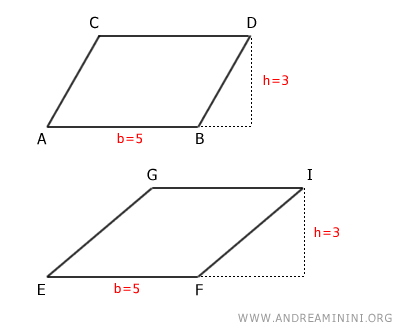
• Parallelogram Equivalence Theorem
  Two parallelograms are equivalent if they have the same base and height.
  
• Triangle Equivalence Theorem
  Two triangles are equivalent if they have the same base and height.
  
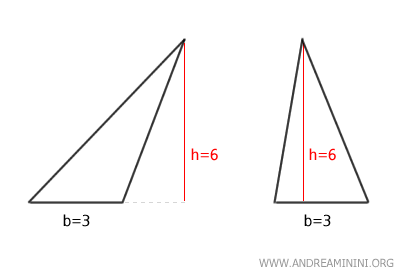
• Equivalence Theorem between a Triangle and a Parallelogram
  A triangle is equivalent to a parallelogram with the same height and a base that is half the base of the triangle.
  
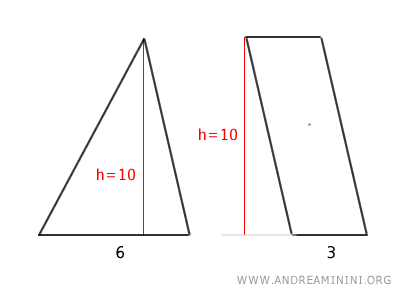
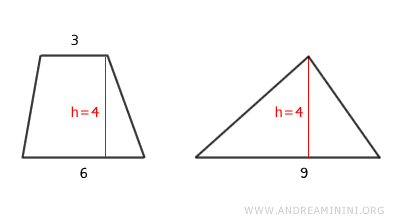
• Equivalence Theorem between a Triangle and a Trapezoid
  A trapezoid is equivalent to a triangle with the same height and a base equal to the sum of the trapezoid's bases.
  
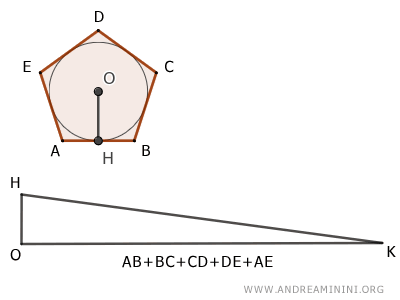
• Equivalence Theorem between a Triangle and a Circumscribed Polygon
  A polygon circumscribed around a circle is equivalent to a triangle with a height equal to the radius of the circle and a base equal to the perimeter of the polygon.
  

  The Case of Regular Polygons: Since all regular polygons can be circumscribed around a circle, it follows that all regular polygons are equivalent to a triangle with a height equal to the radius and a base equal to the perimeter of the polygon.

These are just a few of the equivalence criteria that can be applied to plane geometric figures.

Equivalence and Equidecomposability

In general, two equivalent polygons are also equidecomposable, but the reverse is not necessarily true.

The concept of equivalence in geometry is much broader and not limited to area. It can also apply to volume.

Two plane or solid figures are "equivalent" when they have the same measure, regardless of their shape.

• For plane figures (e.g., polygons), the measure is the area, i.e., their surface extent.
• For solids (e.g., polyhedra), the measure is the volume they occupy in space.

This is important to remember because it implies that equivalence does not always mean equidecomposability.

Example: Two equivalent polygons can be divided and reassembled to transform one into the other while maintaining the same area. However, in the case of equivalent polyhedra sharing the same volume, it is not guaranteed that two solids with the same volume can be decomposed and rearranged to recreate each other's shape.

Observations

Some observations and additional notes:

• Bolyai-Gerwien Theorem
  This theorem states that any polygon can be decomposed and recomposed into an equivalent polygon through a finite number of cuts and rearrangements.
• Equivalent Polygon with One Less Side
  Any convex polygon can be decomposed and recomposed into an equivalent polygon with one less side.
• Equivalent Triangle
  Any convex polygon can be transformed into an equivalent polygon with one less side. By repeatedly applying this principle, it follows that any convex polygon with n>3 sides can be reduced to an equivalent triangle with the same surface area.

And so on.