Kite

A kite (deltoid) is a quadrilateral with two pairs of consecutive sides that are equal in length. It can be either concave or convex.

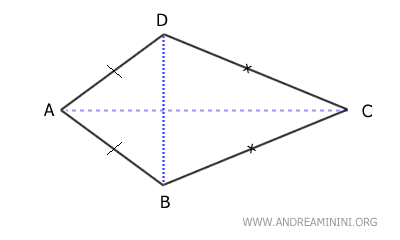
In a kite, two pairs of consecutive sides are congruent, meaning they have the same length, and one pair of opposite angles are equal.

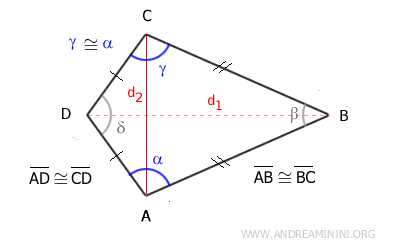
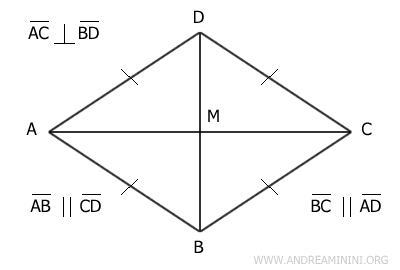
The diagonals of a kite are perpendicular, and one diagonal bisects the other, dividing it into two equal segments.

For example, in the previous figure, diagonal AC is bisected by the other diagonal into two congruent segments. The diagonals are perpendicular to each other. The opposite angles α and γ are congruent, meaning they have the same measure. The consecutive sides AD and CD, as well as AB and BC, are congruent.

To recap, a kite has the following properties:

• One diagonal bisects the angles.
• The diagonals are perpendicular, with one diagonal split into two congruent segments.
• Two opposite angles are congruent.
• It has a line of symmetry that passes through two of its opposite vertices.

Types of Kites

There are two types of kites:

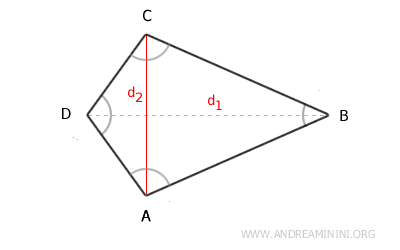
• Convex Kite
  A convex kite has all its angles less than 180°. Both diagonals lie entirely within the polygon.
  
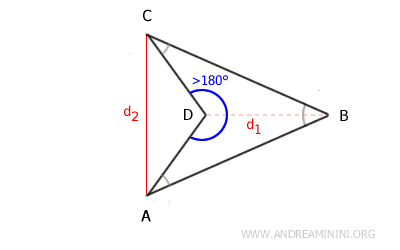
• Concave Kite
  A concave kite has at least one angle greater than 180°. One of its diagonals extends outside the polygon.
  

Formulas

Key formulas for a convex kite:

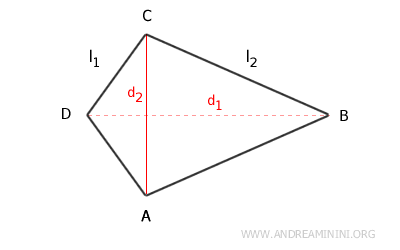
• Area
  The area of a kite is half the product of its diagonals: $$ A = \frac{d_1 \cdot d_2}{2} $$ where d₁ and d₂ are the lengths of the diagonals.
• Perimeter
  The perimeter of a kite is the sum of its sides: $$ P = 2 \cdot l_1 + 2 \cdot l_2 $$

Additional Notes

Some important points to note about kites:

• The rhombus is a special case of a convex kite
  A rhombus is a specific type of convex kite where all sides are congruent, and it has two perpendicular axes of symmetry.
  
• The kite is different from the rhomboid
  A rhomboid is generally a parallelogram without any special properties, with consecutive sides that are not congruent.
  
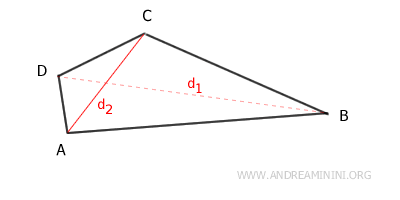
• Differences Between a Kite and a Deltoid
  While a kite is sometimes also called a deltoid or a dart, there are some important distinctions to be aware of.  The distinctions in terminology are important, especially in different mathematical contexts, to avoid confusion between these related but distinct concepts. Let's break down the details:
  • Kite: In elementary geometry, a kite is a quadrilateral with two pairs of adjacent sides that are equal in length. It's a common term used in schools and basic geometric studies. When the kite is not convex, it is sometimes referred to as a "dart."
  • Deltoid: While "deltoid" is often used interchangeably with "kite" to describe this quadrilateral, the term can also refer to a different mathematical object known as a "deltoid curve" (or tricuspoid), which is a type of hypocycloid curve. This curve is unrelated to quadrilaterals but shares the same name due to its delta-like shape.
  • Dart: A kite is typically convex, meaning all its interior angles are less than 180°. However, when a kite is concave, meaning it has one interior angle greater than 180°, it is often referred to as a dart. This usage emphasizes the non-convex nature of the shape.

And so on.