Reducing the Number of Sides in Convex Polygons

A convex polygon can always be made equivalent to a polygon with fewer sides, while keeping the same area.

The principle is based on the idea that you can reduce the number of sides of a polygon through decomposition and rearrangement.

The exception to this rule is, of course, the triangle, since there’s no such thing as a polygon with just two sides. By definition, a polygon must have at least three sides.

This concept is particularly useful for showing that, in plane geometry, changing a polygon's shape doesn’t affect its area.

Note: This method can be applied to both convex and concave polygons, though it's much simpler and more intuitive for convex ones. For concave polygons, the process might involve more complex cuts and rearrangements to account for indentations.

How to Create an Equivalent Polygon with Fewer Sides

There are several methods to reduce the number of sides of a polygon.

One approach involves breaking the polygon down into smaller polygons and reassembling them into a different shape.

One of the simplest methods uses the diagonals of the polygon.

Let’s take any polygon, whether regular or irregular. In this case, we’ll use a hexagon as an example.

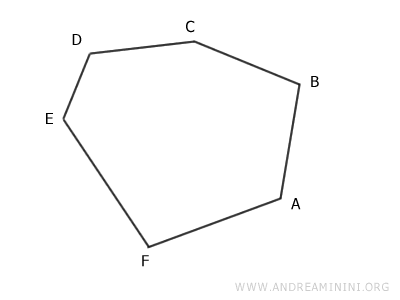
Start by drawing a diagonal between two points that have a point in between.

For example, draw the diagonal from point A to point C, with point B in between.

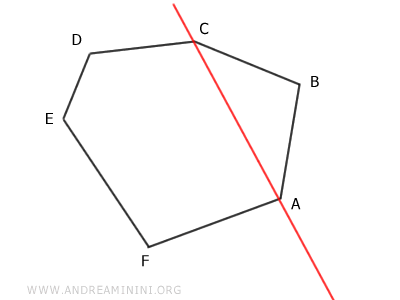
Next, shift the diagonal so that it passes through the intermediate point B.

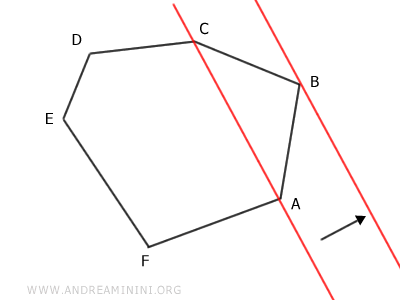
Then, extend one of the segments ending at A or C until it intersects the diagonal.

For instance, extend segment AF until it meets point A'.

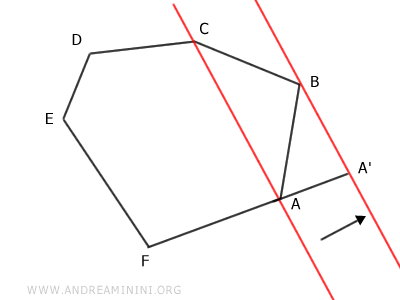
Finally, draw a new segment from A' to C, effectively eliminating vertex B from the polygon.

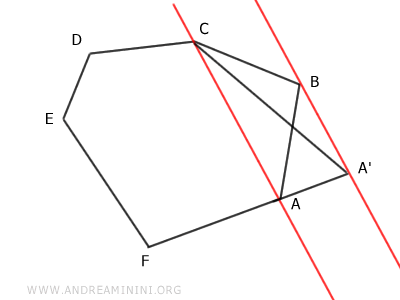
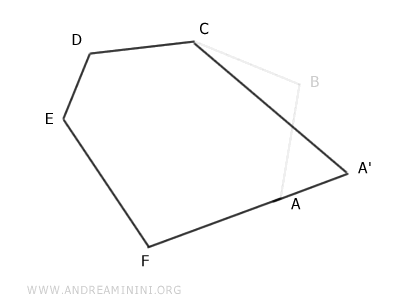
The result is a polygon A'CDEF with five sides, forming a pentagon.

This pentagon is equivalent to the original hexagon, meaning it has the same area.

Proof: To prove this, observe the triangles AA'C and ABC.

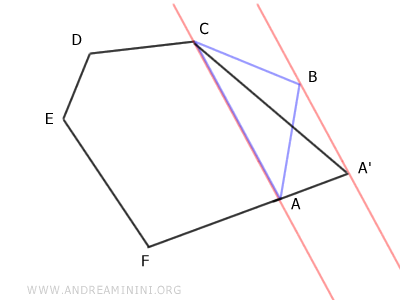
These two triangles share the same base (AC) and have the same height (AA' ≅ BB'). Therefore, according to the triangle congruence theorem, they are equivalent, meaning they have the same area.

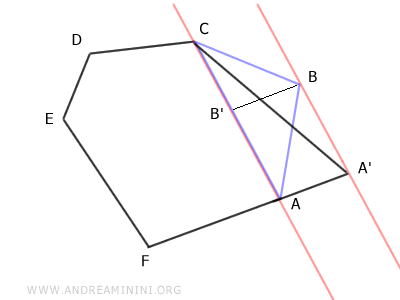
From here, it's easy to see that the hexagon is made up of the polygon ACDEF plus the triangle ABC: $$ ABCDEF \equiv ACDEF + ABC $$ The pentagon A'CDEF is made up of the polygon ACDEF plus the triangle AA'C: $$ A'CDEF \equiv ACDEF + AA'C $$ Since triangles ABC and AA'C are equivalent, both the hexagon and the pentagon are equidecomposable polygons, meaning they consist of the same equivalent polygons. $$ ABCDEF \equiv ACDEF + ABC \equiv ACDEF + AA'C \equiv A'CDEF $$ $$ ABCDEF \equiv A'CDEF $$ Thus, the hexagon ABCDEF and the pentagon A'CDEF are equivalent.

By repeating this process, you can further reduce the pentagon A'CDEF to an equivalent quadrilateral C'DEF (4 sides).

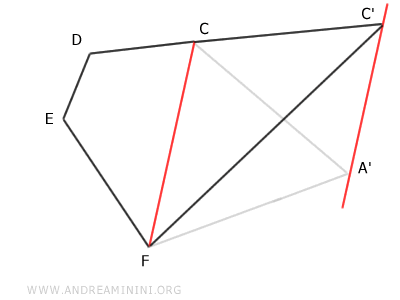
Finally, you can reduce the quadrilateral C'DEF to an equivalent triangle C'D'F (3 sides).

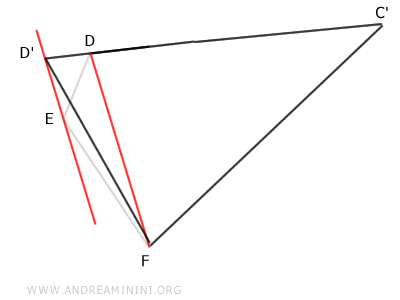
From this, we can deduce that any convex polygon can be reduced to an equivalent triangle.

Note: The method I’ve described for reducing the number of sides using diagonals is not a standard approach in Euclidean geometry. In practice, changing the number of sides in a polygon while keeping the same area generally involves more complex decomposition and rearrangement techniques than simply drawing or shifting diagonals.

Additional Remarks

Here are some additional observations and notes:

• Concave Polygons
  For concave polygons, reducing the number of sides while preserving the area isn’t always possible within Euclidean geometry.

And so on.