The Golden Rectangle

The Golden Rectangle is a geometric shape renowned for its unique property: the ratio of its longer side (the length) to its shorter side (the width) equals the golden ratio, approximately 1.618. $$ \frac{ \text{long side} }{ \text{short side} } = 1.618 $$

This ratio is also known as the golden section.

The number 1.618 (approximated) is referred to as the golden number.

$$  φ = 1.618033988749895   $$

For instance, this rectangle is a golden rectangle.

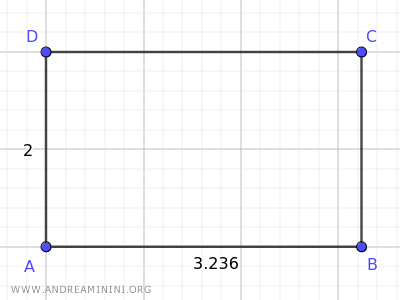
It's evident that the ratio between the longer side (AB) and the shorter side (AD) is roughly equal to the golden number (1.618).

$$ \frac{ \overline{AB} }{ \overline{AD} } = \frac{3.236}{2} = 1.618 $$

What makes the golden rectangle unique is that if you remove a square whose side is equal to the rectangle's shorter side, the remaining rectangle is also golden.

For example, the rectangle BCFE is also a golden rectangle.

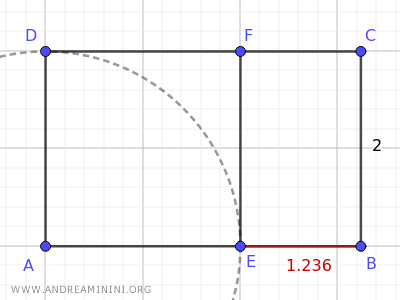
The ratio between the longer side (2) and the shorter side (1.236) is still approximately equal to the golden number (1.618).

$$ \frac{ \overline{BC} }{ \overline{EB} } = \frac{2}{1.236} = 1.618 $$

This property can be repeated infinitely, creating a sequence of increasingly smaller golden rectangles.

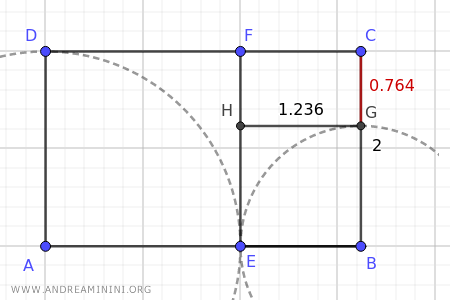
This sequence of golden rectangles allows for the creation of a "spiral."

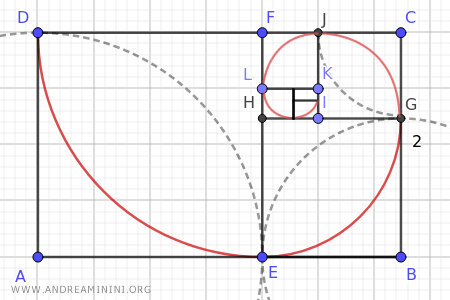
This spiral shape, achieved through the golden section, is found in nature in many shells and has inspired countless artistic and architectural works by humans.

Note. The Golden Rectangle has been extensively studied and employed in art, architecture, and design for its aesthetically pleasing properties. Many artists and architects of the past have utilized the golden ratio in their creations, believing it imparted natural proportionality and beauty.

And so on.