Golden Ratio
The Golden Ratio of a segment is that special portion of the segment that maintains a unique proportion, acting as the mean between the length of the entire segment and that of the remaining part of the segment itself.
The Golden Ratio is also known as the divine proportion, golden number, or Phi (denoted as φ).
It's a unique mathematical relationship found frequently in nature, art, architecture, and beyond.
Note. The ancient Greeks saw the Golden Ratio as the epitome of harmony in measurements. Proportions adhering to this rule are often perceived as harmonious and pleasing to the eye. Many natural phenomena closely follow the Golden Ratio. For instance, the proportions of the human body, the shape of shells, etc. For this reason, it has been frequently utilized in art and architecture as well, like in the construction of the Parthenon in Athens, Leonardo da Vinci's Vitruvian Man, and so on.
For example, consider a segment AB and divide it into two parts, AC and BC.
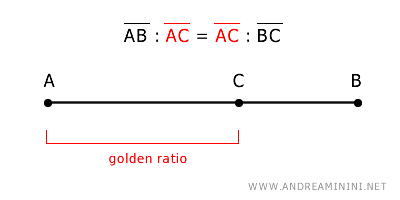
The segment AC is the Golden Ratio of the segment if it satisfies this proportion:
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{AB} $$
In this scenario, segment AC is the mean proportional between the length of the entire segment AB and the length of the remaining segment BC.
The ratio of the Golden Ratio AC to the whole segment is a constant 0.618033988749895
$$ \frac{ \overline{AC} }{ \overline{AB} } = 0.618033988749895 $$
The ratio of the entire segment AB to the section AC, on the other hand, is 1.618033988749895 and is called the Golden Number (φ)
$$ \frac{ \overline{AB} }{ \overline{AC} } = 1.618033988749895 = φ $$
Therefore, to find the length of the Golden Ratio in a segment, simply multiply the length of the entire segment AB by a constant, which for simplicity's sake is approximated to 0.618
$$ \overline{AC} = 0.618 \cdot \overline{AB} $$
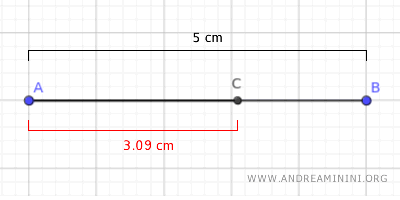
For instance, if a segment AB is 5 cm long.
The length of the Golden Ratio AC is 0.618·5 cm = 3.09 cm
$$ \overline{AC} = 0.618 \cdot 5 \ cm = 3.09 \ cm $$
How is the number 0.618 derived? To derive it algebraically, consider a unit length segment AB=1 and the length of the Golden Ratio as an unknown x. $$ 1 : x = x : (1-x) $$ Apply the fundamental property of proportions $$ x \cdot x= 1 \cdot (1-x) $$ $$ x^2 = 1-x $$ $$ x^2 + x -1 = 0 $$ Then solve the quadratic equation. $$ x = \frac{-1 \pm \sqrt{1^2-4 \cdot 1 \cdot -1}}{2} $$ $$ x = \frac{-1 \pm \sqrt{5}}{2} = \begin{cases} \frac{-1 - \sqrt{5}}{2} = \ not \ acceptable \\ \\ \frac{-1 + \sqrt{5}}{2} = 0.618033 \end{cases} $$
How to find the Golden Ratio in a segment
Consider a segment AB.

Find its midpoint M and draw a perpendicular segment from the end B.
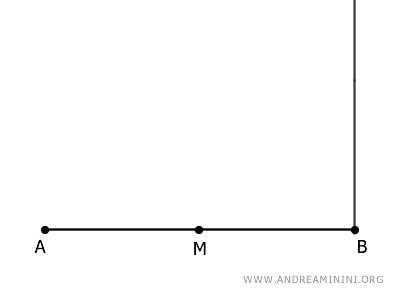
With the compass centered on point B and opened to BM, draw an arc that intersects the perpendicular segment at point C.
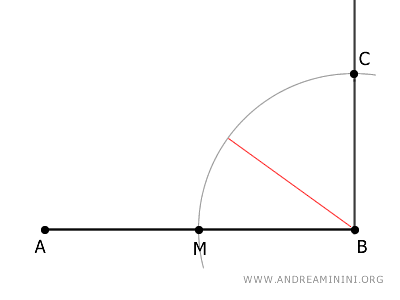
Draw the segment AC.
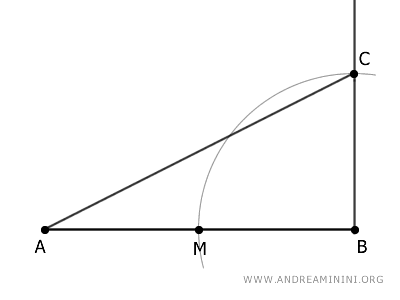
Then, with the compass centered on point C and opened to CB, draw another arc that intersects the segment AC at point D.
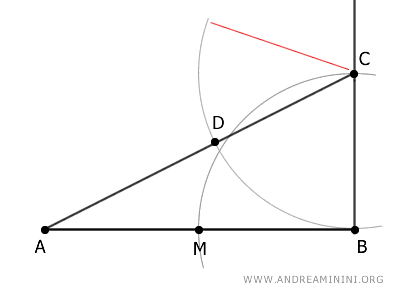
Next, center the compass on point A and with an opening AD draw a third arc that intersects the segment AB at point E.
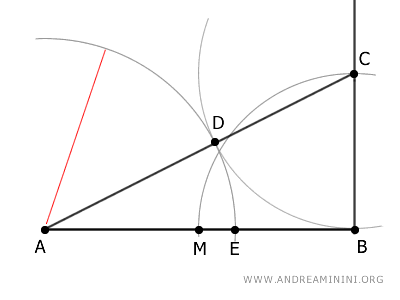
The segment AE is the Golden Ratio of segment AB.
The Proof
To demonstrate the golden ratio, let's consider the design used to construct the golden segment AE.
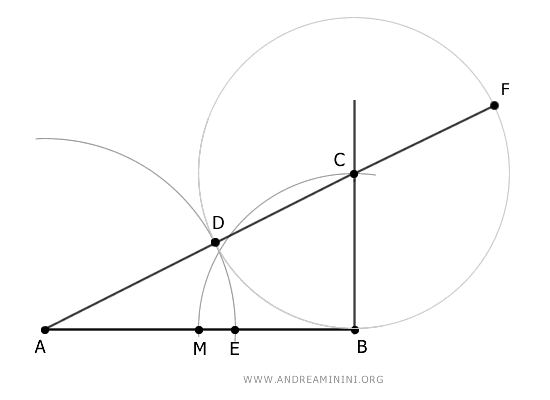
The segment AB is the tangent of the circle with center C, while the segment AF is the secant.
According to the secant-tangent theorem, these segments share a proportional relationship.
$$ \overline{AF} : \overline{AB} = \overline{AB} : \overline{AD} $$
I apply the property of proportion decomposition.
$$ ( \overline{AF} - \overline{AB} ) : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AD} $$
The circle has a radius OB ≅ BM, making the diameter of the circle CE≅AB congruent with segment AB.
$$ ( \overline{AF} - \overline{CE} ) : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AD} $$
Knowing that AF-CE is the segment AD
$$ \overline{AD} : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AD} $$
In turn, the segment AD≅AE is congruent with the golden section AE.
$$ \overline{AE} : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AE} $$
Therefore, AB-AD is congruent with AB-AE
$$ \overline{AE} : \overline{AB} = ( \overline{AB} - \overline{AE} ) : \overline{AE} $$
The difference AB-AE≅EB gives us the remainder of segment AB after the golden segment AE.
$$ \overline{AE} : \overline{AB} = \overline{EB} : \overline{AE} $$
Finally, I apply the property of proportion permutation.
$$ \overline{AB} : \overline{AE} = \overline{AE} : \overline{EB} $$
This demonstrates that segment AB relates to the golden section AE in the same way that the latter relates to the remainder of the segment EB.
Thus, the segment AE is the golden section of segment AB.
The Golden Rectangle
The Golden Rectangle is one where the ratio between the longer side and the shorter side equals the Golden Ratio, φ=1.618...
For instance, this rectangle qualifies as a Golden Rectangle.
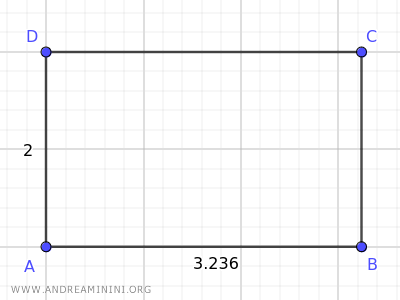
The ratio between the length of the longer side (3.235) and the shorter side (2) is roughly equal to the Golden Ratio (1.618).
$$ \frac{ \overline{AB} }{ \overline{AD} } = \frac{3.236}{2} = 1.618 $$
Removing the square formed by the shorter side from a Golden Rectangle yields another Golden Rectangle.
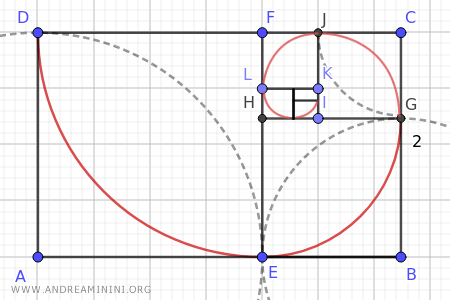
This interplay of Golden Rectangles, one nestled within another, produces a spiral curve found in many natural shell formations and is also a recurring motif in various human artworks.
And so on.
