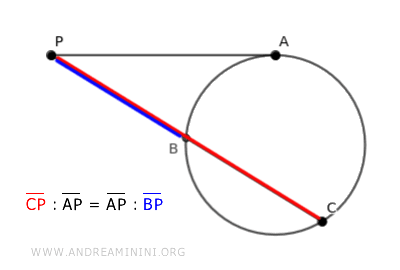
The Secant-Tangent Proportionality Theorem

Drawing a tangent and a secant from a point P outside a circle, the tangent segment is the geometric mean between the two secant segments that start from P and intersect the circle.

A Practical Example

Let's consider this scenario as an example.

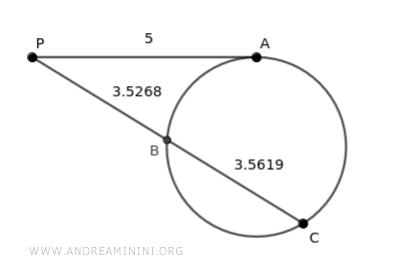
The tangent segment AP measures 5.

$$ \overline{AP} = 5 $$

The secant segment CP is equal to the sum of segments BP+BC

$$ \overline{CP} = \overline{BP} + \overline{BC} $$

$$ \overline{CP} = 3.5268+3.5619= 7.09 $$

According to the theorem, the secant segment CP relates to the tangent segment AP as AP does to BP.

$$ \overline{CP} : \overline{AP} = \overline{AP} : \overline{BP} $$

$$ 7.09 : 5 = 5 : 3.5268 $$

$$ 1.41 = 1.41 $$

This confirms the proportion, making the tangent segment the geometric mean.

Note. I've rounded the quotients to two decimal places since the segment measurements taken with Geogebra are approximate to four decimal places.

The Proof

Consider a circle and an external point P.

A tangent and a secant are drawn.

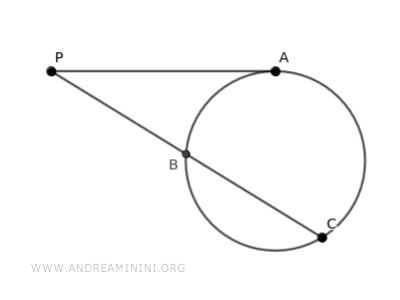
The tangent touches the circle at point A, while the secant intersects the circle at points B and C.

Two more segments, AB and AC, are drawn.

This creates two triangles, ABP and ACP.

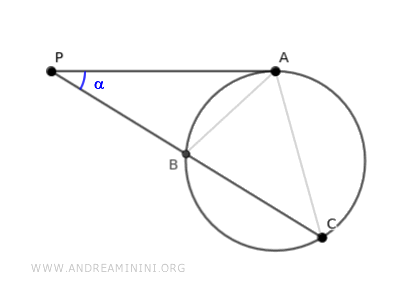
The two triangles ABP and ACP share the same angle α.

Additionally, they have congruent angles β≅γ because they are circle angles that span the same circular arc AB.

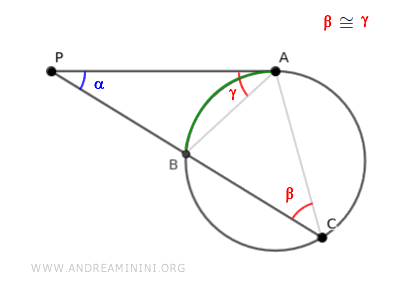
Therefore, by the first criterion of triangle similarity, triangles ABP and ACP are similar, having one coinciding angle α and one congruent angle β≅γ.

$$ ABP \approx ACP $$

Being similar triangles, their corresponding sides are proportional.

$$ \overline{AB} : \overline{AC} = \overline{BP} : \overline{AP} = \overline{AP} : \overline{CP} $$

This proves the theorem.

$$ \overline{BP} : \overline{AP} = \overline{AP} : \overline{CP} $$

The tangent segment AP is the geometric mean between the secant segments.

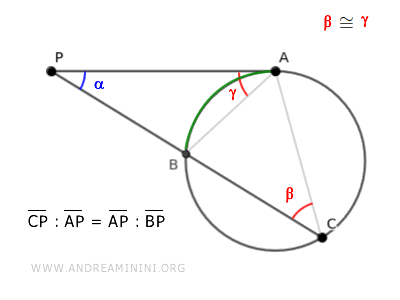
And so on.