Theorem of Proportionality of Bases and Heights in Similar Triangles
In two similar triangles, the ratio of their bases is equal to the ratio of their heights, meaning the bases and heights are proportional.
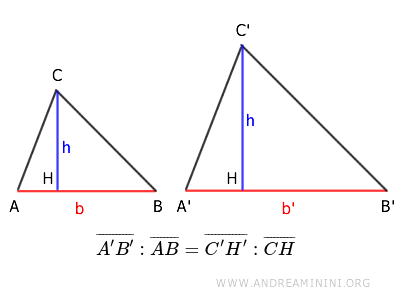
This theorem establishes the proportionality between the corresponding bases and heights of two similar triangles.
It's another significant property of similar triangles: not only the sides, but also the heights adhere to the same ratio.
A Practical Example
Let's take two similar triangles ABC and A'B'C' as an example.
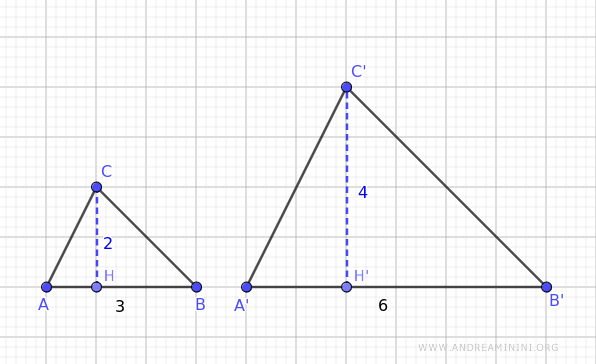
Consider the segment AB as the base of triangle ABC and the corresponding side A'B' as the base of triangle A'B'C'.
The ratio between the bases of the two similar triangles is equal to 2.
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{6}{3} = 2 $$
Now, let's calculate the ratio between the respective heights of the two triangles relative to bases AB and A'B'
$$ \frac{ \overline{C'H'} }{ \overline{CH} } = \frac{4}{2} = 2 $$
The ratio between the heights is also equal to 2, the same as the ratio of the corresponding bases.
Thus, the heights are to each other as their respective bases.
Note. This property is only valid if the two triangles are similar.
The same holds true if we take other corresponding sides of the two similar triangles as bases and their respective heights.
For example, consider sides BC and B'C' of the two triangles and their respective heights AH and A'H'.
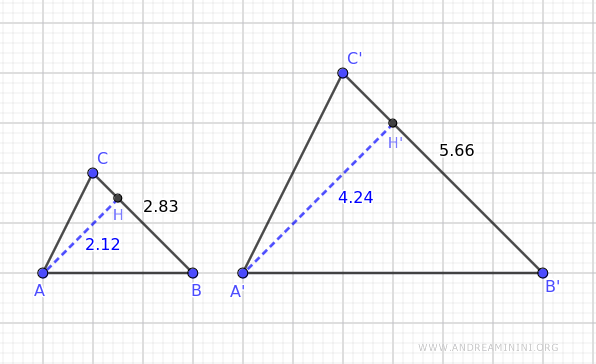
The ratio between the bases of the two similar triangles is 1.33.
$$ \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{5.66}{4.24} = 1.33 $$
The ratio between the heights of the two similar triangles is consistently 1.33.
$$ \frac{ \overline{A'H'} }{ \overline{AH} } = \frac{2.83}{2.12} = 1.33 $$
The end result is always the same. In similar triangles, the bases are to each other as their respective heights, and vice versa.
The Proof
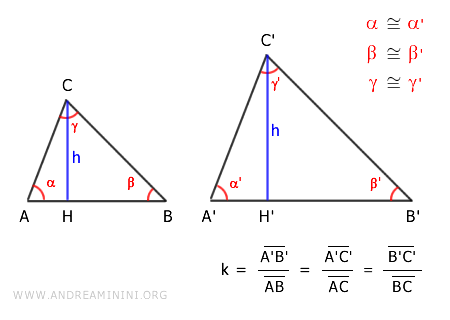
Consider two similar triangles ABC and A'B'C'.
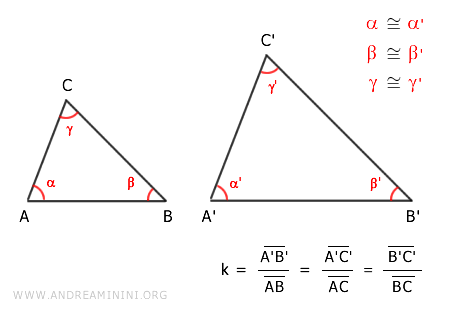
Being similar, the two triangles have congruent angles α≅α', β≅β', γ≅γ' and proportional corresponding sides
$$ \overline{A'B'} : \overline{AB} = \overline{A'C'} : \overline{AC} = \overline{B'C'} : \overline{BC} $$
In other words, there exists a common proportionality factor k among the corresponding sides of the triangles
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{A'C'} }{ \overline{AC} } = \frac{ \overline{B'C'} }{ \overline{BC} } = k $$
Consider the segment AB as the base of triangle ABC and the corresponding side A'B' as the base of triangle A'B'C'.
Therefore, the respective heights are the segments CH and C'H'.
Examining the right-angled triangles ACH and A'C'H' formed by the height in both triangles.
According to the first criterion of similarity for triangles, the right-angled triangles ACH and A'C'H' are similar, as they have proportional sides and the angle between them congruent α≅α'.
$$ ACH \approx A'C'H' $$
Being similar, the right-angled triangles ACH and A'C'H' have all sides proportional.
$$ \overline{A'C'} : \overline{AC} = \overline{C'H'} : \overline{CH} $$
Where AC and A'C' are corresponding sides of the two triangles ABC and A'B'C' while CH and C'H' are their respective heights.
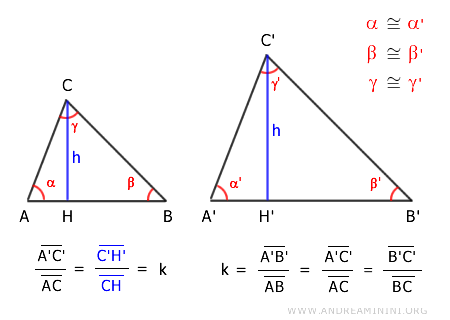
Knowing that the sides of the two triangles ABC and A'B'C' are proportional, since the triangles are similar, it follows that the heights have the same proportion as the bases
$$ \overline{A'B'} : \overline{AB} = \overline{C'H'} : \overline{CH} $$
This proves that the two similar triangles have proportional bases and heights.
And so on.
