Third Criterion for Triangle Similarity
Two triangles are similar if their corresponding sides are proportional.
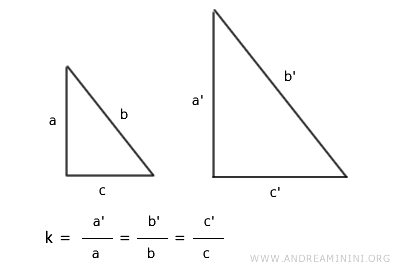
According to this criterion, when two triangles have sides that are proportionally equivalent, they form similar figures.
This method of determining triangle similarity is also known as the SSS (Side-Side-Side) criterion.
A Practical Example
Consider two triangles ABC and A'B'C' with sides proportional in the same sequence.
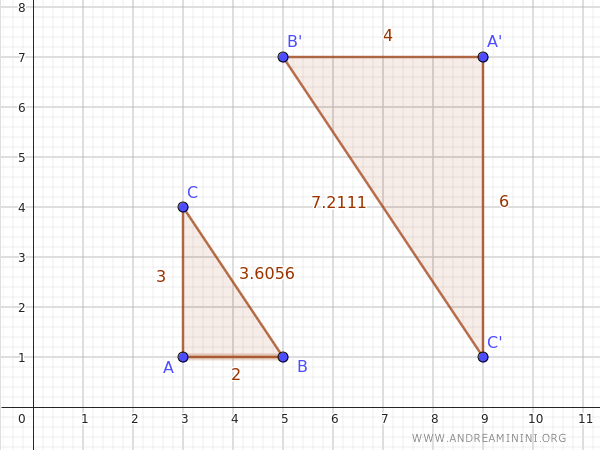
In this case, the proportionality ratio is 2.
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{4}{2} = 2 $$
$$ \frac{ \overline{A'C'} }{ \overline{AC} } = \frac{6}{3} = 2 $$
$$ \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{7.2}{3.6} = 2 $$
By the third criterion for triangle similarity, triangles ABC and A'B'C' are similar triangles.
$$ ABC \approx A'B'C' $$
Indeed, the two triangles are similar because they have congruent angles in the same sequence.
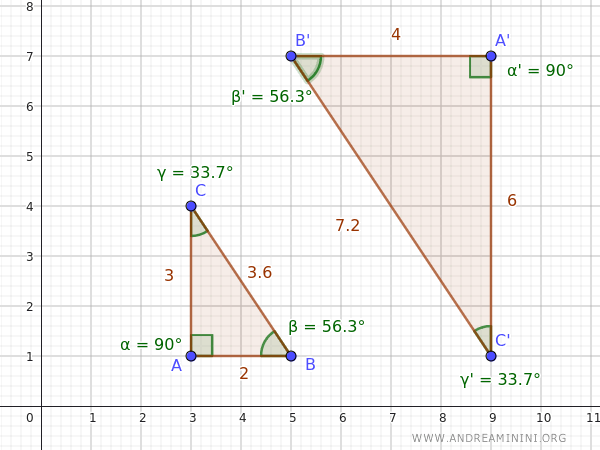
Thus, they share the same shape but differ in size.
Proof
Consider two triangles ABC and A'B'C'
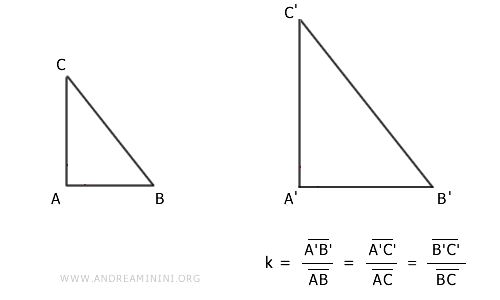
By hypothesis, the sides of the two triangles are proportional in the same sequence
$$ \overline{A'B'}:\overline{AB} = \overline{B'C'}:\overline{BC} = \overline{A'C'}:\overline{AC} $$
I express the proportion in the form of an equality between fractions.
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = k $$
The proportionality ratio is k.
I aim to demonstrate the similarity between the two triangles.
$$ ABC \approx A'B'C' $$
To do this, I examine two cases: one where sides AC and A'C' are congruent and the opposite case where they are not.
1] The sides AB and A'B' are congruent
In this scenario, sides AB and A'B' are congruent
$$ \overline{A'B'} \cong \overline{AB} $$
This means they have the same length. Hence, the proportionality ratio is k=1.
$$ k = \frac{ \overline{A'B'} }{ \overline{AB} } = 1 $$
This implies that the other two sides also share the same proportionality ratio
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \ overline{AC} } = k=1 $$
Therefore, all sides of the triangles are congruent in the same sequence.
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
$$ \overline{AC} \cong \overline{A'C'} $$
By the third criterion of triangle congruence, triangles ABC and A'B'C' are congruent because all corresponding sides are congruent.
$$ ABC \cong A'B'C' $$
Congruent figures are also similar, with a similarity ratio of k=1, hence triangles ABC and A'B'C' are similar.
2] The sides AB and A'B' are not congruent
In this case, sides AB and A'B' are not congruent, indicating different lengths.
This means the proportionality ratio between the two segments is not 1.
$$ k = \frac{ \overline{A'C'} }{ \overline{AC} } \ne 1 $$
Therefore, the other corresponding sides of the two triangles are also not congruent
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = k \ne 1 $$
Using the same ratio k, I construct a homothety on triangle ABC with point A as the center of homothety.
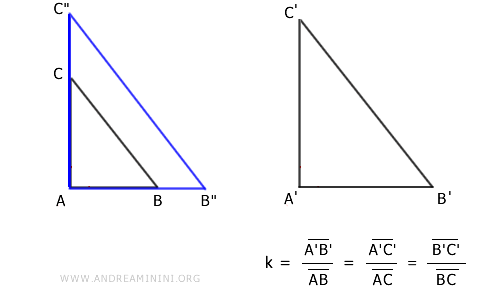
This results in triangle A"B"C", a homothetic transformation of triangle ABC.
Triangles A"B"C" and ABC are similar because any homothetic transformation of a figure produces a similar figure.
$$ A"B"C" \approx ABC $$
The chosen homothety ratio k matches the proportionality ratio between the corresponding sides of triangles ABC and A'B'C'.
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = k $$
Consequently, the homothetic triangle A"B"C" has corresponding sides of the same length as triangle A'B'C'.
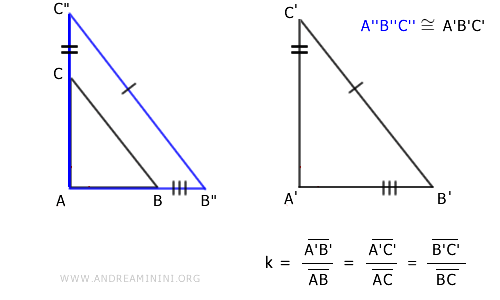
Therefore, by the third criterion of triangle congruence, triangles A"B"C" and A'B'C' are congruent.
$$ A'B'C' \cong A''B''C'' $$
Being congruent, the two triangles are also similar with a similarity ratio k=1.
$$ A'B'C' \approx A''B''C'' $$
Knowing that triangle A'B'C' in turn is similar to triangle ABC, as it is a homothetic transformation of the latter, it follows that triangles A'B'C' and ABC are also similar.
$$ A'B'C' \approx A''B''C'' \approx ABC $$
Thus, in this case too, triangles A'B'C' and ABC are similar.
3) Conclusion
In both scenarios, whether sides AB and A'B' are congruent or not, triangles ABC and A'B'C' are similar figures.
This demonstrates the third criterion for triangle similarity.
And so on.
