Second Criterion for Triangle Similarity
Two triangles are deemed similar if they share two corresponding sides that are proportional and an angle between those sides that is congruent.
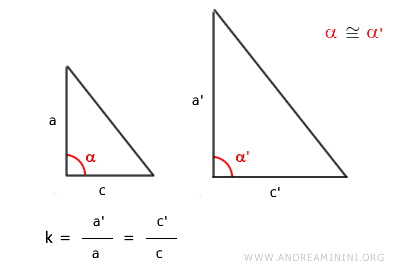
This means that if two triangles have sides in the same proportion and the angle adjacent to those sides matches, they are considered similar figures.
This principle is commonly referred to as the SAS (Side Angle Side) similarity criterion.
An Illustrative Example
Consider two triangles, ABC and A'B'C', for instance.
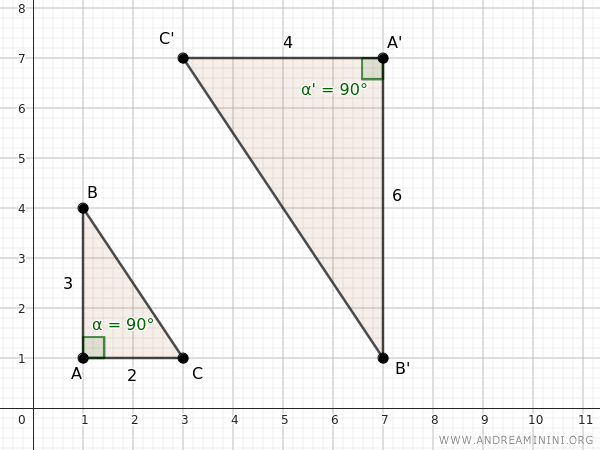
These triangles have proportional sides AB to A'B' and AC to A'C'
$$ \overline{AB} : \overline{A'B'} = \overline{AC}:\overline{A'C'} $$
expressed as a fraction, this becomes
$$ \frac{ \overline{AB} }{ \overline{A'B'}} = \frac{ \overline{AC} }{ \overline{A'C'}} $$
Given that AB=3, AC=2, A'B'=6, and A'C'=4,
$$ \frac{ 3 }{ 6} = \frac{ 2 }{ 4} $$
$$ \frac{ 1 }{ 2} = \frac{ 1 }{ 2} $$
Additionally, they share a congruent angle α≅α', as it is a right angle in both instances.
$$ \alpha \cong \alpha' $$
By applying the second criterion of similarity, it's determined that triangles ABC and A'B'C' are similar triangles.
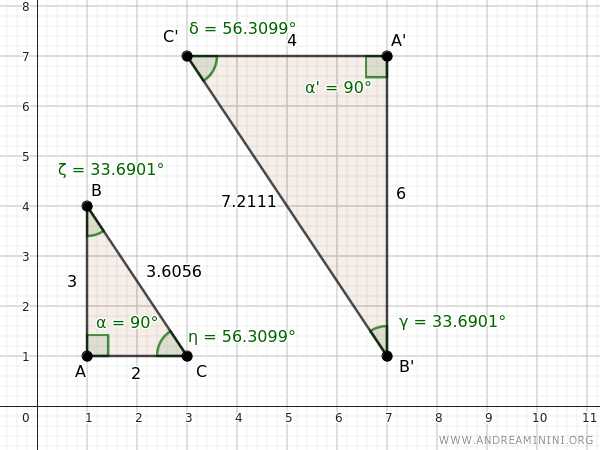
Indeed, their similarity is confirmed by their congruently ordered angles and proportional corresponding sides.
Proof
Let’s delve into two triangles, ABC and A'B'C', as our subjects.
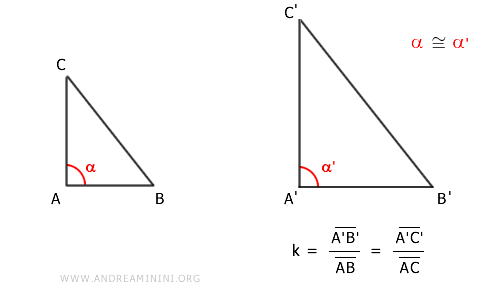
Initially, it’s observed that sides AB and AC of triangle ABC correspond proportionally with sides A'B' and A'C' of triangle A'B'C'.
$$ \overline{A'B'} : \overline{AB} = \overline{A'C'} : \overline{AC} $$
which simplifies to
$$ \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{A'C'}}{\overline{AC}} = k $$
Moreover, the angle α between sides AB and AC aligns with angle α' between sides A'B' and A'C',
$$ \alpha \cong \alpha' $$
My task is to prove the similarity of the two triangles
$$ ABC \approx A'B'C' $$
For this purpose, let's examine whether sides AB and A'B' are either congruent or not.
1) When Sides AB and A'B' Are Congruent
If sides AB and A'B' are congruent, then it follows from our initial hypothesis that sides AC and A'C' are also congruent.
$$ \overline{AB} : \overline{A'B'} = \overline{AC} : \overline{A'C'} $$
Note: The congruence of AB and A'B' suggests that the ratio AB/A'B' equals one. $$ 1 = \overline{AC} : \overline{A'C'} $$ Multiplying both sides of this equation by A'C' results in $$ \overline{A'C'} = \overline{AC} $$ Hence, sides AC and A'C' are of equal length, or congruent AC≅A'C'
Having established that sides AB≅A'B' and AC≅A'C' are congruent, by the first criterion of triangle congruence, it follows that triangles ABC and A'B'C' are congruent as well.
$$ ABC \cong A'B'C' $$
As congruent figures are inherently similar with a similarity ratio of 1, the two triangles are indeed similar.
$$ ABC \approx A'B'C' $$
2) When Sides AB and A'B' Are Not Congruent
If sides AB and A'B' are not congruent, I calculate their ratio.
$$ k = \frac{\overline{A'B'}}{AB} $$
A homothety centered at A with ratio k yields a new triangle AB"C".
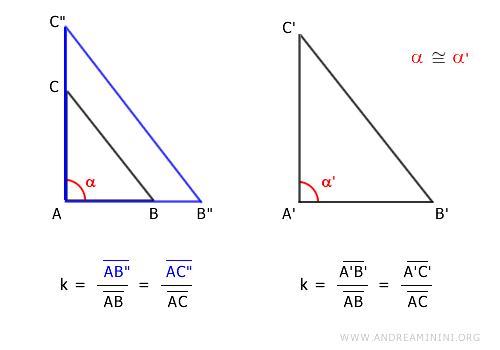
Note: Point A was deliberately chosen as the homothety center to streamline the proof, preserving angle α as a constant feature of the transformation. This decision aids in the clarity of the subsequent proof steps. Choosing another point would have led to the same conclusion but would have extended the explanation.
In this new triangle, point A remains a static point throughout the transformation.
The construction ensures that sides AB to AB" and AC to AC" are proportional by a factor of k.
$$ \frac{\overline{AB"}}{\overline{AB}} = \frac{\overline{AC"}}{\overline{AC}} = k $$
Given the initial proportion
$$ \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{A'C'}}{\overline{AC}} = k $$
I conclude that segments A'B'≅AB" and A'C'=AC" are congruent.
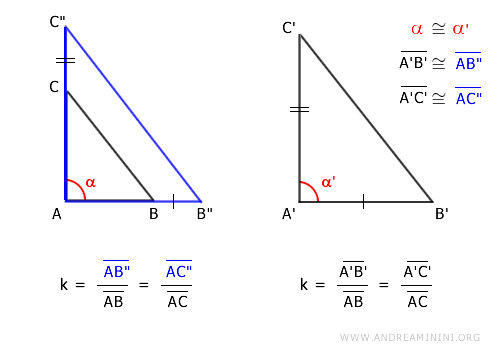
With the initial hypothesis also confirming angle α≅α' as congruent,
The triangles A'B'C'≅AB"C" are congruent by the first criterion of triangle congruence, having two congruent sides A'B'≅AB" and A'C'=AC" and the congruent angle α≅α' situated between them.
$$ A'B'C' \cong AB"C" $$
Given that the triangle AB"C" is similar to ABC as each homothetic transformation also constitutes a similarity,
$$ AB"C" \approx ABC $$
Explanation: Seeing similarity as a combination of homothety and isometry, the homothetic transformation of a figure is confirmed to be similar to the original figure. Consequently, triangle AB"C" mirrors the similarity to triangle ABC.$$ AB"C" \approx ABC $$
Since A'B'C'≅AB"C", it follows that triangle A'B'C' mirrors the similarity to triangle ABC.
$$ A'B'C' \approx ABC $$
3) Final Thoughts
Regardless of whether sides AB and A'B' are congruent or not, it's demonstrated that triangles ABC and A'B'C' adhere to the principles of similarity.
This establishes the validity of the second criterion for triangle similarity.
And so the explanation unfolds.
