Criteria for Triangle Similarity
The criteria for triangle similarity lay out the essential conditions under which two triangles are deemed similar.
This guidance is invaluable, enabling the assessment of similarity between two triangles without the need to scrutinize every aspect.
There are three main criteria for establishing similarity.
The Angle-Angle-Angle (AAA) Criterion
Two triangles are similar if they have two congruent corresponding angles.
When triangles share two congruent internal angles in a matching sequence, it guarantees the congruence of the third internal angle as well.
Thus, these triangles maintain identical shapes within the plane, though their sizes may differ.
This is also referred to as the AAA Similarity Criterion.
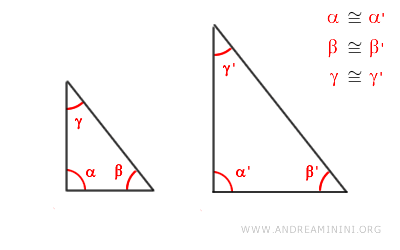
For example, if two triangles have two congruent corresponding angles α≅α' and β≅β',
$$ \alpha \cong \alpha ' $$
$$ \beta \cong \beta ' $$
they fulfill the similarity criterion and are thus similar.
Note: It's enough to confirm that any two corresponding angles are congruent in a triangle, given the sum of a triangle's internal angles always equals 180°. Hence, if two triangles share two congruent angles α and β, the third angle automatically matches as the remainder to 180°, i.e., γ≅180°-α-β. This principle holds for any pair of corresponding internal angles.
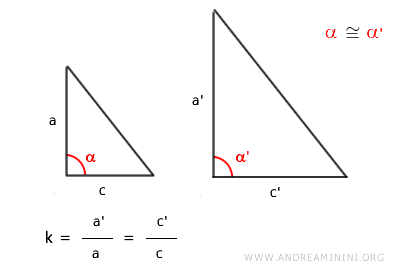
The Side-Angle-Side (SAS) Similarity Criterion
Two triangles are similar if they have two corresponding sides in proportion and the included angle is congruent.
When two triangles exhibit proportionally equivalent sides, following the same ratio k, and the angle between those sides is congruent, they are recognized as similar.
This criterion is also known as the SAS Similarity Criterion.
The Side-Side-Side (SSS) Similarity Criterion
Two triangles are similar if all their corresponding sides are proportionate.
If every side of two triangles is proportionally equivalent, adhering to the same ratio k, then they are affirmed to be similar.
This is also termed the SSS Similarity Criterion.
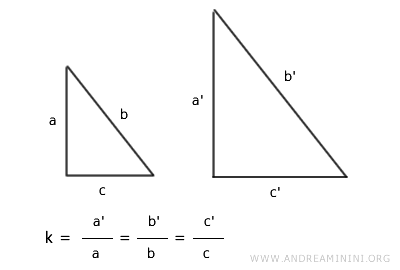
And that's the gist of it.
