Golden Number
The Golden Number is approximately the irrational number $$\phi = 1.6180339887...$$
It is often represented by the Greek letter φ (phi).
This irrational number has captivated mathematicians, artists, and architects for centuries due to its properties and its supposed connection to aesthetics and natural harmony.
Note. Historically, it was believed that proportions defined by the Golden Ratio are particularly pleasing to the eye. This led to its application across various disciplines, from painting and sculpture to architecture. For instance, the Parthenon in Athens embodies the proportions of the Golden Ratio, as do many Renaissance artworks. The ratio is also said to appear in natural phenomena, such as the spiral shape of the Nautilus shell, although some of its purported occurrences in nature are likely overstated.
How Is It Derived?
The Golden Ratio is derived by considering two segments, \(a\) and \(b\), with \(a > b\), such that the ratio of the sum of the two segments (\(a + b\)) to the longer segment (\(a\)) is equal to the ratio of the longer segment (\(a\)) to the shorter (\(b\)). Mathematically, this is expressed as:
$$ \frac{a + b}{a} = \frac{a}{b} = \phi $$
This relationship yields a value of:
$$ \phi = \frac{1 + \sqrt{5}}{2} \approx 1.6180339887... $$
The Proof
Let's explore why the ratio between the longer segment "a" and the shorter "b" equals 1.618...
Starting with the relationship between the two segments as our base assumption:
$$ \frac{a + b}{a} = \frac{a}{b} = \phi $$
The ratio of the sum of the two segments (\(a + b\)) to the larger segment \(a\) is equal to \(\phi\).
$$ \frac{a + b}{a} = \phi $$
The ratio of the larger segment \(a\) to the smaller segment \(b\) is also equal to \(\phi\).
$$ \phi = \frac{a}{b} $$
From this, we infer that segment "b" equals the ratio \( \frac{a}{ \phi } \)
$$ b = \frac{a}{ \phi } $$
Focusing on the first part of the relationship:
$$ \frac{a + b}{a} = \phi $$
Knowing that \( b = \frac{a}{ \phi } \).
$$ \frac{a + \frac{a}{\phi}}{a} = \phi $$
Simplifying the equation by dividing both sides by \(a\):
$$ 1 + \frac{1}{\phi} = \phi $$
This equation can be rewritten as:
$$ \frac{1}{\phi} = \phi - 1 $$
Multiplying both sides by \(\phi\) gives us a quadratic equation in \(\phi\):
$$ 1 = \phi^2 - \phi $$
Rearranging terms:
$$ \phi^2 - \phi - 1 = 0 $$
This is a quadratic equation that can be solved using the quadratic formula:
$$ \phi = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Where \(a = 1\), \(b = -1\), and \(c = -1\). Substituting these values, we get:
$$ \phi = \frac{-(-1) \pm \sqrt{(-1)^2 - 4(1)(-1)}}{2(1)} = \frac{1 \pm \sqrt{1 + 4}}{2} = \frac{1 \pm \sqrt{5}}{2} $$
Since \(\phi\) is a positive ratio, we use the \(+\) sign, resulting in:
$$ \phi = \frac{1 + \sqrt{5}}{2} \approx 1.6180339887... $$
This explanation shows how the relationship directly leads to the value of the Golden Ratio (1.618...) through straightforward algebraic steps and the use of the quadratic formula.
A Practical Example
The Golden Ratio is closely linked to the Fibonacci sequence, a series where each number is the sum of the two preceding ones (0, 1, 1, 2, 3, 5, 8, 13, 21, ...).
$$ \sigma = 0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , ... $$
The ratio between successive numbers in the Fibonacci sequence approaches the Golden Ratio as we move to higher numbers.
$$ \frac{1}{1} \ , \ \frac{2}{1} \ , \ \frac{3}{2} \ , \ \frac{5}{3} \ , \ \frac{8}{5} \ , \ \frac{13}{8} \ , \ \frac{21}{13} \ , \ \ \frac{34}{21} \ , \ ... $$
Calculating these quotients reveals a trend toward the Golden Ratio (1.618...).
$$ 1 , 2 , 1.5 , 1.666 , 1.6 , 1.625 , 1.615 , 1.619 , ... $$
Observations
Some additional notes on the Golden Ratio:
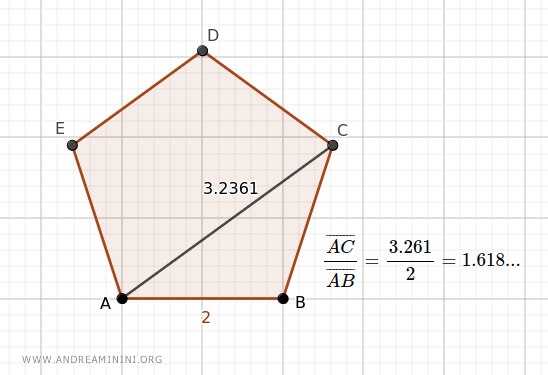
- The ratio between the diagonal and the side of a regular pentagon equals the Golden Ratio
For example, the ratio between the diagonal AC of a regular pentagon and its side AB is approximately 1.618...
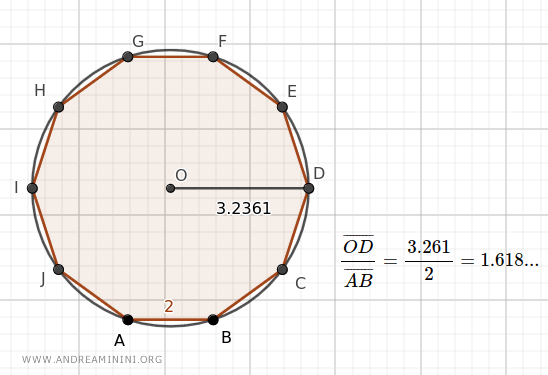
- The ratio between the radius of a circle and the side of an inscribed regular decagon equals the Golden Ratio
In this regular decagon, the ratio between the radius of the circle (3.2361) and the side of the decagon (2) equals the Golden Ratio.