The Side of a Regular Decagon Is the Golden Ratio of Its Radius
The side of a regular decagon is the golden section of the radius of the circumscribed circle $$ r : l = l : (r-l) $$
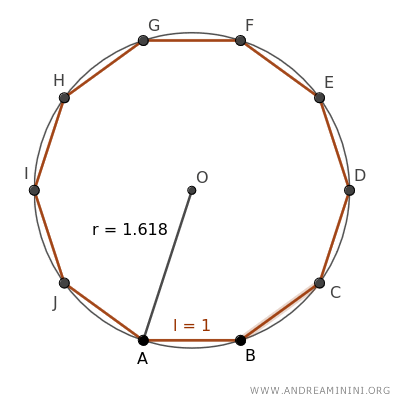
In other words, in a regular decagon, the ratio of the circumscribed circle's radius to the decagon's side is equal to the golden ratio, 1.618...
A Practical Example
Let's consider a regular decagon with each side measuring 1 unit in length.
The radius of the circumscribed circle around the decagon equals 1.618... or the golden ratio.

The segment AK is congruent to side AB, hence it measures 1 unit in length.
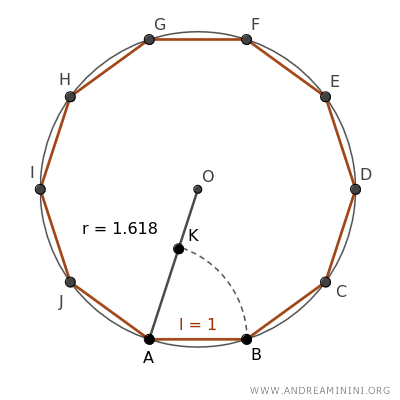
Next, I check if the golden ratio proportion holds true.
$$ \overline{AB} : \overline{AK} = \overline{AK} : \overline{OK} $$
Given that OK=1 and AB=1.618...
$$ 1.618 : 1 = 1 : \overline{OK} $$
The segment OK is congruent with the difference between the segments OA-OK, which is 1.618-1=0.618
$$ 1.618 : 1 = 1 : 0.618 $$
Performing the two divisions, I get the same result
$$ 1.618 = 1.618 $$
The proportion is satisfied, therefore the side (AB) of the decagon is the golden section of the radius (OA) of the circumscribed circle.
Demonstration
I construct a regular decagon, a polygon with 10 congruent sides.
All regular polygons can be circumscribed.
Thus, I find the center of the decagon in order to draw the circumscribed circle around the polygon, with O as its center and a radius of length r.
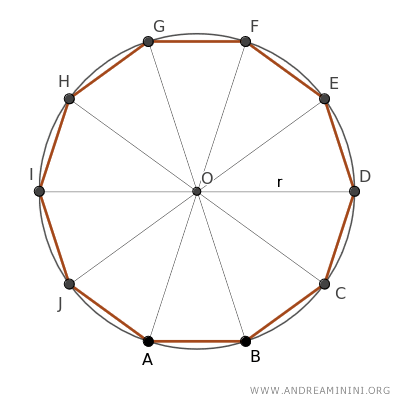
This divides the decagon into 10 congruent triangles, because according to the third criterion of triangle congruence, they all have three congruent sides.
$$ ABO \cong BCO \cong CDO \cong ... $$
All the triangles have a vertex angle at O of 36° because the full angle (360°) was divided into 10 equal parts.
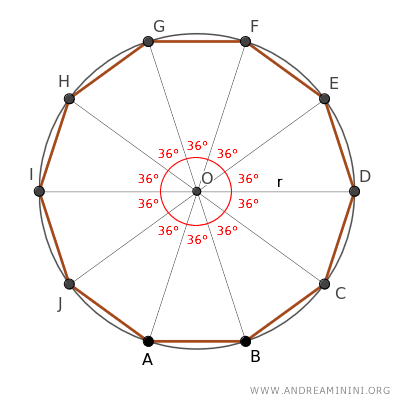
I continue the analysis on triangle ABO, as the properties demonstrated on any one of these triangles apply to all the others due to their congruence.
The triangle ABO is an isosceles triangle because it has two congruent oblique sides AO≅AB to the radius of the circle.
Being an isosceles triangle, it has two base angles α≅β that are congruent.
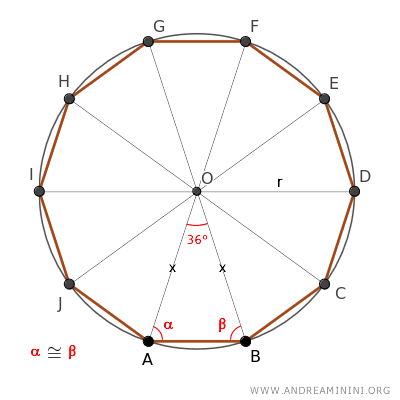
The sum of the interior angles of any triangle always equals 360°
$$ \alpha + \beta + 36° = 180° $$
Therefore, I deduce that the sum of angles α+β equals the difference between 360° and 36°
$$ \alpha + \beta = 180° - 36° $$
$$ \alpha + \beta = 144° $$
Knowing that α≅β are congruent and their sum is α+β=144°, I deduce that each angle measures half of 144°, hence α=72° and β=72°.
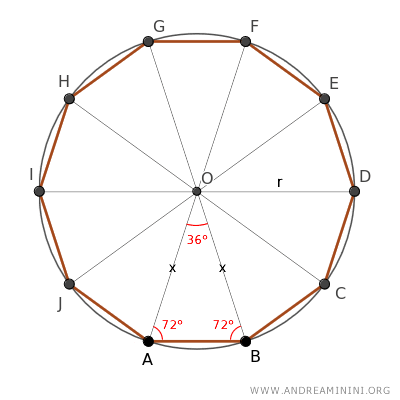
Next, I draw the bisector of one of the base-adjacent angles of triangle ABO, which divides the angle (72°) into two congruent angles of 36° each.
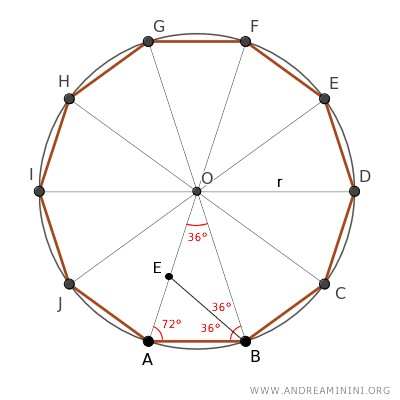
The triangle BOE is another isosceles triangle because it has two congruent angles (36°) adjacent to the base OB.
Therefore, the oblique sides OE≅BO are congruent.
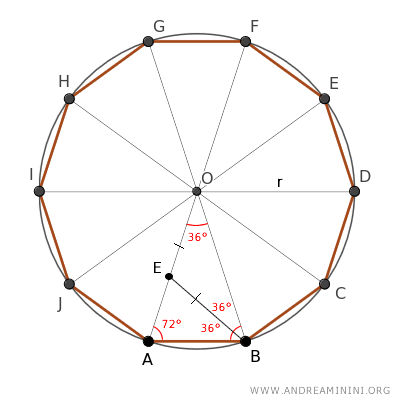
Examining the other triangle ABE, I realize I already know two of its angles, so I can deduce the measure of the third angle by difference, which is 180°-72°-36°=72°.
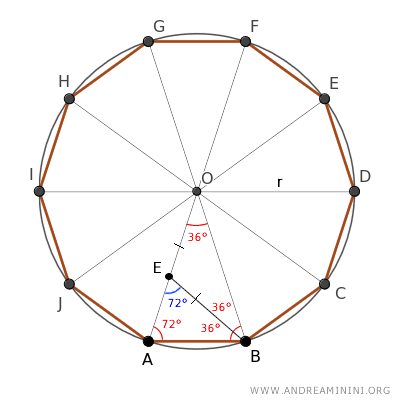
Therefore, the triangle ABE is also an isosceles triangle because it has two congruent angles (72°) adjacent to a side.
As a result, being isosceles, it has congruent oblique sides AB≅BE.
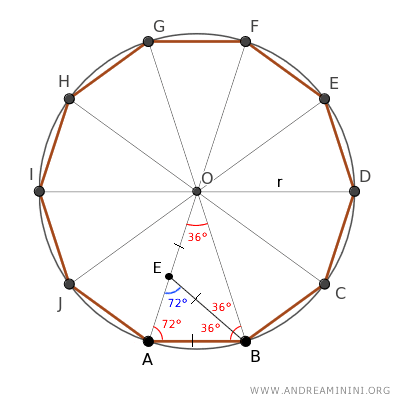
Consequently, knowing AB≅EB and EB≅OE, I deduce that the segments AB≅OE are congruent as well.
The triangles ABO and ABE are similar, because according to the first criterion of triangle similarity, they have two congruent angles (36°, 72°).
$$ ABO \approx ABE $$
Therefore, being similar, the triangles ABO and ABE have proportional corresponding sides.
$$ \overline{OB} : \overline{AB} = \overline{AB} : \overline{EA} $$
Given that OB is the radius (r) of the circle and AB is the side (l) of the polygon.
$$ r : l = l : \overline{EA} $$
The EA segment equals the difference between OA and OE.
$$ \overline{EA} = \overline{OA} - \overline{OE} $$
Where OA is the radius, while OE ≅ AB is congruent with the side (l) AB of the decagon.
$$ \overline{EA} = r - l $$
Thus, the EA segment is the difference between the radius and the side of the decagon.
$$ r : l = l : \overline{EA} $$
$$ r : l = l : r - l $$
This demonstrates that in a decagon, the radius (r) of the circumscribed circle is to the side (l) of the decagon, as the side (l) is to the difference between the radius and the side.
Consequently, the segment (l) is the mean proportional between the segment (r) and the difference (r-l), that is, it is the golden section of the segment r.
And so on.
