Regular Polygons

Regular polygons are flat geometric shapes where all sides and angles are equal.

In simpler terms, a regular polygon is both equilateral and equiangular, meaning all its sides are the same length, and all its angles are the same size.

Examples. Some common examples of regular polygons include the equilateral triangle, the simplest regular polygon with three equal sides and 60° angles, and the square, which has four equal sides and four right angles.

In contrast, a rhombus is not a regular polygon because, while all its sides are congruent, its angles are not. Similarly, a rectangle is not a regular polygon because, although all its angles are right angles, its sides are of different lengths.

Measuring Angles

In a regular polygon with n sides, known as an n-gon, each interior angle has the same measure (α), which can be calculated using the following formula:

$$ \alpha = (n−2) \cdot \frac{180°}{n} $$

For example, in a regular hexagon (n=6 sides), each interior angle measures 120°.

$$ \alpha = (6−2) \cdot \frac{180°}{6} = 4 \cdot 30° = 120° $$

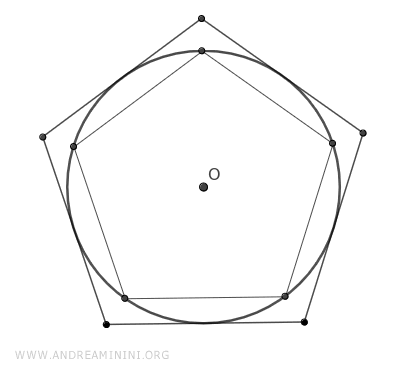
Inscribed and Circumscribed Circles of Regular Polygons

A regular polygon can be inscribed in an outer circle and circumscribed around an inner circle, with both circles sharing the same center (O), known as the center of the polygon.

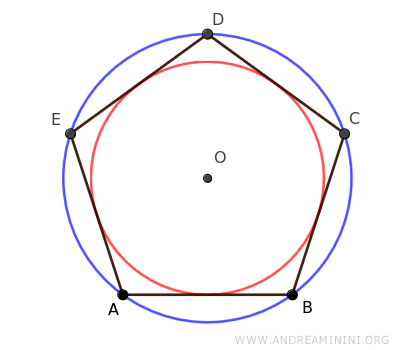
In other words, all regular polygons can be inscribed in a circle, meaning all their vertices touch the circle.

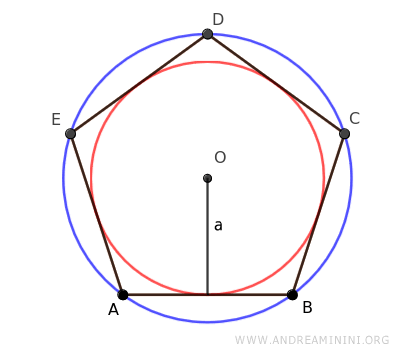
The radius of the circumscribed circle (blue) is also the distance from the center of the polygon to each of its vertices, known as the radius of the regular polygon.

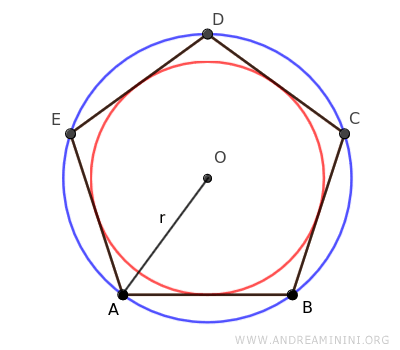
Regular polygons can also be circumscribed around an inner circle (red), where all sides are tangent to the circle.

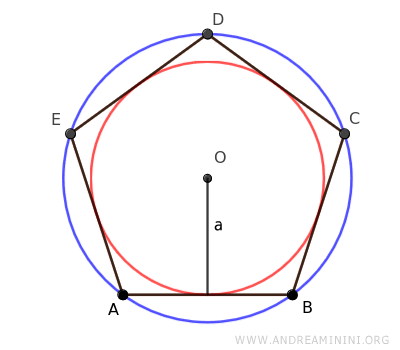
The radius of the inscribed circle is called the apothem (a).

Proof

Let's consider a regular polygon as our starting point. For example, a pentagon.

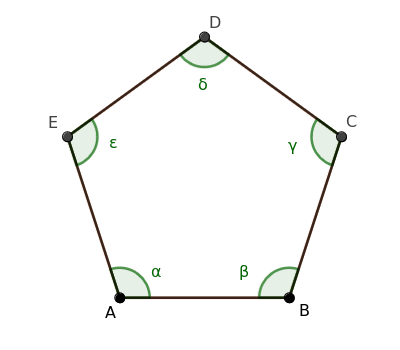
Since it's a regular polygon, it is both equilateral and equiangular.

$$ \overline{AB} \cong \overline{BC} \cong \overline{CD} \cong \overline{DE} \cong \overline{EA} $$

$$ \alpha \cong \beta \cong \gamma \cong \delta \cong \epsilon $$

We need to prove that it can be inscribed in an outer circle and circumscribed around an inner circle. Additionally, we need to prove that both circles share the same center.

To do this, we draw the bisectors of angles α and β, dividing them into two congruent halves, α'≅α'' and β'≅β''.

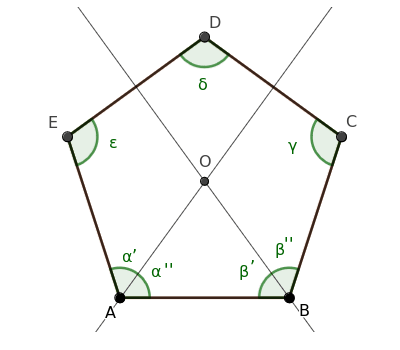
Let O be the point where the two bisectors intersect.

Since α≅β are congruent angles (by our initial hypothesis), their halves are also congruent: α'≅α''≅β'≅β''.

$$ \alpha' = \alpha'' \cong \beta' = \beta'' $$

As a result, triangle ABO is an isosceles triangle because it has two congruent angles (α''≅β') at the base.

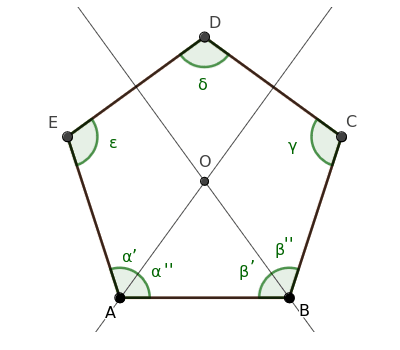
An isosceles triangle has two congruent sides, so segments OA≅OB are congruent.

$$ \overline{OA} \cong \overline{OB} $$

Next, we draw segment OC between point O and vertex C of the regular polygon.

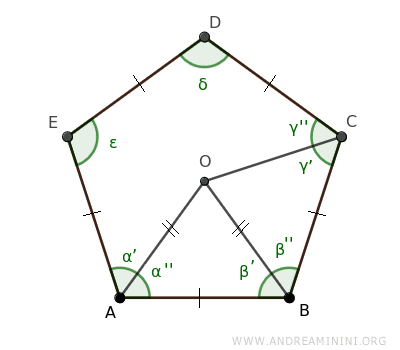
Triangles ABO and BCO are congruent by the first triangle congruence theorem because they share a side (BO), have a congruent side (AB≅BC), and have congruent angles by construction (β'≅β'').

Since the triangles ABO and BCO are congruent, all their corresponding sides and angles are also congruent.

This means that sides OC≅OB and angles α''≅γ' are congruent.

$$ \overline{OC} \cong \overline{OB} $$

$$ \alpha'' \cong \gamma' $$

Knowing that α''≅γ' and α''≅α', by the transitive property, we can conclude that α'≅α''≅γ'.

$$ \alpha' \cong \alpha'' \cong \gamma' $$

Since α≅γ by the initial hypothesis, and α'+α''=α/2 by the construction of the bisector, we can deduce that γ'+γ''=γ/2.

Therefore, γ'≅γ'', and segment OC is the bisector of angle γ.

$$ \gamma' \cong \gamma'' $$

We can repeat this process for the other vertices of the regular polygon (D, E), finding that the triangles OCD≅ODE≅OEA are also congruent isosceles triangles.

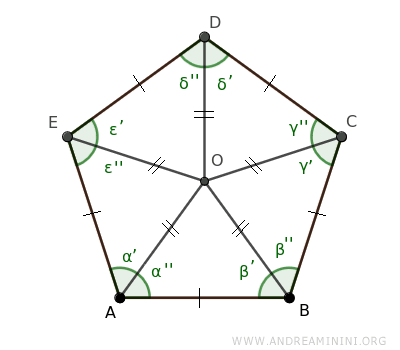
As a result, the segments OA, OB, OC, OD, and OE are congruent.

$$ \overline{OA} \cong \overline{OB} \cong \overline{OC} \cong \overline{OD} \cong \overline{OE} $$

This means that point O is equidistant from vertices A, B, C, D, and E of the regular polygon.

Since O is equidistant from the vertices of the polygon, we can draw a circle that passes through all the vertices of the polygon.

This is how we find the circumscribed circle of the polygon.

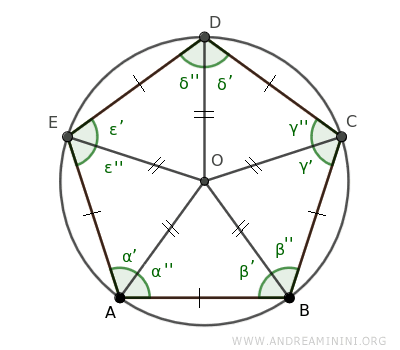
Point O is also the intersection point of all the bisectors of the isosceles triangles OAB, OBC, OCD, ODE, and OEA.

Since the points on a bisector are equidistant from the sides of the angle, we can conclude that point O is equidistant from all the sides of triangles OAB, OBC, OCD, ODE, and OEA.

Thus, if we draw a circle centered at O with a radius equal to the distance from O to any side of the triangles, the circle will touch and be tangent to all the sides of the regular polygon.

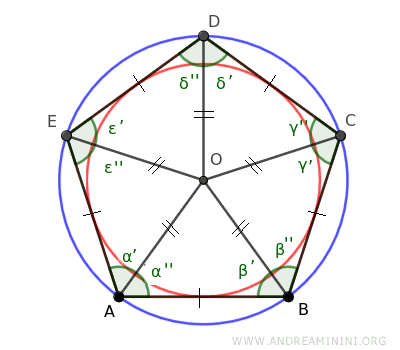
This is how we find the inner circle that the polygon circumscribes.

Moreover, the inscribed and circumscribed circles share the same center O.

This completes the proof of the initial theorem.

Apothem

The apothem is the shortest distance from the center of the polygon to any of its sides and is the radius of the circle inscribed within a regular polygon.

This value is particularly useful for calculating the area of a regular polygon.

The area (A) of a regular polygon can be found by multiplying the perimeter (P) by the apothem (a) and dividing by two:

$$ A = \frac{P \cdot a}{2} $$

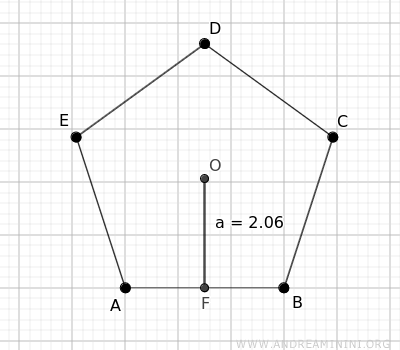
Example. A pentagon has sides of length 3 and an apothem of a=2.06. First, calculate the perimeter of the pentagon: $$ P = 3 \cdot 5 = 15 $$ Then, using the apothem a=2.06, calculate the area of the pentagon. $$ A = \frac{P \cdot a}{2} = \frac{15 \cdot 2.06}{2} = 15.45 $$ The area of the pentagon is A=15.45.

Area of a Regular Polygon

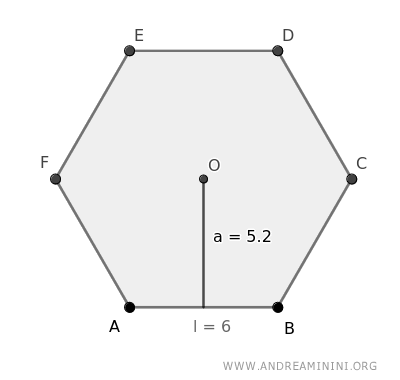
The area of a regular polygon is equal to the product of the semiperimeter (p) and the apothem (a) of the regular polygon: $$ A=p \cdot a $$

Here, the apothem is the segment that measures the distance from each side to the center of the polygon, while the semiperimeter is half the perimeter, 2p=P, so p=P/2.

This occurs because a regular polygon can be divided into multiple triangles.

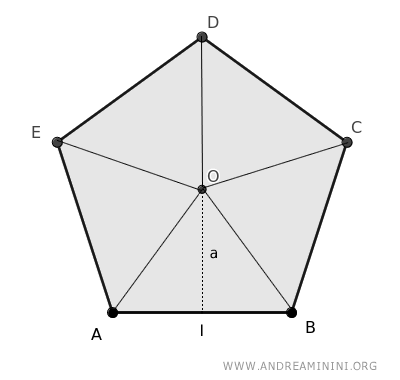
The area of each triangle is found by multiplying the base by the height and dividing by two, or in this case, multiplying the side of the polygon by the apothem and dividing by two.

The sum of the areas of these triangles equals the total area of the regular polygon.

The Radius of a Regular Polygon

The radius of a regular polygon is a segment that connects the center of the polygon to any of its vertices.

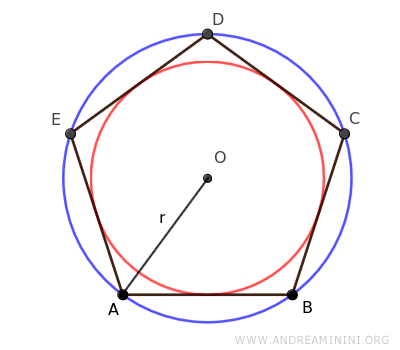
It is the radius of the circle circumscribed around the polygon since all vertices of a regular polygon lie on a circle whose center (O) is also the center of the polygon.

An interesting property of the radius is that, in a regular polygon, all the radii are congruent, meaning they all have the same length.

Additional Observations

Here are some additional notes on regular polygons:

• Symmetry
  Every regular polygon has both radial and axial symmetry. The number of axes of symmetry is equal to the number of sides.
• Diagonals
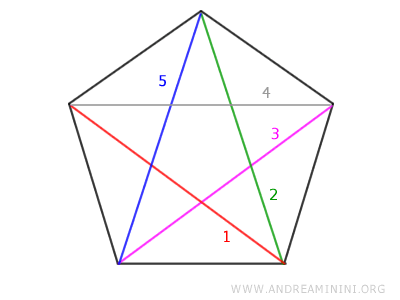
  The number of diagonals D in a regular polygon can be calculated using the formula $$ D=n(n−3)/2 $$ where n is the number of sides.

  Example. A pentagon has n=5 sides, so it has D=5 diagonals: $$ D = 5 \cdot (5-3)/2 = 5 \cdot 2/2 = 5 $$ To verify this, simply draw all the possible diagonals between the vertices of the pentagon. There are 5 diagonals.
  

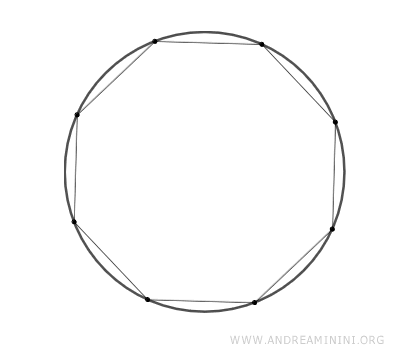
• As the number of sides increases, regular polygons progressively resemble a circle, while still remaining polygons with distinct sides, no matter how many sides they have.
  
• Inscribed and Circumscribed Circles
  A regular polygon can always be circumscribed around and inscribed in a circle.
  

  Note. In the special case of a regular hexagon, the side of the hexagon is always congruent to the radius of the inscribed circle.

• Equivalence Between a Regular Polygon and a Triangle
  The area of a regular polygon is equal to the area of a triangle with a base equal to the perimeter of the regular polygon and a height equal to the apothem of the regular polygon.
  
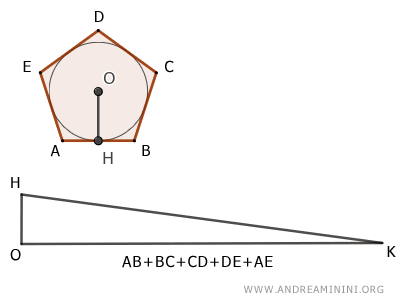
• Two Regular Polygons with the Same Number of Sides Are Similar Polygons
  This criterion simplifies the assessment of similarity between two polygons when they are regular and have the same number of sides.
  

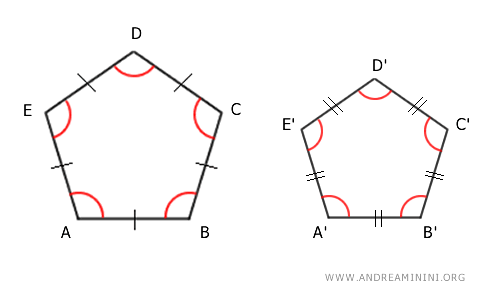
And so on.