Theorem of the Sum of Interior Angles in a Convex Polygon
In a convex polygon with n sides, the sum of the interior angles is equal to (n-2) straight angles (180° each). $$ (n-2) \cdot 180° $$
The sum of the interior angles in a convex polygon is determined by the number of sides it has.
For instance, a triangle has n=3 sides.
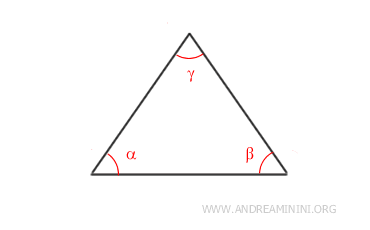
Thus, the sum of the interior angles in a triangle is 180°.
$$ (n-2) \cdot 180° $$
$$ (3-2) \cdot 180° = 180° $$
On the other hand, a rectangle has n=4 sides.
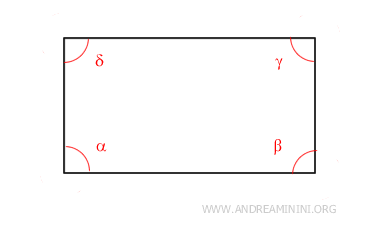
In this case, the sum of the interior angles of a rectangle is 360°.
$$ (n-2) \cdot 180° $$
$$ (4-2) \cdot 180° $$
$$ 2 \cdot 180° = 360° $$
A pentagon, with n=5 sides, works the same way.
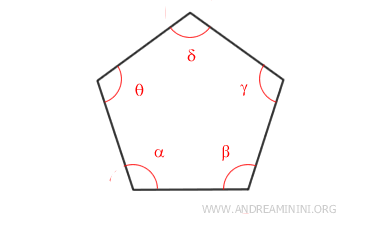
So, the sum of the interior angles is 540°.
$$ (n-2) \cdot 180° $$
$$ (5-2) \cdot 180° $$
$$ 3 \cdot 180° = 540° $$
This pattern applies to any polygon.
Proof of the Theorem
The proof is very straightforward.
Let’s consider any convex polygon with n sides - for instance, a polygon where n = 5.
The polygon can be either regular or irregular; that’s irrelevant. What matters is that it’s convex.
Now, pick any interior point $ P $ and connect it to each vertex of the polygon.
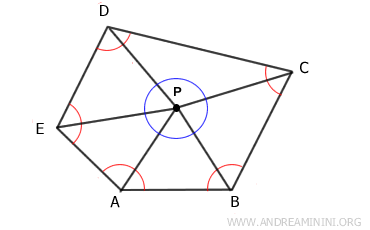
This construction divides the polygon into $ n $ triangles.
Since the sum of the interior angles of each triangle is 180°, the total sum of the polygon’s interior angles equals the sum of the interior angles of these $ n $ triangles, minus the angles surrounding point $ P $, which collectively add up to 360°.
$$ n \cdot 180° - 360° $$
A simple algebraic simplification yields:
$$ n \cdot 180° - 2 \cdot 180° $$
$$ (n - 2) \cdot 180° $$
And this confirms the original formula.
Note. In this case, with $ n = 5 $, the sum of the interior angles of a convex polygon with 5 sides is 540°: $$ (5 - 2) \cdot 180° = 3 \cdot 180° = 540° $$
Alternative Proof
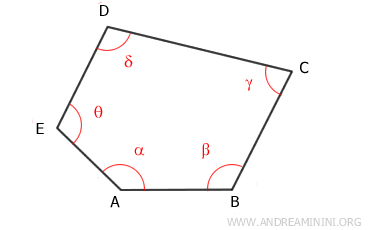
Once again, consider a convex polygon with n sides - for example, n = 5.

Pick any vertex and draw all possible diagonals from that point.
For example, let's choose vertex A.
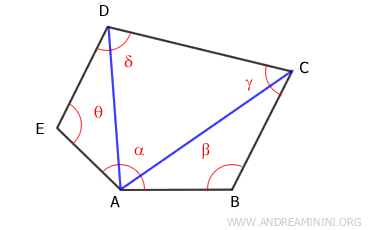
From a single vertex of the polygon, you can draw n-3 diagonals, dividing the polygon into n-2 triangles.
In this case, the convex polygon is split into three triangles: ADE, ACD, ABC.
$$ n - 2 = 5 - 2 = 3 \ \text{triangles} $$
This approach simplifies the original problem of calculating the sum of the interior angles by breaking it down into smaller, more manageable parts.
Since we know that the sum of the interior angles of a triangle is 180° and that the convex polygon is divided into three triangles, we can conclude that the sum of the interior angles of the convex polygon is 180° multiplied by three.
$$ 180° \cdot 3 = 540° $$
Therefore, the sum of the interior angles of a convex polygon with 5 sides is 540°.
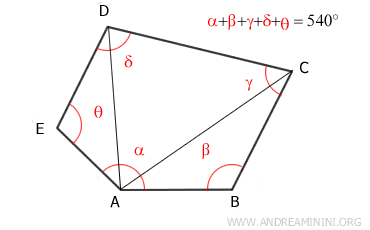
And this method can be applied to polygons with any number of sides.
