Trapezoid

A trapezoid is a quadrilateral with exactly two parallel sides.

The parallel sides are known as the trapezoid's bases.

Unlike other quadrilaterals with parallel sides, such as rectangles, in a trapezoid the bases are not congruent, meaning they have different lengths.

• Longer Base
  The longer base is the longer of the two parallel sides.
• Shorter Base
  The shorter base is the shorter of the two parallel sides.

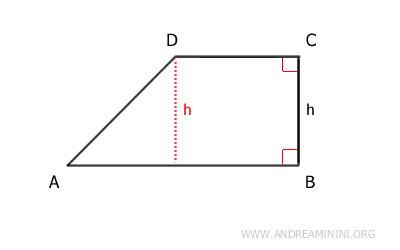
The perpendicular distance between the two bases is called the height of the trapezoid.

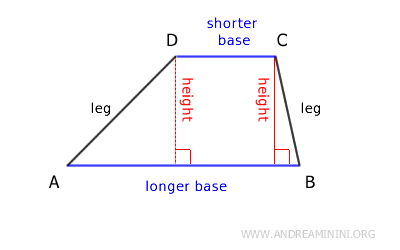
The other two sides, which are not parallel, are referred to as the legs.

A key property of the trapezoid is that the interior angles adjacent to each leg are supplementary, meaning their sum is 180° (a straight angle).

There are several types of trapezoids, including the right trapezoid, where one of the legs is perpendicular to the bases, the scalene trapezoid, where the legs have different lengths and neither is perpendicular to the bases, and the isosceles trapezoid, which has congruent legs.

Trapezoid Formulas

Here are the main formulas for calculating a trapezoid's dimensions:

• Perimeter
  The perimeter of a trapezoid is the sum of its legs and bases. $$ P = l_1+l_2+b_1+b_2 $$
• Trapezoid Area
  The area of a trapezoid is calculated by taking half the product of the sum of the bases and the height. $$ A = \frac{(a+b) \cdot h}{2} $$

Types of Trapezoids

There are three main types of trapezoids:

• Scalene Trapezoid
  A scalene trapezoid has legs of different lengths.
  
• Isosceles Trapezoid
  An isosceles trapezoid has congruent legs.
  
• Right Trapezoid
  A right trapezoid has one leg perpendicular to the bases, creating two right angles. In a right trapezoid, one leg coincides with the height.
  

The concept of the trapezoid has ancient origins, dating back to ancient Greece, where mathematicians like Euclid began to classify and study the properties of geometric figures. However, the distinction between different types of trapezoids, such as the scalene trapezoid, became clearer as geometry evolved over the centuries. For example, Euclid's definition of a trapezoid was simply a quadrilateral that is not a parallelogram. In Proclus's definition, however, a trapezoid is a quadrilateral with two parallel sides.

Additional Notes

Here are some additional observations about trapezoids:

• Each leg of a trapezoid can be considered a transversal intersecting two parallel lines
  This allows us to use properties of parallel lines, particularly the parallel lines theorem, to determine the interior angles of the trapezoid.
  
• The angles adjacent to each leg of a trapezoid are supplementary (180°)
  

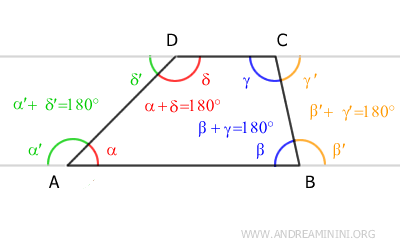
  Proof: The interior angles adjacent to a leg of the trapezoid can be considered as consecutive interior or exterior angles of a transversal intersecting two parallel lines. In this case, the parallel lines are the bases of the trapezoid (AB and CD), while the transversal is the line containing a leg of the trapezoid (AD or BC). According to the parallel lines theorem, consecutive interior or exterior angles are supplementary angles, meaning their sum is 180°.

• In an isosceles trapezoid, the angles adjacent to each base are congruent.
• In an isosceles trapezoid, the diagonals are congruent.

And so on.