Supplementary Angles

Supplementary angles are two angles whose sum is 180° (π radians).

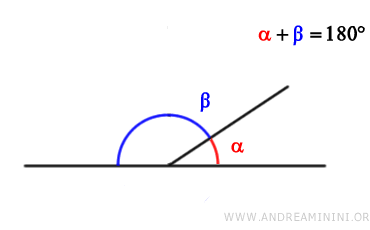
In simpler terms, two angles are "supplementary" if their sum equals a straight angle.

This is true regardless of the angles' position or orientation.

The concept of supplementary angles applies only to pairs of angles. Thus, a single angle cannot be supplementary; it takes two.

A Practical Example

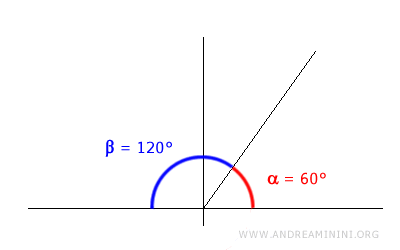
Consider the following two angles:

$$ \alpha = 60° $$

$$ \beta = 120° $$

These angles are supplementary because their measures add up to 180°.

$$ \alpha + \beta = 180° $$

The result of this addition is a straight angle.

Key Points

Supplementary angles have several interesting properties:

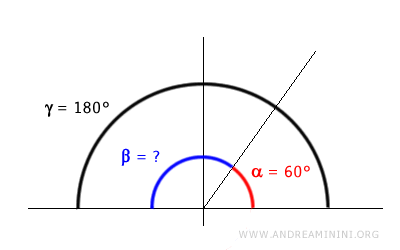
• Every angle has a supplementary angle
  Given any angle, you can find its supplementary angle by subtracting its measure from 180 degrees. For example, if angle alpha measures 120° $$ \alpha = 120° $$ then its supplementary angle beta is 60° $$ \beta = 180° - \alpha = 180° - 120° = 60° $$ Thus, for any given angle, you can always determine its supplementary angle by calculating the difference.
  
• When two lines intersect, consecutive angles taken in pairs are supplementary
  This property is frequently used in solving geometric problems and proving theorems.
  
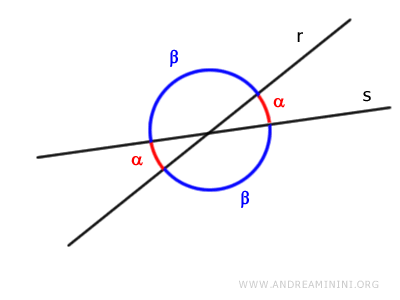
• Adjacent angles are always supplementary (and vice versa)
  Two angles are considered "adjacent" if they share a common side and the non-common sides are extensions of the same line. Therefore, to find the supplementary angle of a given angle, you just need to identify its adjacent angle.
  
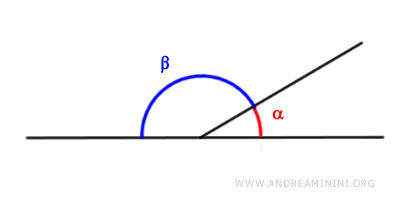
• Supplementary Angles of Two Congruent Angles
  If two angles, \( \alpha \) and \( \alpha' \), are supplementary to two congruent angles, \( \beta \cong \beta' \) (or to the same angle), then they must also be congruent: \( \alpha \cong \alpha' \).
  

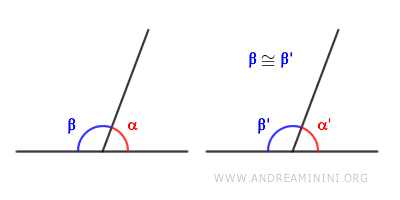
  Proof. Let \( \alpha \) and \( \alpha' \) be two angles, each supplementary to \( \beta \) and \( \beta' \), respectively. By definition, this means: $$ \alpha + \beta = 180^\circ $$ $$ \alpha' + \beta' = 180^\circ $$ Given that \( \beta \) and \( \beta' \) are congruent (\( \beta \cong \beta' \)), we can express \( \alpha \) and \( \alpha' \) as follows: $$ \alpha = 180^\circ - \beta $$ $$ \alpha' = 180^\circ - \beta' $$ Since \( \beta \) and \( \beta' \) are identical in measure, substituting \( \beta' \) for \( \beta \) in the first equation gives: $$ \alpha = 180^\circ - \color{red}{ \beta' } $$ $$ \alpha' = 180^\circ - \beta' $$ Because all straight angles (180°) are congruent, and we know \( \beta \cong \beta' \), it follows that \( \alpha \) and \( \alpha' \) must also be congruent. Hence, we conclude that: $$ \alpha \cong \alpha' $$ as required.

And so forth.