Postulate of Angle Divisibility

Any angle α with a non-zero measure can be divided into n>0 congruent parts.

Where n is any natural number.

The n-th part of the angle is a submultiple β of the angle itself.

$$ \beta = \frac{1}{n} \alpha $$

A Practical Example

Let's consider an angle α measuring 45°

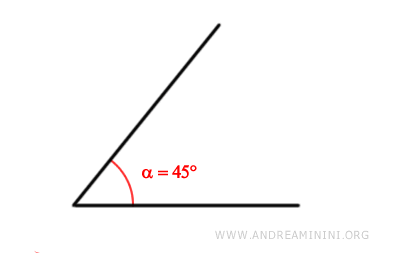
We divide the angle into n=3 equal parts.

$$ \beta = \frac{1}{3} \cdot 45° = 15° $$

Each part is an angle β of 15° and is a submultiple of the original angle α.

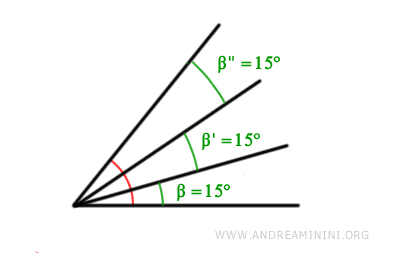
The sum of the three 15° angles gives us the original angle α (45°)

$$ 15° + 15° + 15° = 45° $$

In the same way, we can divide the angle α into any number of parts.

And so forth.