Measuring Angles in Degrees, Minutes, and Seconds
Angles can be measured in degrees (°), minutes (′), and seconds (″) using the following system: $$ 1 \ \text{degree (°)} = 60 \ \text{minutes (′)} $$ $$ 1 \ \text{minute (′)} = 60 \ \text{seconds (″)} $$
This is an alternative to the decimal degree system.
For example, an angle of 30° 15′ 20″ is read as:
- 30 degrees
- 15 minutes
- 20 seconds
This notation is widely used in navigation and cartography for measuring latitude and longitude, in astronomy for pinpointing stars and planets, and in geometry and trigonometry for angle calculations in triangles.
Note: While decimal degrees (e.g., 45.324°) are more convenient for mathematical calculations, degrees, minutes, and seconds remain valuable in fields where precision and readability are key. This system dates back to the Babylonians, who developed the sexagesimal (base-60) system due to its highly divisible nature. It was later adopted in navigation, map reading, and astronomy. Today, both systems are in use, with the choice depending on the specific application.
Converting Between Decimal Degrees and Degrees, Minutes, and Seconds
Angles are sometimes expressed in decimal form, such as 45.675°, and need to be converted to degrees, minutes, and seconds, or vice versa.
Converting Decimal Degrees to Degrees, Minutes, and Seconds
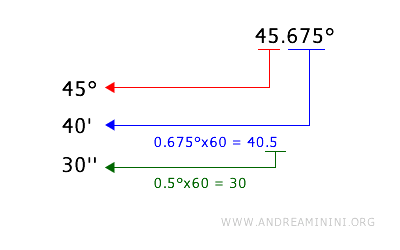
To convert a decimal degree measurement (e.g., 45.675°) to degrees, minutes, and seconds:
- The whole number represents the degree value (45°), which remains unchanged.
- Multiply the decimal portion by 60 to find the minutes: $$ 0.675 \times 60 = 40.5 $$ The whole number is the number of minutes (40′).
- Multiply the remaining decimal by 60 to find the seconds: $$ 0.5 \times 60 = 30 $$ The whole number is the number of seconds (30″).
- The final angle measurement is 45° 40′ 30″.
Converting Degrees, Minutes, and Seconds to Decimal Degrees
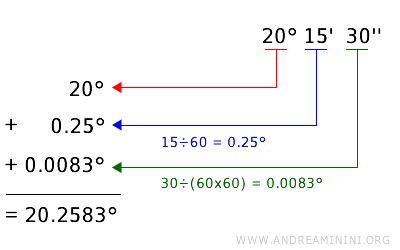
To convert an angle from degrees, minutes, and seconds (e.g., 20° 15′ 30″) to decimal degrees:
- Keep the degree value unchanged (20°).
- Convert the minutes to decimal degrees by dividing by 60: $$ 15′ = 15 \div 60 = 0.25° $$
- Convert the seconds to decimal degrees by dividing by 3600: $$ 30″ = 30 \div 3600 = 0.0083° $$
- Add all the values together: $$ 20° + 0.25° + 0.0083° = 20.2583° $$
- The final angle measurement in decimal degrees is 20.2583°.
And so on.
