Vertically Opposite Angles

Vertically opposite angles are two angles that share the same vertex, with each pair of sides extending from one another.

In other words, not only do they share the vertex, but the sides of the angles are aligned along the same straight lines.

A Practical Example

Let's draw two lines that intersect at a point P.

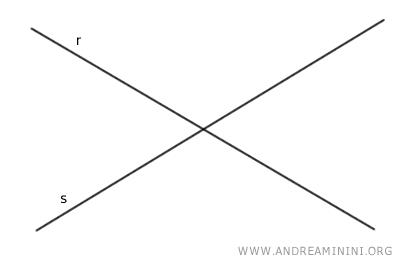
The lines create two vertically opposite angles, alpha and beta, at vertex P.

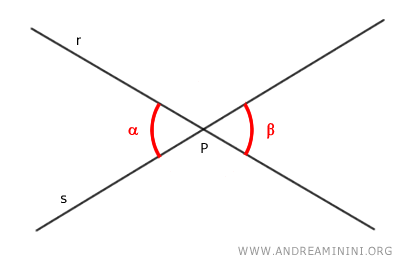
Observations

Here are some key points about vertically opposite angles:

• Vertically opposite angles are congruent.

  Proof. Consider the vertically opposite angles alpha and beta, and another angle gamma.
  
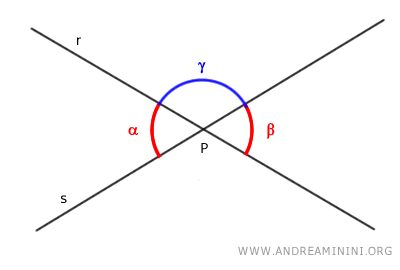
  The sum of angles alpha and gamma is 180°, forming a straight angle. Hence, alpha and gamma are adjacent angles. $$ \alpha + \gamma = 180° $$ Similarly, angles beta and gamma are adjacent because their sum is also 180°. $$ \beta + \gamma = 180° $$ Therefore, by solving the two equations for angles alpha and beta, we show that the two angles are congruent: $$ \alpha = 180° - \gamma $$ $$ \beta = 180° - \gamma $$

• Exterior Angles
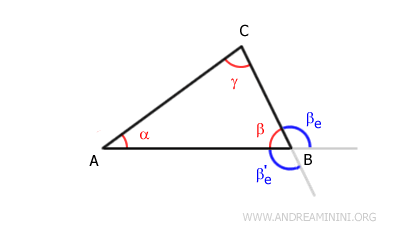
  In a polygon, two exterior angles (β_e and β'_e) at the same vertex (B) are vertically opposite and therefore congruent: β_e≅β'_e. Each of these angles is supplementary to the corresponding interior angle (β), meaning that β_e + β = 180° and β'_e + β = 180°. Because of this, the term "exterior angle" is generally used without distinguishing between the two.
  

And so on.