Angle Bisector

The angle bisector is a ray that starts at the vertex and divides the angle into two equal parts, creating two congruent angles.

For example, consider a 60° angle.

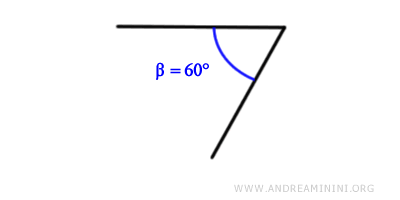
The bisector of this angle is a ray that begins at the vertex and splits the angle into two 30° angles.

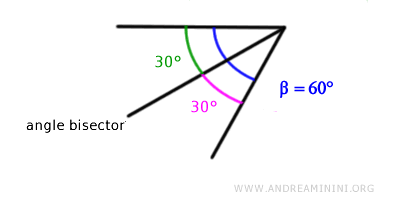
The Equation of the Angle Bisector

The equation that describes the bisectors of the angles formed by the intersection of two lines is: $$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$

This equation defines the two bisectors that result from dividing an angle into two equal parts.

The symbol ± indicates the presence of two distinct bisectors: one for the acute angle and one for the obtuse angle formed by the intersection of the two lines.

Example

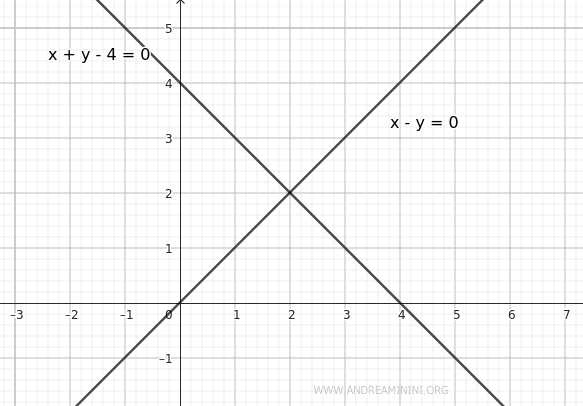
Consider the following line equations:

$$ r: \ x - y = 0 $$

$$ s: \ x + y - 4 = 0 $$

These are two intersecting lines.

We use the general equation for bisectors:

$$ \frac{ax + by + c}{\sqrt{a^2 + b^2}} = \pm \frac{a'x + b'y + c'}{\sqrt{a'^2 + b'^2}} $$

Substituting the coefficients of the two equations: a=1, b=-1, c=0 and a'=1, b'=1, c=-4

$$ \frac{x -y }{\sqrt{1^2 + (-1)^2}} = \pm \frac{x + y -4}{\sqrt{1^2 + 1^2}} $$

$$ \frac{x - y }{\sqrt{1+1}} = \pm \frac{x + y -4}{\sqrt{1 + 1}} $$

$$ \frac{x - y }{\sqrt{2}} = \pm \frac{x + y -4}{\sqrt{2}} $$

We eliminate the denominator \(\sqrt{2}\) since it is the same for both expressions:

$$ \frac{x - y }{\sqrt{2}} \cdot \sqrt{2} = \pm \frac{x + y -4}{\sqrt{2}} \cdot \sqrt{2} $$

$$ x - y = \pm ( x + y - 4 ) $$

Now, let's separate the two cases for the signs:

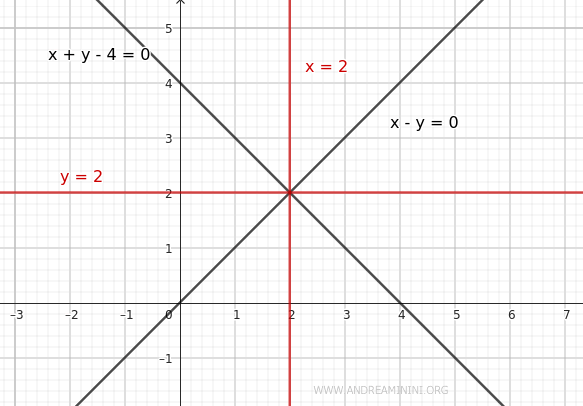
• For the positive sign (+): $$ x - y = x + y - 4 $$ Rearranging the terms: $$ -2y = -4 $$ Thus, the equation of one bisector is a line parallel to the y-axis: $$ y = 2 $$
• For the negative sign (-): $$ x - y = -(x + y - 4) $$ $$ x - y = -x - y + 4 $$ Rearranging the terms: $$ 2x = 4 $$ The other bisector is a line that, in this case, is parallel to the x-axis: $$ x = 2 $$

Therefore, the equations of the two bisectors for the angles formed by the lines are $ y = 2 $ and $ x = 2 $

Remarks

Some observations about the bisector:

• Every angle has one and only one bisector.
• Two intersecting lines form two pairs of congruent opposite angles and two bisectors perpendicular to each other.
  For example, if two lines r and s intersect forming an acute angle of 45°, the directly opposite angle will also be 45°. Since a straight angle measures 180°, the supplementary angle to 45° is an obtuse angle of 135° (180° - 45° = 135°), and its opposite angle is also 135°.
  
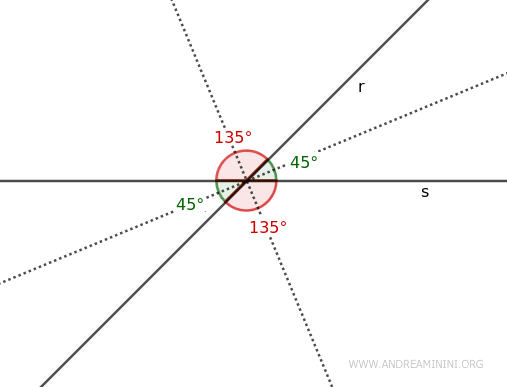
• Two opposite angles at the vertex share the same bisector.
• Points on the bisector are equidistant from the sides of the angle.
  The bisector of an angle is a geometric locus because any point on the bisector is equidistant from the sides of the angle.

  Proof. Consider any point P on the bisector r of the angle. Since the bisector divides the angle into two congruent angles α≅α'. Draw a segment OP that connects the vertex of the angle with point P on the bisector, and two perpendicular segments AP and BP from P to the sides of the angle. From these premises, we deduce that triangles OAP≡OBP are congruent by the second criterion of triangle congruence because they have two congruent angles and one congruent side (OP). Since the triangles are congruent, all their sides are congruent. Therefore, the sides AP≡BP are congruent. This proves that any point P on the bisector is equidistant from the sides of the angle.
  
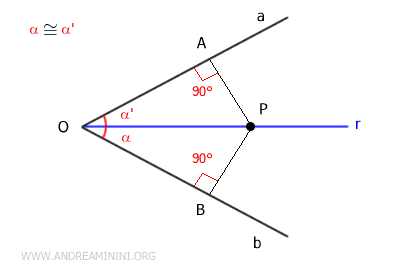
  Reverse Proof. In this case, we must prove that any point P equidistant from the sides of the angle is a point on the bisector. By the initial hypothesis, consider a point P equidistant from the sides of the angle AP≡BP and a bisector r. The distance of a point from a segment is the length of the perpendicular segment from the point P to the segment. Thus, the distance AP is perpendicular to side "a" while the distance BP is perpendicular to side "b". The right triangles OAP≡OBP are congruent by the criteria for right triangle congruence, as the legs AP≡BP and the hypotenuse OP are congruent. Being congruent, the two triangles have all sides and angles congruent. Particularly, we are interested in the congruent angles α≡α' of triangles OAP and OBP, as this indicates that the hypotenuse OP and the point P belong to the bisector r of the angle. Therefore, if a point P is equidistant from the sides of an angle, it is a point on the bisector r of the angle.

And so on.