Equation of an Angle Bisector

The angle bisector is the ray that starts from the vertex of an angle, dividing it into two equal angles. The equation for the bisector is:

$$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$

This equation represents the two bisectors that split an angle into two congruent angles.

The ± sign indicates that there are two bisectors: one dividing the acute angle and the other dividing the obtuse angle formed by the intersection of the two lines.

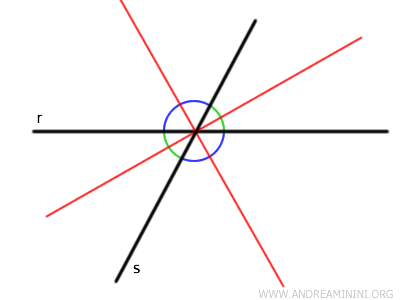
Note: This formula is based on the fact that points on the bisector are equidistant from the two lines. The bisector is the locus of points that are equally distant from both lines.

A Practical Example

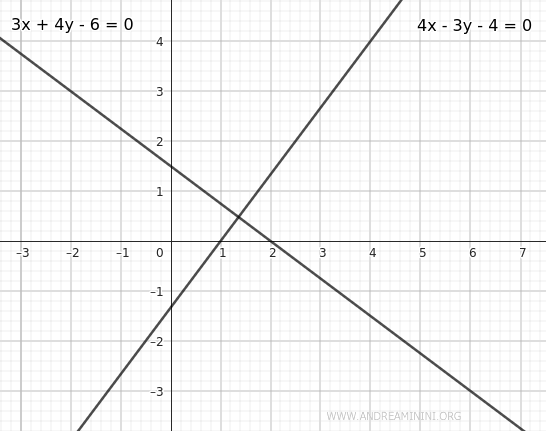
Let's consider the equations of two non-parallel lines:

$$ r : 3x+4y-6=0 $$

$$ s: 4x-3y-4=0 $$

The two lines intersect, forming two pairs of congruent angles: one pair of acute angles and one pair of obtuse angles.

To find the equations of the two bisectors, we use the following formula:

$$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$

Substituting the coefficients of the lines r and s, we have a=3, b=4, c=-6 and a'=4, b'=-3, c'=-4.

$$ \frac{3x+4y-6}{ \sqrt{3^2+4^2}} = \pm \frac{4x-3y-4}{ \sqrt{4^2+(-3)^2}} $$

$$ \frac{3x+4y-6}{ \sqrt{9+16}} = \pm \frac{4x-3y-4}{ \sqrt{16+9}} $$

$$ \frac{3x+4y-6}{ \sqrt{25}} = \pm \frac{4x-3y-4}{ \sqrt{25}} $$

$$ \frac{3x+4y-6}{ 5 } = \pm \frac{4x-3y-4}{ 5} $$

Using the invariant property of equations, we multiply both sides by 5 and simplify:

$$ \frac{3x+4y-6}{ 5 } \cdot 5 = \pm \frac{4x-3y-4}{ 5} \cdot 5 $$

$$ 3x+4y-6 = \pm (4x-3y-4) $$

Now, let's consider each case separately, where the sign in the second term is either positive or negative.

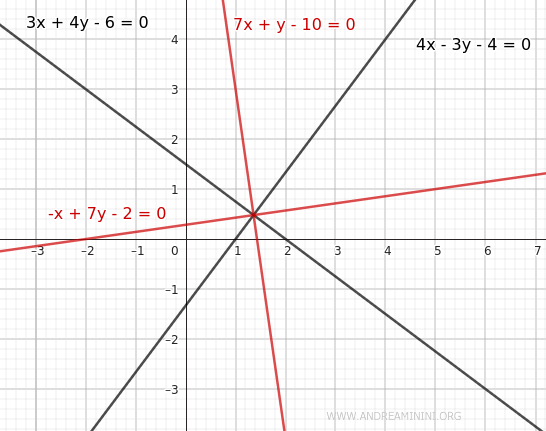
• Case 1 (+): $$ 3x+4y-6 = + (4x-3y-4) $$ $$ 3x+4y-6 - 4x + 3y + 4 = 0 $$ This simplifies to the equation of one bisector: $$ -x+7y-2 = 0 $$
• Case 2 (-): $$ 3x+4y-6 = - (4x-3y-4) $$ $$ 3x+4y-6 = -4x+3y+4 $$ $$ 3x+4y-6 + 4x - 3y - 4 = 0 $$ This simplifies to the equation of the other bisector: $$ 7x+y-10 = 0 $$

Thus, we have found the equations of the bisectors for the two pairs of opposite angles.

The Proof

An angle is formed between two rays r and s, called the "sides" of the angle, originating from a point known as the "vertex" of the angle.

Consider the equations of the two lines:

$$ r: \ ax+by+c=0 $$

$$ s: \ a'x+b'y+c'=0 $$

The angle bisector is a ray that starts from the vertex of the angle and has the property that every point on it is equidistant from the sides of the angle.

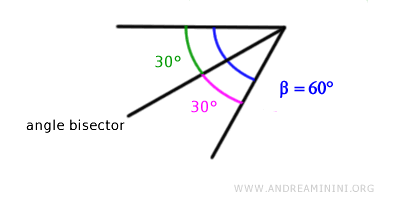
Thus, the bisector is the locus of points that are equidistant from the sides of the angle.

For example, if we consider point P on the bisector, the distance from P to line r is the segment $ \overline{AP} $ perpendicular to r with endpoint P and a point A on line r. Similarly, the distance from P to line s is the segment $ \overline{BP} $.

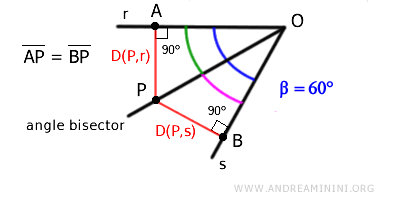
Point P is equidistant from both lines only if the segments $ \overline{AP} \cong \overline{BP} $ are congruent, meaning the segments $ \overline{AP} $ and $ \overline{BP} $ have the same length.

$$ \overline{AP} \cong \overline{BP} $$

Therefore, points that are equidistant satisfy the equation:

$$ D(P,r) = D(P,s) $$

The formula that measures the distance D(P,r) of a point P(x;y) from line r is as follows:

$$ D(P,r) = \frac{|ax+by+c|}{ \sqrt{a^2+b^2}} $$

The formula that measures the distance D(P,s) from line s is:

$$ D(P,s) =\frac{|a'x+b'y+c'|}{ \sqrt{a'^2+b'^2}} $$

Note: It is important to remember that distances are expressed in absolute value because distance is the length of a segment and must always be a non-negative value.

Substitute the distance formulas D(P,r) and D(P,s) into the equality:

$$ D(P,r)=D(P,s) $$

$$ \frac{|ax+by+c|}{ \sqrt{a^2+b^2}} = \frac{|a'x+b'y+c'|}{ \sqrt{a'^2+b'^2}} $$

However, the reasoning is not yet complete, because when two lines intersect, they form four angles, or two pairs of opposite and congruent angles.

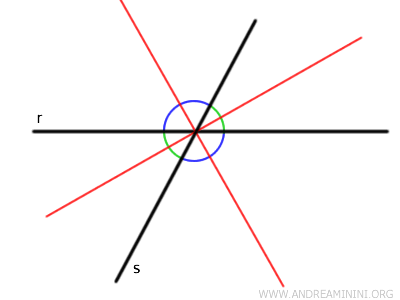
Thus, the bisectors to consider are two lines perpendicular to each other. One bisector divides the acute angle, while the other divides the obtuse angle.

To find both bisector equations, remove the absolute value on the left side of the equation and consider both possible signs on the right side:

$$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$

This demonstrates the formula for the equation of the bisector of the angles formed by two lines.

And so on.