Parabola Equation

The standard form of a parabola's equation, with its axis of symmetry parallel to the y-axis, is: $$ y = ax^2 + bx + c $$ where a, b, and c are real constant coefficients, and a is not equal to zero (a≠0).

The coefficient "a" plays a crucial role in the study of a parabola.

The absolute value |a| of the coefficient "a" determines the width of the parabola. The greater the value of |a|, the narrower the parabola appears relative to its axis.

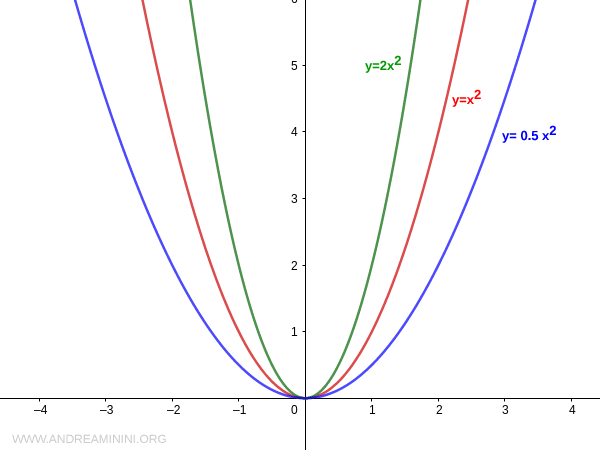
Moreover, the sign of the coefficient "a" determines the direction of the parabola's concavity.

• If a>0, the parabola opens upwards (convex).
• If a<0, the parabola opens downwards (concave).

When the parabola's axis of symmetry is horizontal, the standard form of the equation is: $$ x = ay^2 + by + c $$

The key components of a parabola are:

• Focus
  The focus \( F \) is a fixed point inside the parabola. Its coordinates are given by:
  \[ F \begin{pmatrix} -\frac{b}{2a}, \frac{1-\Delta}{4a} \end{pmatrix} \] where \( a \), \( b \), and \( c \) are the coefficients of the parabola's equation \( y = ax^2 + bx + c \), and the discriminant is \( \Delta = b^2 - 4ac \).
• Directrix
  The directrix \( d \) is a fixed line outside the parabola. Its equation is: $$ y= - \frac{1+\Delta}{4a} $$
• Axis
  The axis of a parabola is a line perpendicular to the directrix \( d \) and passing through the focus \( F \). It also acts as the axis of symmetry, dividing the parabola into two mirror-image halves. The equation of the axis is: $$ x = - \frac{b}{2a} $$
• Vertex
  The vertex \( V \) is the point where the parabola intersects its axis of symmetry. At the vertex, the parabola reaches its maximum or minimum value, depending on the sign of the coefficient \( a \) in the equation \( y = ax^2 + bx + c \). The coordinates of the vertex are given by: \[ V \left( -\frac{b}{2a} , -\frac{\Delta}{4a} \right) \] where \(\Delta = b^2 - 4ac\) is the discriminant.

Special Cases of the Parabola Equation

The equation of the parabola \( y= ax^2+bx+c \) can present special cases when the coefficients b and/or c are zero.

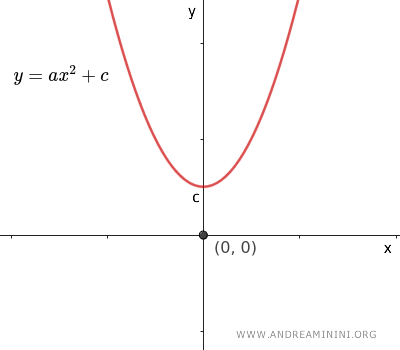
• If \( b=0 \), the equation becomes \( y=ax^2+c \), and the axis of the parabola coincides with the y-axis.
  
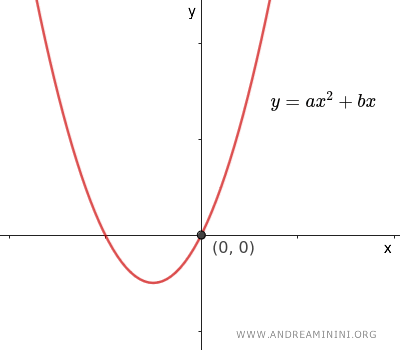
• If \( c=0 \), the equation becomes \( y=ax^2+bx \), and the graph of the parabola always passes through the origin O(0,0) of the Cartesian plane, because when x=0, y also equals 0.
  
• If \( b=0 \) and \( c=0 \), the equation simplifies to \( y =ax^2 \), making the axis of the parabola coincide with the y-axis, and its vertex coincide with the origin O(0,0) of the Cartesian plane.
  

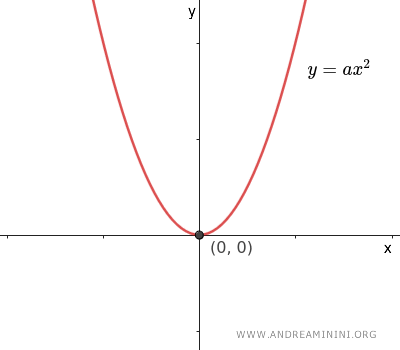
Equation of a Parabola with the Axis on the Y-axis and Vertex at the Origin

The equation of a parabola with its axis aligned with the y-axis and its vertex at the origin of the Cartesian plane is given by: $$ y = ax^2 $$ where the coefficient $ a \ne 0 $ is non-zero.

In this case, the axis of the parabola is simply:

$$ x = 0 $$

The focus F is located at the coordinates:

$$ F \left(0; \frac{1}{4a} \right) $$

The equation of the directrix is:

$$ y = - \frac{1}{4a} $$

Note: The equation of a parabola with its axis on the y-axis and its vertex at the origin has all non-negative values if the coefficient $a > 0$. In this case, the focus is also positive, and the parabola opens upwards. Conversely, it has all non-positive values if $a < 0$. In this case, the focus is negative, and the parabola opens downwards.

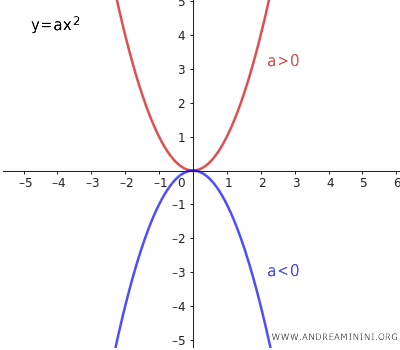
Two parabolas are "symmetric parabolas" when they have opposite coefficients "a". For example, $ y = \frac{1}{8} x^2 $ and $ y = - \frac{1}{8} x^2 $ are symmetric parabolas. Symmetric parabolas are also congruent. In the particular case where $a = 0$, the parabola degenerates into a line $y = 0$ that coincides with the x-axis. These are called "degenerate parabolas."

Example

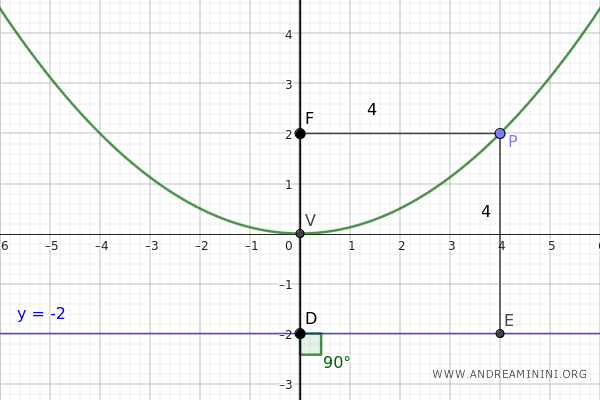
In this example, we consider the parabola:

$$ y = \frac{1}{8} x^2 $$

The coefficient $ a = \frac{1}{8} $, so the focus of the parabola is located at the following coordinates:

$$ F \left(0; \frac{1}{4a} \right) $$

$$ F \left(0; \frac{1}{4 \cdot \frac{1}{8}} \right) $$

$$ F \left(0; \frac{1}{\frac{1}{2}} \right) $$

$$ F (0; 2) $$

The equation of the directrix is:

$$ y = - \frac{1}{4a} $$

$$ y = - \frac{1}{4 \cdot \frac{1}{8} } $$

$$ y = - \frac{1}{ \frac{1}{2} } $$

$$ y = - 2 $$

Here is the graph of the parabola:

Proof

We start by assuming the axis of the parabola coincides with the y-axis and the vertex V is at the origin of the Cartesian plane.

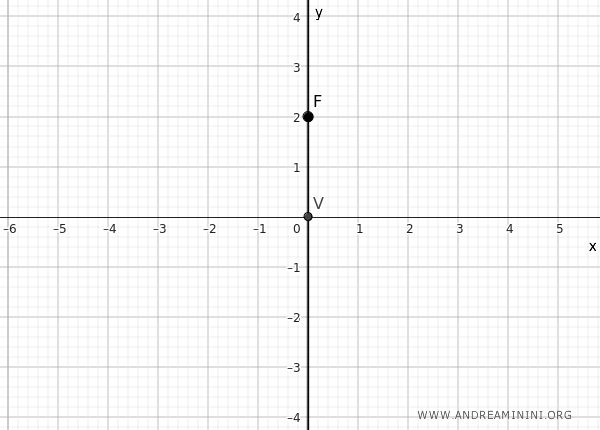
The focus F is a point on the axis of the parabola, which in this case is a point on the y-axis.

In a parabola, the distance between the focus and any point on the parabola is equal to the distance between the directrix and that same point.

In this case, point V is the only known point on the parabola, but we can deduce that the distance VF is congruent to OD, where D is a point on the directrix.

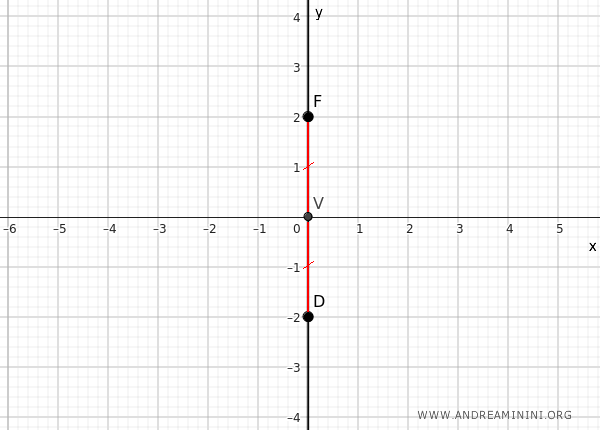
Knowing that the directrix is always perpendicular to the axis of the parabola, we deduce that in this case, the directrix is parallel to the x-axis and passes through point D.

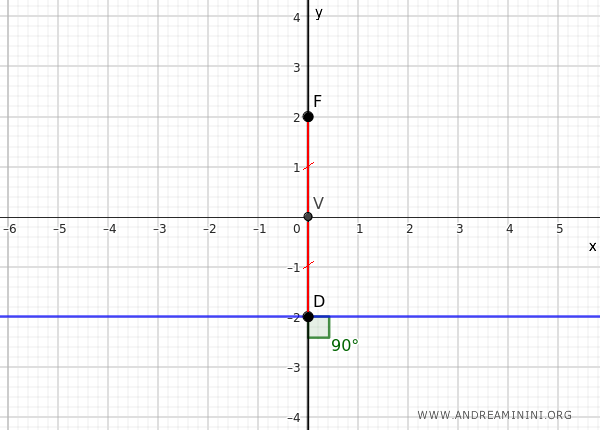
Therefore, the equation of the directrix is:

$$ y = -f $$

Where f=VD and =VF by construction since VD=VF.

Now, let's take any point P on the parabola.

By definition, the distance PF between the point and the focus must be equal to the distance PE between the point and the directrix, that is, PF=PE.

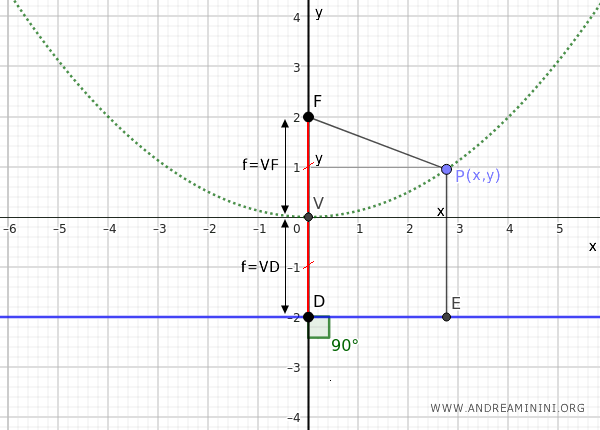
The segment PF is congruent to the segment PE:

$$ \overline{PF} = \overline{PE} $$

We can write the segment PF as the Euclidean distance between two points: $ \overline{PF} = \sqrt{ x^2 + (f-y)^2 }$ where $f=VF$.

$$ \sqrt{ x^2 + (f-y)^2 } = \overline{PE} $$

We can write the segment PE as the sum $ \overline{PE} = | y + f | $ where $f=VD$.

$$ \sqrt{ x^2 + (f-y)^2 } = | y+f | $$

We apply the invariant property of equations and square both sides of the equation:

$$ \left( \sqrt{ x^2 + (f-y)^2 } \right)^2 = ( | y+f | )^2 $$

$$ x^2 + (f-y)^2 = ( y+f )^2 $$

$$ x^2 + f^2 -2fy + y^2 = y^2 + 2fy + f^2 $$

$$ x^2 -2fy -2fy = 0 $$

$$ x^2 -4fy = 0 $$

This allows us to solve for y and obtain the equation of the parabola:

$$ y = \frac{1}{4f} x^2 $$

By setting the coefficient $ a= \frac{1}{4f} $, the equation becomes:

$$ y = ax^2 $$

Since \( f \ne 0 \) to avoid division by zero, it follows that \( a \ne 0 \). Consequently, the coefficient \( a \) must always be non-zero.

From the relation $ a= \frac{1}{4f} $, we can also derive the y-component $f$ of the focus coordinates $F(x,y)$:

$$ f = \frac{1}{4a} $$

In this case, the axis of the parabola coincides with the y-axis, so the x-component is zero.

Therefore, the focus is at these coordinates on the Cartesian plane:

$$ F(x,y) = \left( 0, \frac{1}{4a} \right) $$

Finally, knowing that the directrix is:

$$ y = -f $$

We substitute $ f=\frac{1}{4a} $ to get the full equation of the directrix:

$$ y = -\frac{1}{4a} $$

In this way, we have derived all the formulas for the equation of a parabola with its axis along the y-axis and its vertex at the origin of the Cartesian plane.

Equation of a Parabola with Axis Parallel to the Y-axis

The equation of a parabola with an axis parallel to the y-axis and a vertex at any point in the plane is given by the following, where the coefficient $ a \ne 0 $ is non-zero: $$ y = ax^2 + bx + c $$ Alternatively, the equation of the parabola can be expressed in the general form, where (h, k) is the vertex: $$ y =a (x-h)^2 + k $$ or in the standard form, where p is the distance from the focus to the vertex: $$ (x-h)^2 = 4p(y-k)  $$

Any parabola $ y= ax^2 +bx+c $ with its axis parallel to the y-axis and its vertex at the point $ V (x_v; y_v ) $ is obtained by translating a parabola $ y = ax^2 $ with its vertex at the origin and axis along the y-axis.

$$ y - y_v = a(x - x_v)^2 $$

The axis of the parabola is:

$$ x = - \frac{b}{2a} $$

The vertex of the parabola is at the following coordinates:

$$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{\Delta}{4a} \end{pmatrix} $$

Where a, b, and c are the coefficients of the parabola's equation $y=ax^2+bx+c$ and the discriminant Δ=b²-4ac.

The focus F is located at the coordinates:

$$ F \begin{pmatrix} - \frac{b}{2a} \ , \ \frac{1-\Delta}{4a} \end{pmatrix} $$

The equation of the directrix is:

$$ y= - \frac{1+\Delta}{4a} $$

Note: Every equation of the form $ y=ax^2+bx+c $ with $ a \ne 0 $ corresponds to a parabola with its axis parallel to the y-axis and vice versa. This is because parabolas with their axes parallel to the y-axis are simply translations of the parabolas $y=ax^2$ with their axes along the y-axis.

Example

Consider the following parabola:

$$ y = 2x^2 - 4x - 1 $$

The vertex of the parabola is at coordinates V where $a=2$, $b=-4$, $c=-1$, and the discriminant is $ \Delta=b^2- 4ac $.

$$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{\Delta}{4a} \end{pmatrix} $$

$$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{b^2-4ac}{4a} \end{pmatrix} $$

$$ V \begin{pmatrix} - \frac{-4}{2 \cdot 2} \ , \ - \frac{(-4)^2-4 \cdot 2 \cdot (-1) }{4 \cdot 2} \end{pmatrix} $$

$$ V \begin{pmatrix} \frac{4}{4} \ , \ - \frac{16+8 }{8} \end{pmatrix} $$

$$ V \begin{pmatrix} 1 \ , \ - \frac{24}{8} \end{pmatrix} $$

$$ V \begin{pmatrix} 1 \ , \ - 3 \end{pmatrix} $$

The directrix is as follows, knowing already that Δ=b²-4ac=24 and $a=2$:

$$ y= - \frac{1+\Delta}{4a} $$

$$ y= - \frac{1+24}{4 \cdot 2} $$

$$ y= - \frac{25}{8} $$

The focus is at the coordinates, knowing already that Δ=b²-4ac=24, $a=2$, and $b=-4$:

$$ F \begin{pmatrix} - \frac{b}{2a} \ , \ \frac{1-\Delta}{4a} \end{pmatrix} $$

$$ F \begin{pmatrix} - \frac{-4}{2 \cdot 2} \ , \ \frac{1-24}{4 \cdot 2} \end{pmatrix} $$

$$ F \begin{pmatrix} 1 \ , \ \frac{-23}{8} \end{pmatrix} $$

For confirmation, here is the graph of the parabola, where each point on the parabola is equidistant from the focus F and the directrix:

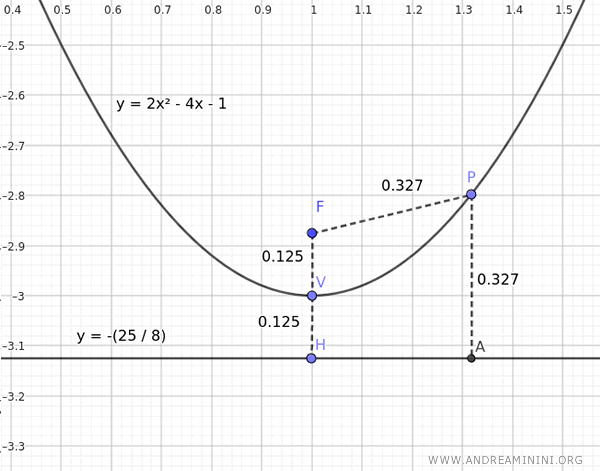
Note: The distance between the origin O(0,0) of the Cartesian plane and the vertex of the parabola $ V \begin{pmatrix} 1 \ , \ - 3 \end{pmatrix} $ is the vector $ \vec{v} = \begin{pmatrix} 1 \ , \ - 3 \end{pmatrix} $.

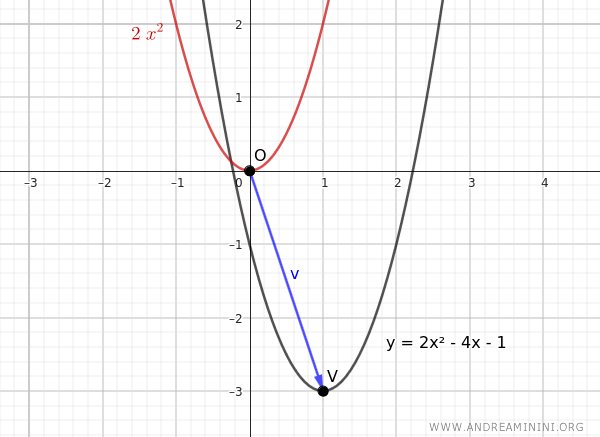
Therefore, we can show that the parabola $ y=2x^2 -4x-1 $ is a translation of another parabola passing through the origin $ y = 2x^2 $ with the same coefficient $ a =2 $. $$ y - y_v = a(x - x_v)^2 $$ $$ y - y_v = 2(x - x_v)^2 $$ In this case, the vertex V(1,-3) has components $x_v = 1$ and $y_v = -3$: $$ y - (-3) = 2(x - 1)^2 $$ $$ y + 3 = 2(x-1)^2 $$ $$ y = 2(x-1)^2 -3 $$ $$ y = 2(x^2-2x+1) -3 $$ $$ y = 2x^2-4x+2 -3 $$ $$ y = 2x^2-4x-1 $$ This confirms that the parabola $ y=2x^2 -4x-1 $ is a translation of the parabola passing through the origin $ y = 2x^2 $. These two parabolas are congruent as they can be overlaid point by point after a rigid movement, that is, an isometric transformation that causes no distortion.

Proof

To prove the equation $ y=ax^2+bx+c $, we start with the following hypothesis:

Every parabola with its axis parallel to the y-axis is a translation of a parabola $ y=ax^2 $ with its axis along the y-axis.

$$ y = ax^2 $$

In general, the translation of any point $ (x;y) \rightarrow (x';y') $ in the plane is obtained through the following isometric operation:

$$ \begin{cases} x' = x + x_v \\ \\ y' = y + y_v \end{cases} $$

Where $(x;y)$ are the coordinates of the original point, and $(x';y')$ are the coordinates of the translated point.

The terms $x_v$ and $ y_v $ are the components of the translation vector $ \vec{v} = \begin{pmatrix} x_v \\ y_v \end{pmatrix} $.

We derive the variables $x$ and $y$ from these equations:

$$ \begin{cases} x = x' - x_v \\ \\ y= y' - y_v \end{cases} $$

We substitute $x$ and $y$ in the equation of the parabola with its vertex at the origin:

$$ y = ax^2 $$

$$ y' - y_v = a(x' - x_v)^2 $$

We eliminate the primes from the variables $x'$ and $y'$ used to distinguish them from those of the parabola $y=ax^2$.

This gives us the equation of a parabola with its axis parallel to the y-axis and its vertex at the point $ V (x_v; y_v ) $:

$$ y - y_v = a(x - x_v)^2 $$

We perform the algebraic calculations to solve for $y$:

$$ y = a (x^2 - 2xx_v + x_v^2) + y_v $$

$$ y = ax^2 - 2axx_v + ax_v^2 + y_v $$

We assign the coefficients $ b = - 2ax_v $ and $ c =ax_v^2 + y_v $ to obtain the equation of the parabola:

$$ y = ax^2 + bx +c $$

This proves that every equation of a parabola with its axis parallel to the y-axis can be expressed as a second-degree equation $ y = ax^2 + bx +c $.

From the coefficient $ b = - 2ax_v $, we derive the x-component $ x_v $ of the vertex coordinates:

$$ b = - 2ax_v $$

$$ x_v = - \frac{b}{2a} $$

From the coefficient $ c =ax_v^2 + y_v $, we derive the y-component $ y_v $ of the vertex coordinates:

$$ c =ax_v^2 + y_v $$

$$ y_v = c - ax_v^2 $$

$$ y_v = c - a \left( - \frac{b}{2a} \right)^2 $$

$$ y_v = c - a \left( -1 \cdot \frac{b}{2a} \right)^2 $$

$$ y_v = c - a \left( -1^2 \cdot \frac{b}{2^2a^2} \right) $$

$$ y_v = c - a \left( 1 \cdot \frac{b^2}{4a^2} \right) $$

$$ y_v = c - a \frac{b^2}{4a^2} $$

$$ y_v = c - \frac{b^2}{4a} $$

$$ y_v = \frac{4ac - b^2}{4a} $$

Knowing that the discriminant of a second-degree equation is $ \Delta = b^2-4ac $, we have $ - \Delta = 4ac - b^2 $:

$$ y_v = \frac{ - \Delta }{4a} $$

$$ y_v = - \frac{ \Delta }{4a} $$

Note: To prove that every equation $ y = ax^2 + bx +c $ is a parabola, we simply translate the equation $ y =ax^2 $ with a displacement vector $ \vec{v} = ( x_v ; y_v ) $: $$ y = ax^2 $$ $$ y + y_v = a(x+x_v)^2 $$ Knowing that $ x_v = - \frac{b}{2a} $ and $ y_v = - \frac{ \Delta }{4a} $: $$ y - \frac{ \Delta }{4a} = a(x - \frac{b}{2a})^2 $$ $$ y = a[x^2-2x\frac{b}{2a}+ (\frac{b}{2a})^2] + \frac{ \Delta }{4a} $$ $$ y = ax^2-2ax\frac{b}{2a}+ a \cdot \frac{b^2}{4a^2} + \frac{ \Delta }{4a} $$ $$ y = ax^2 - x b + \frac{b^2}{4a} + \frac{ \Delta }{4a} $$ Where $ \Delta = b^2-4ac $: $$ y = ax^2 - x b + \frac{b^2}{4a} + \frac{ b^2-4ac }{4a} $$ $$ y = ax^2 - x b + \frac{b^2}{4a} + \frac{ b^2 }{4a} - \frac{ 4ac }{4a} $$ $$ y = ax^2 - x b + 2 \cdot \frac{b^2}{4a} - c $$ $$ y = ax^2 - x b + \frac{b^2}{2a} - c $$ This last equation is a parabola. In fact, if we consider $ b' = -b $ and $ c' = \frac{b^2}{2a} - c $, we obtain the standard form of a parabola equation: $$ y = ax^2 + b'x + c' $$ This proves that the translation of the parabola $ y = ax^2 $ allows us to obtain any parabola parallel to the y-axis, represented by an equation in the form $ y=ax^2+bx+c $.

Equation of a Parabola with Axis Parallel to the X-axis

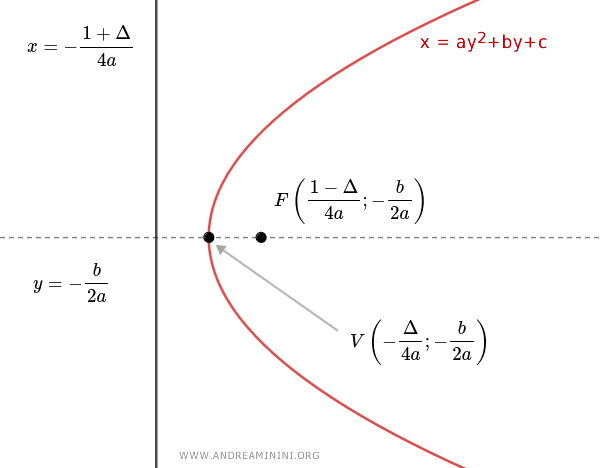
The equation of a parabola with its axis parallel to the x-axis and the vertex at any point in the plane is as follows, with the coefficient \( a \ne 0 \): $$ x = ay^2 + by + c $$ Alternatively, the equation of the parabola can be written in the general form where \((h,k)\) is the vertex: $$ x = a (y-k)^2 + h $$ or in the standard form where \( p \) is the distance from the focus to the vertex: $$ (y-k)^2 = 4p(x-h) $$

The central symmetry axis of the parabola is:

$$ y = - \frac{b}{2a} $$

The equation of the directrix is:

$$ x = - \frac{1+ \Delta}{4a} $$

Where the discriminant is $ \Delta = b^2-4ac $.

The focus of the parabola is located at the coordinates:

$$ F \left( \frac{1- \Delta}{4a}; - \frac{b}{2a} \right) $$

The vertex is at the coordinates:

$$ V \left( - \frac{\Delta}{4a}; - \frac{b}{2a} \right) $$

Summary:

Note: In this case, the sign of the coefficient "a" also determines the concavity of the parabola. If $a > 0$, the concavity is towards the positive x-axis. If $a < 0$, it is towards the negative x-axis. Additionally, the absolute value of the coefficient "a" determines the width of the parabola relative to its symmetry axis.

Example

Consider the following parabola:

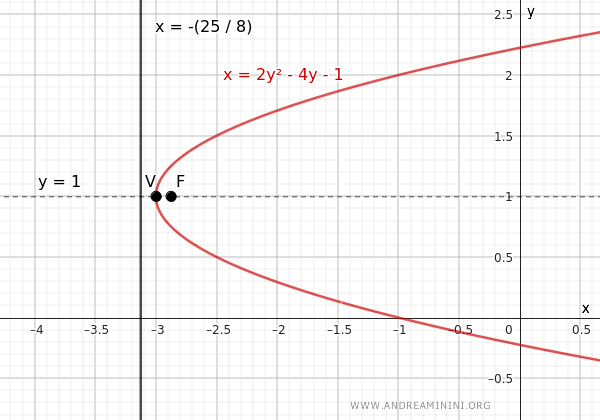
$$ x = 2y^2 - 4y - 1 $$

The coefficients of the parabola are $a=2$, $b=-4$, $c=-1$, and the discriminant is $ \Delta=24$.

$$ \Delta=b^2- 4ac = (-4)^2-4 \cdot 2 \cdot (-1) = 16+8 = 24 $$

The central symmetry axis of the parabola is:

$$ y = - \frac{b}{2a} $$

$$ y = - \frac{-4}{2 \cdot 2} $$

$$ y = \frac{4}{4} $$

$$ y = 1 $$

The directrix of the parabola is:

$$ x = - \frac{1+ \Delta}{4a} $$

$$ x = - \frac{1+ 24}{4 \cdot 2} $$

$$ x = - \frac{25}{8} $$

The focus of the parabola is located at the coordinates:

$$ F \left( \frac{1- \Delta}{4a}; - \frac{b}{2a} \right) $$

$$ F \left( \frac{1- 24}{4 \cdot 2}; - \frac{-4}{2 \cdot 2} \right) $$

$$ F \left( \frac{- 23}{8}; 1 \right) $$

The vertex is at the coordinates:

$$ V \left( - \frac{\Delta}{4a}; - \frac{b}{2a} \right) $$

$$ V \left( - \frac{24}{4 \cdot 2}; - \frac{-4}{2 \cdot 2} \right) $$

$$ V \left( - \frac{24}{8}; - \frac{-4}{4} \right) $$

$$ V \left( - 3; 1 \right) $$

Here is the graph of the parabola for visual confirmation:

Proof

Consider a parabola with its axis parallel to the y-axis:

$$ y=ax^2+bc+c $$

To transform it into a parabola with its axis parallel to the x-axis, we apply axial symmetry with respect to the bisector of the first and second quadrants of the Cartesian plane:

$$ \begin{cases} x' = y \\ \\ y' =x \end{cases} $$

Where $x'$ and $y'$ are the coordinates of the points on the parabola after the transformation, and $x$ and $y$ are the original coordinates.

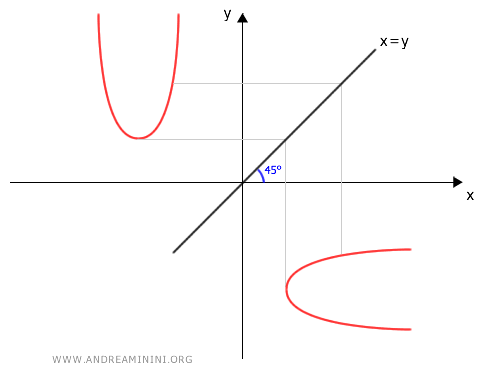
We apply the symmetry to the equation of the parabola with its axis parallel to the y-axis:

$$ y=ax^2+by+c $$

We substitute $x'=y$ and $y'=x$:

$$ x'=ay'^2+by'+c $$

Since we used $x'$ and $y'$ as variables for distinction from the original coordinates, we can now remove the primes:

$$ x=ay^2+by+c $$

We have thus obtained the equation of a parabola with its axis parallel to the x-axis.

The formulas for calculating the coordinates of the vertex, focus, directrix, etc., are obtained similarly. We apply axial symmetry with respect to the bisector of the first and third quadrants.

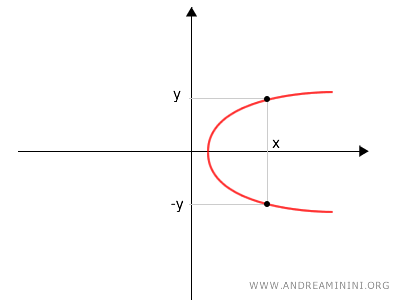
Note: It is important to note that the equation $ x=ay^2+by+c $ is not a function, as for each x value, there are two corresponding y values, except at the vertex of the parabola. Therefore, it cannot be considered a function from x to y.

How to Find the Equation of a Parabola

To determine the equation of a parabola, you need specific information, which can vary depending on the form of the equation you're using.

The most common forms of a parabola's equation are:

• Vertical Parabola
  The axis of symmetry is parallel to the y-axis: $$ y = ax^2 + bx + c $$
• Horizontal Parabola
  The axis of symmetry is parallel to the x-axis: $$ x = ay^2 + by + c $$

Generally, to find the coefficients \(a\), \(b\), and \(c\) of a parabola's equation, you need at least three distinct parameters or specific combinations of points and geometric features (known as "conditions") such as the vertex, focus, and directrix.

Here are some conditions necessary to fully determine the equation of a parabola:

• Three Distinct Points
  If you know the coordinates of three distinct points that the parabola passes through, you can find the coefficients \(a\), \(b\), and \(c\) by solving a system of linear equations.
• Vertex and Another Point
  If you know the coordinates of the vertex (\(h, k\)) and another point (\(x_1, y_1\)), you can find the equation of the parabola. The equation in this case is \(y = a(x-h)^2 + k\). You still need another point to determine \(a\).
• Axis of Symmetry and Two Points
  If you know the axis of symmetry, which gives you the value \(x = h\), and the coordinates of two distinct points that the parabola passes through, you can find the equation. The axis of symmetry helps determine the value of \(b\) if the equation is in the form \(y = ax^2 + bx + c\).
• Directrix and Focus
  If you know the coordinates of the focus (\(h, k + p\)) and the directrix \(y = k - p\) for a vertical parabola, you can find the equation in the form \( (x - h)^2 = 4p(y - k) \). Similarly, for a horizontal parabola, knowing the focus and directrix determines the equation in the form \( (y - k)^2 = 4p(x - h) \).

And so on