Pencil of Parabolas
A pencil of parabolas (or bundle of parabolas) is the linear combination of two base parabolas, known as the generating parabolas of the pencil.
For example, given a generating parabola with \( a_1 \ne 0 \) in implicit form:
$$ y + a_1 x^2 + b_1 x + c_1 = 0 $$
and a second generating parabola with \( a_2 \ne 0 \):
$$ y + a_2 x^2 + b_2 x + c_2 = 0 $$
a pencil of parabolas can be described as:
$$ (y + a_1 x^2 + b_1 x + c_1) + \lambda \cdot (y + a_2 x^2 + b_2 x + c_2) = 0 $$
where \(\lambda \in \mathbb{R} \) is a real parameter.
By varying \(\lambda\), you obtain all the parabolas in the pencil.
The parabolas in a pencil can intersect at one, none, or two points on the plane, called the base points of the pencil.
Note: In other words, a pencil of parabolas is a family of parabolas that depend on a variable parameter, and the specific form of the pencil depends on how the coefficients of the quadratic equation defining the parabolas vary. With \(\lambda = 0\), you get the first parabola. $$ (y + a_1 x^2 + b_1 x + c_1) + 0 \cdot (y + a_2 x^2 + b_2 x + c_2) = 0 $$ $$ y + a_1 x^2 + b_1 x + c_1 = 0 $$ However, no value of \(\lambda\) can represent the second parabola. Therefore, the previous linear combination represents all combinations of the two parabolas except one (the second parabola). To represent the second parabola as well, you would need to write the pencil of parabolas using two real parameters instead of one: $$ \lambda_1 \cdot (y + a_1 x^2 + b_1 x + c_1) + \lambda_2 \cdot (y + a_2 x^2 + b_2 x + c_2) = 0 $$ where \( \lambda_1, \lambda_2 \in \mathbb{R} \).
Alternatively, the pencil of parabolas can also be represented in this general equivalent form:
$$ (a_1 + \lambda a_2 ) x^2 + (b_1 + \lambda b_2) x + (1 + \lambda) y + c_1 + \lambda c_2 = 0 $$
This form is very useful because it can be written as:
$$ A x^2 + B x + C y + D = 0 $$
where in our case:
$$ A = a_1 + \lambda a_2 $$
$$ B = b_1 + \lambda b_2 $$
$$ C = 1 + \lambda $$
$$ D = c_1 + \lambda c_2 $$
This allows us to find the equations for the vertex and focus using the formulas for any parabola.
- Focus
$$ F \begin{pmatrix} - \frac{B}{2A}, \frac{1 - \Delta}{4A} \end{pmatrix} $$ - Vertex
$$ V \begin{pmatrix} - \frac{B}{2A}, - \frac{\Delta}{4A} \end{pmatrix} $$ - Directrix
$$ y = - \frac{1 + \Delta}{4A} $$ - Axis of Symmetry
$$ x = - \frac{B}{2A} $$
Where A, B, C are the coefficients of the equation of the pencil of parabolas \( y = Ax^2 + Bx + C \) and the discriminant is \( \Delta = B^2 - 4AC \).
Note: For it to be a pencil of lines, the quadratic component must always be present as in any parabola. In other words, the coefficient A must be non-zero (\( A \ne 0 \)).
A Practical Example
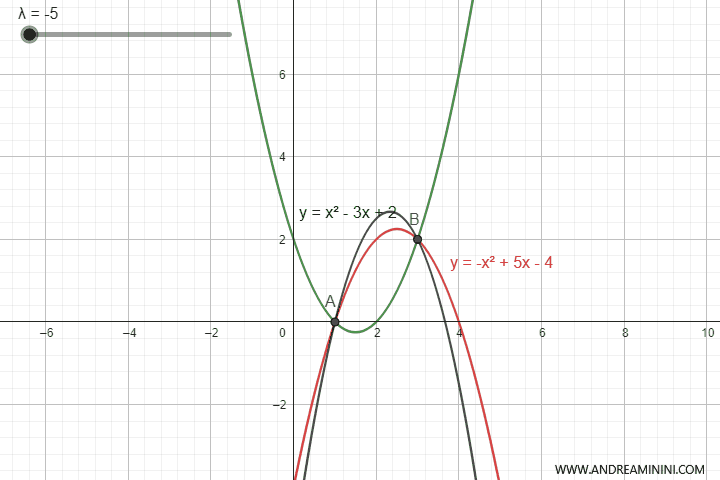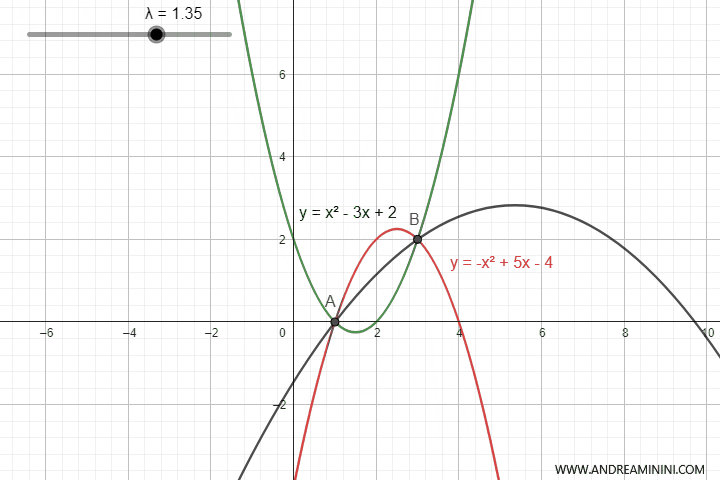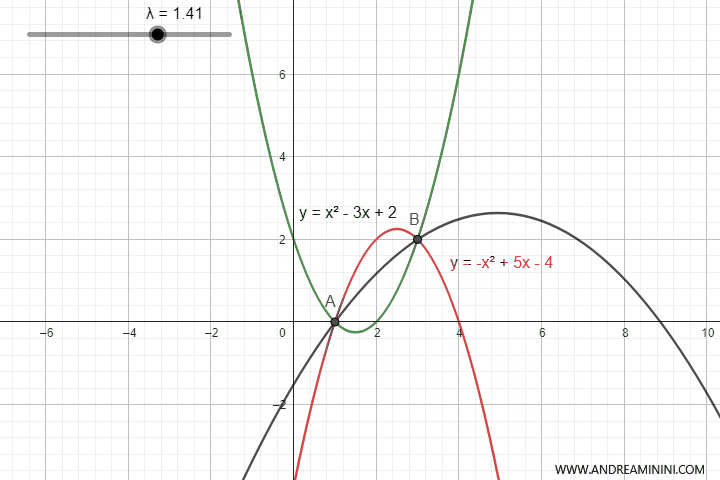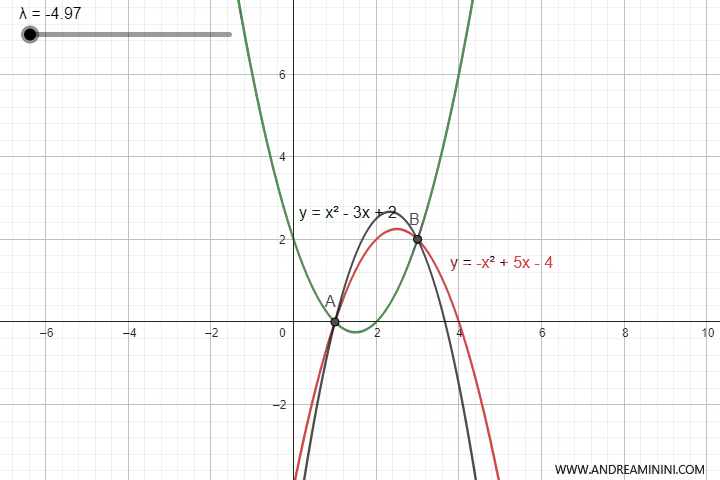
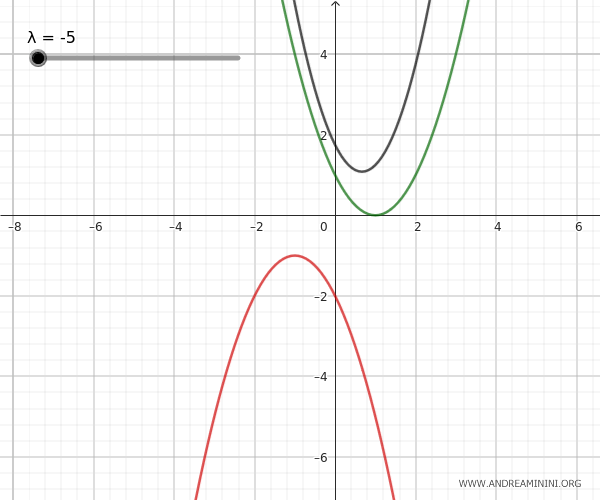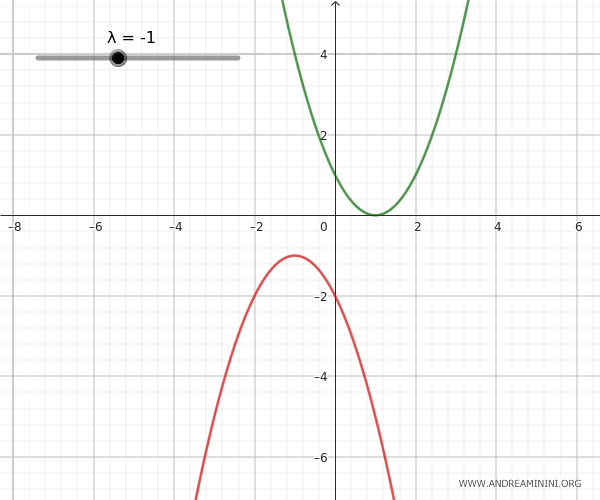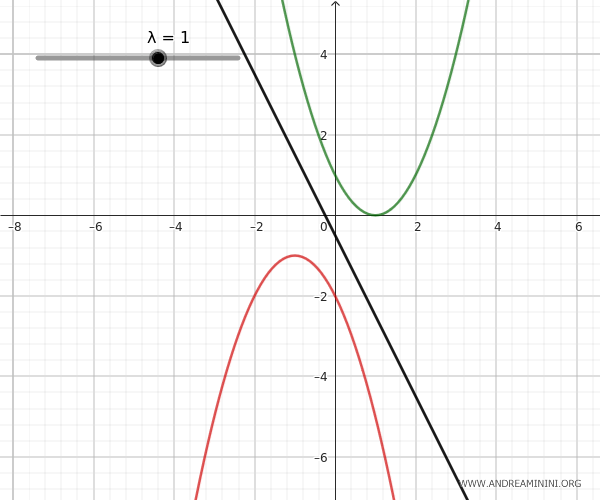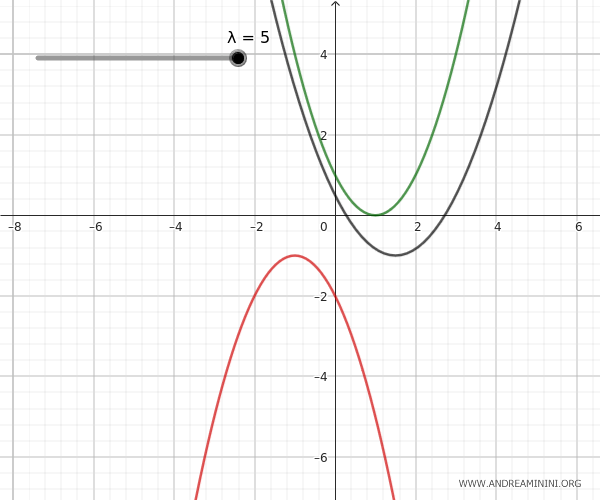
Let's consider two generating parabolas:
$$ p_1: y = x^2 - 3x + 2 $$
$$ p_2: y = -x^2 + 5x - 4 $$
Write both parabolas in implicit form:
$$ p_1: y - x^2 + 3x - 2 = 0 $$
$$ p_2: y + x^2 - 5x + 4 = 0 $$
In this case, the two generating parabolas intersect at two points, A(1,0) and B(3,2).
These two points are also the base points of the pencil of parabolas.
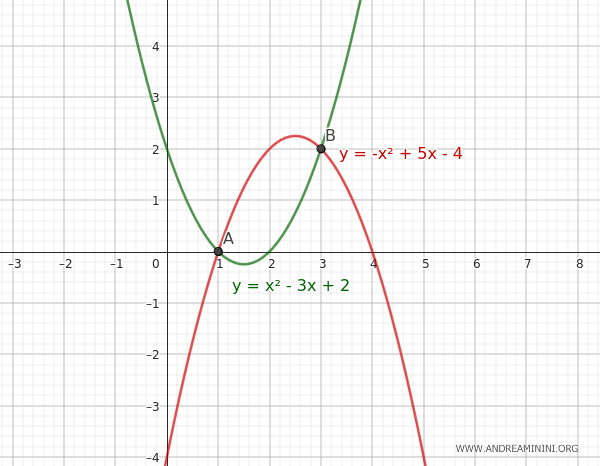
The pencil of parabolas obtained from the linear combination of the two generating parabolas is:
$$ p_1 + \lambda \cdot p_2 = 0 $$
$$ (y - x^2 + 3x - 2) + \lambda \cdot (y + x^2 - 5x + 4) = 0 $$
$$ (\lambda - 1) x^2 + (3 - 5\lambda) x + (1 + \lambda) y - 2 + 4\lambda = 0 $$
By varying the parameter \(\lambda\), we obtain all the parabolas of the pencil that pass through the intersection points of the parabolas.
To get the equation of the pencil of parabolas, I could have taken any pair of parabolas from the pencil, even degenerate parabolas which, at certain values of the parameter \(\lambda\), turn into lines.
Example: To find the equations of the pencil of parabolas, I can also use the degenerate parabolas of the pencil. For example, to find the equation of the pencil formed by two intersecting parabolas with base points A(1,0) and B(3,2). When the generators intersect, two parabolas degenerate into two lines. One parabola degenerates into a line that passes through both base points A and B, while another parabola degenerates into two lines parallel to the axis of symmetry, each passing through one base point.
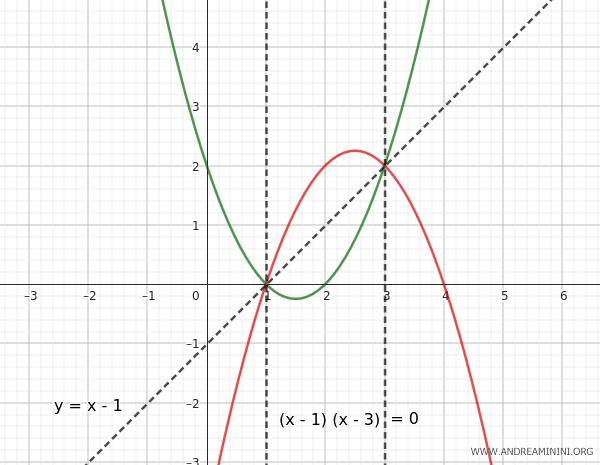
To find the pencil of parabolas, I consider the degenerate parabolas. The equation of the line passing through both points A(x1, y1) = (1,0) and B(x2, y2) = (3,2) is as follows:
$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$
$$ \frac{y - 0}{2 - 0} = \frac{x - 1}{3 - 1} $$
$$ \frac{y}{2} = \frac{x - 1}{2} $$
$$ y = x - 1 $$
$$ y - x + 1 = 0 $$
The second parabola has roots at 1 and 3, so it is the product of the lines \((x - 1)\) and \((x - 3 )\).
$$ (x - 1)(x - 3) = 0 $$
Thus, the equation of the pencil of parabolas is the linear combination of the two degenerate parabolas:
$$ y - x + 1 + \lambda [(x - 1)(x - 3)] = 0 $$
The final result is always the same.Types of Generating Parabolas
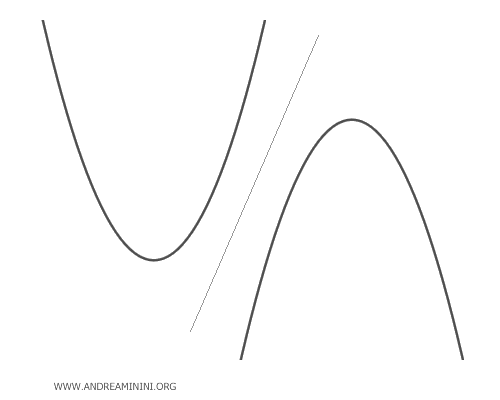
The pencil of parabolas can be generated by intersecting, tangent, external, or congruent parabolas with or without a common point. For simplicity, I will only consider the case of vertical parabolas, i.e., parallel to the y-axis.
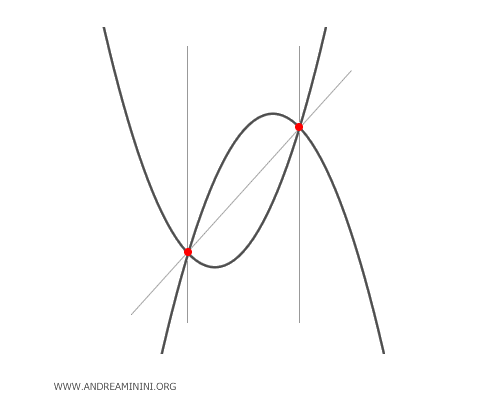
- Intersecting Parabolas
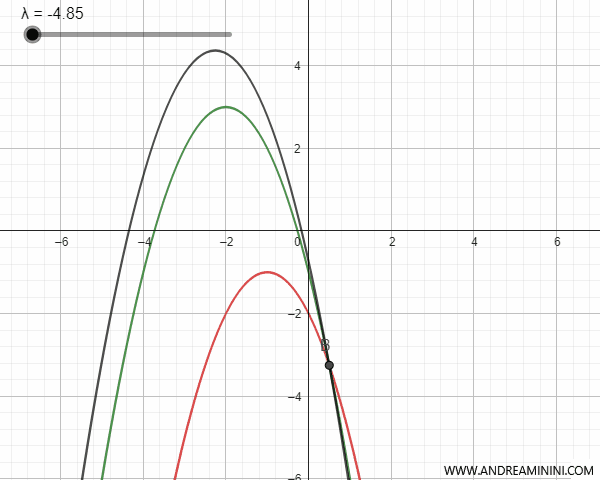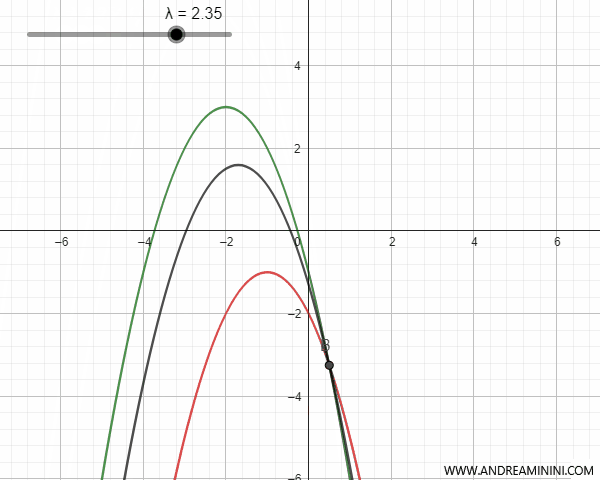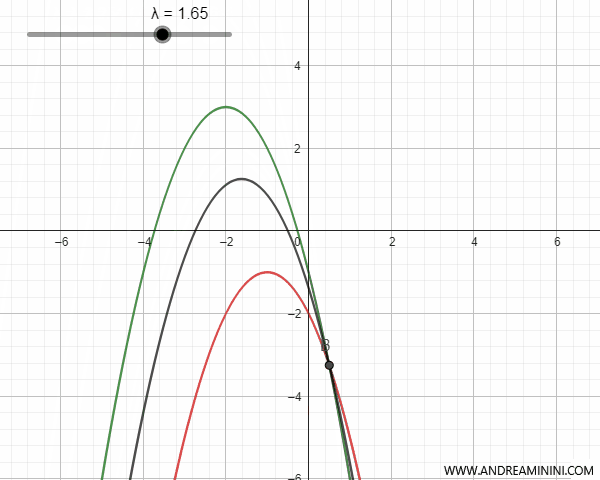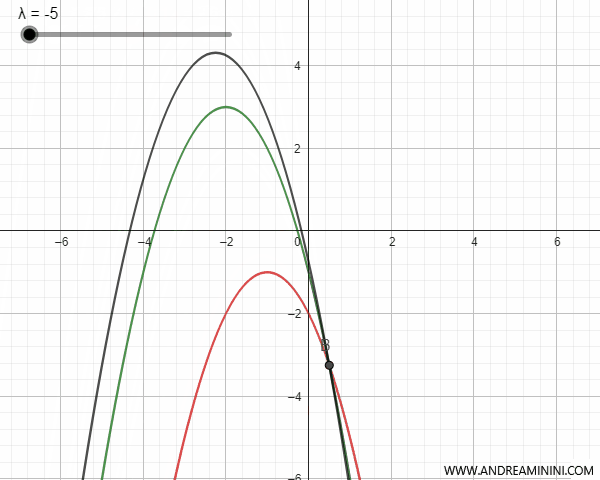
Intersecting parabolas have two intersection points that coincide with the two base points of the pencil of parabolas. For certain values of the parameter \(\lambda\), the parabola of the pencil degenerates into a line passing through the base points and is called a "degenerate parabola."
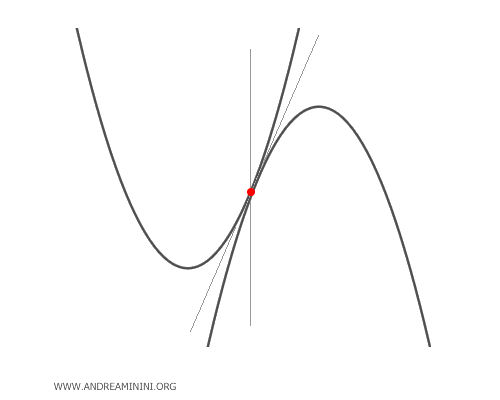
- Tangent Parabolas
Tangent parabolas have a single intersection point that coincides with the only base point of the pencil. For certain values of the parameter \(\lambda\), the parabola of the pencil degenerates into a line passing through the base point. Specifically, it degenerates into a tangent line and a line parallel to the axis of symmetry.
- External Parabolas
External parabolas do not have any common points, so there are no base points for the pencil. For a particular value of the parameter \(\lambda\), the generated parabola can degenerate into a line situated between the two parabolas.
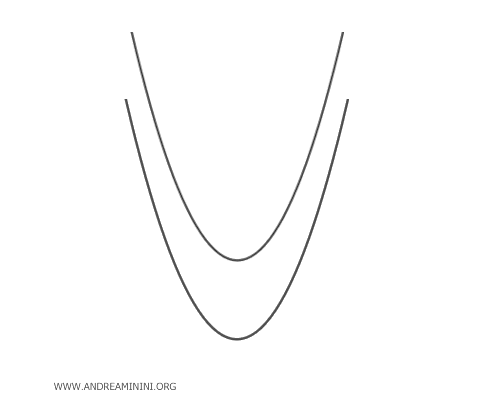
- Congruent Parabolas
Congruent parabolas do not have any common points if they share the same axis of symmetry and do not degenerate into a line.
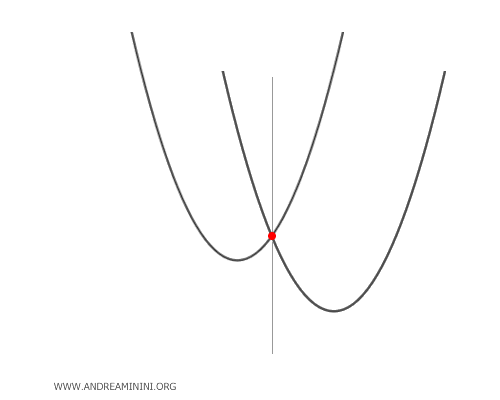
Conversely, if the generating parabolas are congruent and have parallel but non-coincident axes of symmetry, they intersect at a base point. In this latter case, for some values of \(\lambda\), the generated parabola can degenerate into a line parallel to the axis of symmetry that passes through the base point.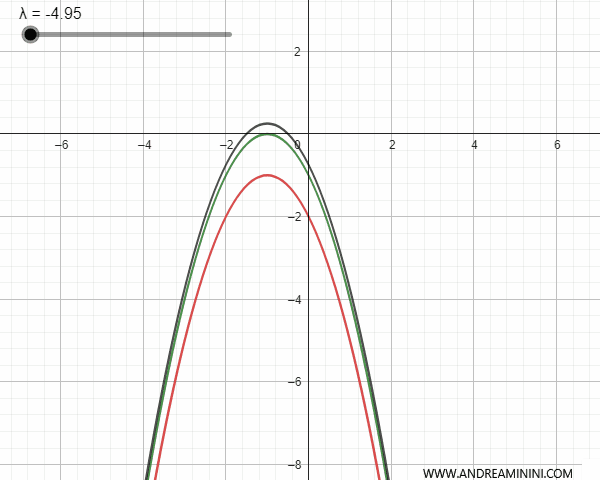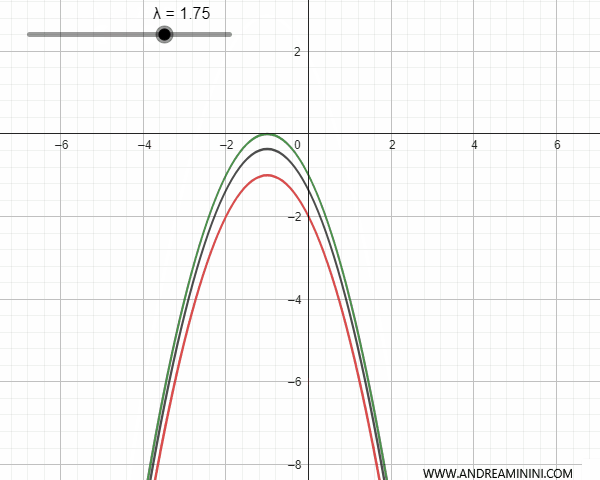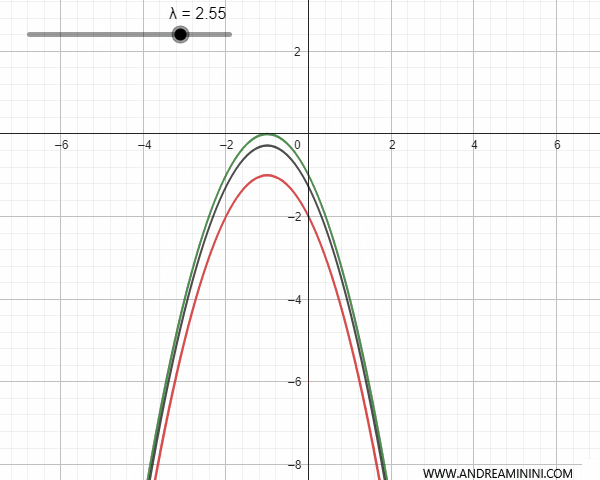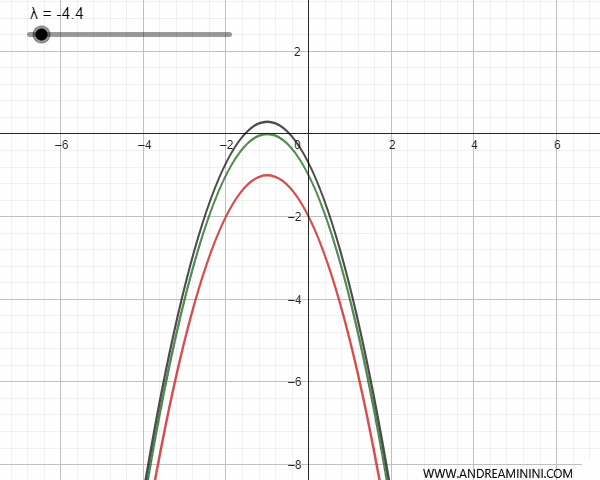
How to Find the Equations of the Generating Parabolas of the Pencil
To find the equations of the generating parabolas of the pencil, collect the terms with respect to the parameter \(\lambda\).
The first generating parabola is obtained by setting \(\lambda = 0\).
The second generating parabola is obtained by setting the expression multiplied by \(\lambda\) to zero.
Example
Consider the equation of this pencil of parabolas:
$$ (\lambda - 1) x^2 + (3 - 5\lambda) x + (1 + \lambda) y - 2 + 4\lambda = 0 $$
Collect the terms with respect to the parameter \(\lambda\):
$$ (\lambda - 1) x^2 - 5\lambda x + 3x + \lambda y + y + 4\lambda - 2 = 0 $$
$$ \lambda (x^2 - 5x + y + 4) - x^2 + 3x + y - 2 = 0 $$
The first generating parabola is found by setting \(\lambda = 0\):
$$ 0 \cdot (x^2 - 5x + y + 4) - x^2 + 3x + y - 2 = 0 $$
$$ -x^2 + 3x + y - 2 = 0 $$
So, the first generator is \( y = x^2 - 3x + 2 \).
The second generator is obtained by setting the term multiplied by \(\lambda\) to zero:
$$ x^2 - 5x + y + 4 = 0 $$
So, the second generator is \( y = -x^2 + 5x - 4 \).
Thus, I have found both generating parabolas of the pencil.
How to Find the Base Points of the Pencil of Parabolas
To find the potential base points of the pencil of parabolas, I need to solve the system of equations for the two generators.
- If the system has two solutions, there are two base points and the generators intersect.
- If the system has one solution, there is one base point, and the generators are either tangent or congruent with different axes of symmetry. Therefore, it is also necessary to verify if the tangency condition is met.
- If the system has no solutions, there are no base points. In this case, the parabolas could be external or congruent with the same axis of symmetry.
Example
The equations of the two generating parabolas of the pencil are:
$$ y = x^2 - 3x + 2 $$
$$ y = -x^2 + 5x - 4 $$
Solving this system of equations to find the intersection points:
$$ \begin{cases} y = x^2 - 3x + 2 \\ y = -x^2 + 5x - 4 \end{cases} $$
In this case, I can set \( y = x^2 - 3x + 2 \) equal to \( y = -x^2 + 5x - 4 \) because they are both equal to \( y \):
$$ x^2 - 3x + 2 = -x^2 + 5x - 4 $$
Move all terms to the same side of the equation:
$$ x^2 + x^2 - 3x - 5x + 2 + 4 = 0 $$
$$ 2x^2 - 8x + 6 = 0 $$
Divide everything by 2 to simplify:
$$ x^2 - 4x + 3 = 0 $$
This is a quadratic equation that can be solved using the quadratic formula:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Where \( a = 1 \), \( b = -4 \), and \( c = 3 \):
$$ x = \frac{4 \pm \sqrt{16 - 12}}{2} $$
$$ x = \frac{4 \pm \sqrt{4}}{2} $$
$$ x = \frac{4 \pm 2}{2} $$
So, the solutions are:
$$ x = \frac{4 + 2}{2} = 3 $$
$$ x = \frac{4 - 2}{2} = 1 $$
Now, I calculate the values of \( y \) for the values of \( x \) found:
- For \( x = 1 \), then \( y = (1)^2 - 3(1) + 2 = 1 - 3 + 2 = 0 \)
- For \( x = 3 \), then \( y = (3)^2 - 3(3) + 2 = 9 - 9 + 2 = 2 \)
Thus, the base points of the pencil are \( (1, 0) \) and \( (3, 2) \).
Since there are two distinct base points, the parabolas intersect at two points, making them intersecting parabolas.
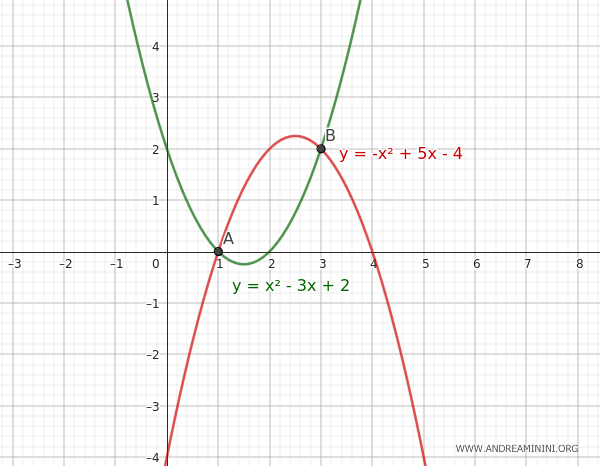
And so on.
