Degenerate Parabolas

A parabola within a family is termed a "degenerate parabola" when, for a specific value of the parameter λ, it transforms into a straight line.

In a family of parabolas, a particular value of the parameter λ removes either the variable y or the quadratic term x² from the equation.

In these cases, the parabola "degenerates" into a line or a pair of lines.

A Practical Example

Consider the family of parabolas

$$ (y-x^2+3x-2) + \lambda \cdot (y+x^2-5x+4) = 0 $$

This equation generates an infinite number of parabolas opening upwards or downwards depending on the value of the parameter $ \lambda $.

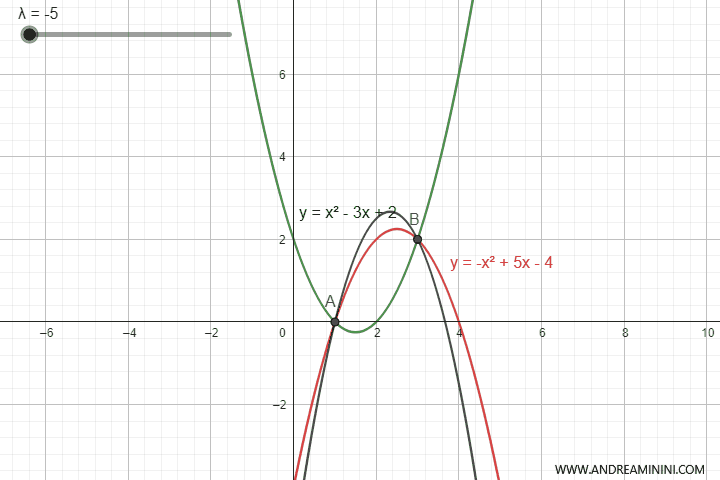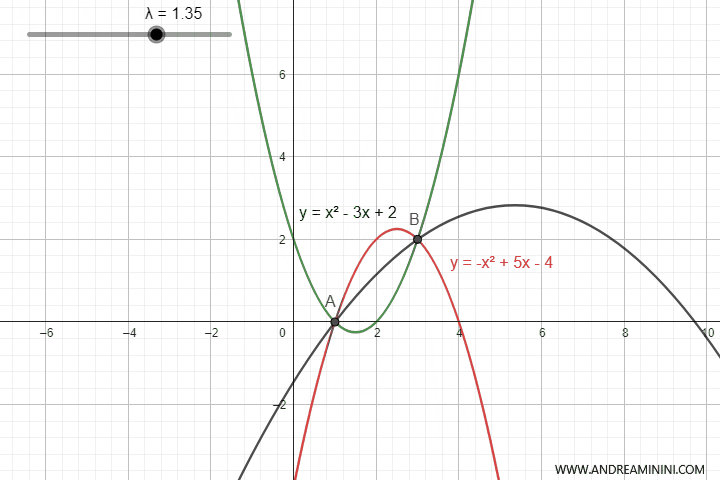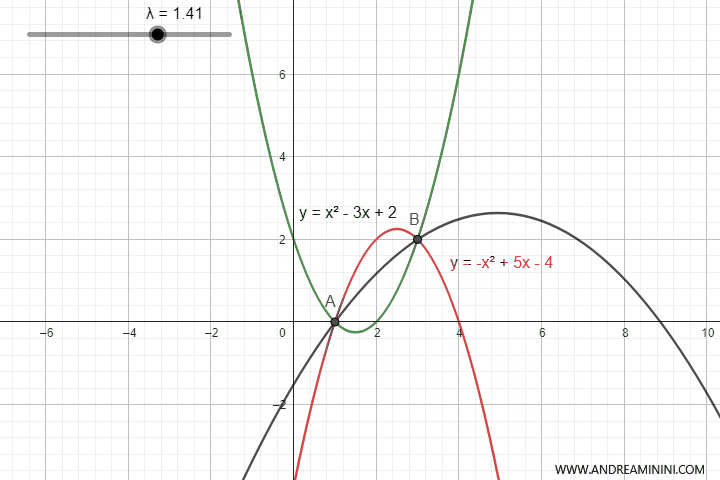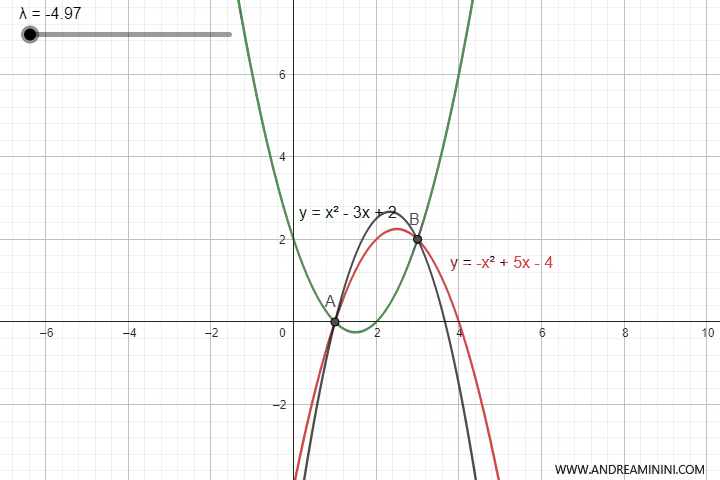
However, for certain values of $ \lambda $, the parabola degenerates into a straight line.

1] First Case

For instance, the value λ=-1 eliminates the variable y from the parabola's equation.

$$ (y-x^2+3x-2) + (-1) \cdot (y+x^2-5x+4) = 0 $$

$$ \require{cancel} \cancel{y}-x^2+3x-2 \cancel{-y}-x^2+5x-4 = 0 $$

$$ -2x^2+8x-6 = 0 $$

$$ -x^2+4x-3 = 0 $$

This quadratic equation has two solutions:

$$ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$

$$ x = \frac{-4 \pm \sqrt{4^2-4(-1)(-3)}}{2(-1)} $$

$$ x = \frac{-4 \pm \sqrt{16-12}}{-2} $$

$$ x = \frac{-4 \pm \sqrt{4}}{-2} $$

$$ x = \frac{-4 \pm 2}{-2} $$

$$ x = 2 \pm 1 = \begin{cases} x= 3 \\ \\ x=1 \end{cases} $$

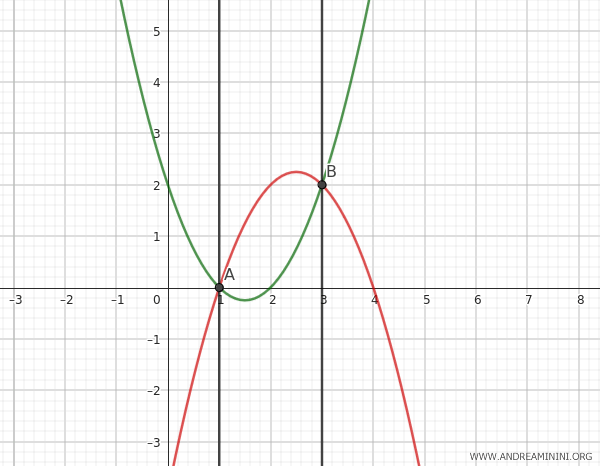
Therefore, I can express the equation $ -x^2+4x-3 = 0 $ as the product of two lines:

$$ (x-3) \cdot (x-1) = 0 $$

In other words, the parabola degenerates into two intersecting lines passing through the base points A and B.

2] Second Case

Another instance of a degenerate parabola occurs when the parameter is λ=1, as it removes the quadratic component x² from the equation.

$$ (y-x^2+3x-2) + (1) \cdot (y+x^2-5x+4) = 0 $$

$$ y\cancel{-x^2}+3x-2+ y+\cancel{x^2}-5x+4 = 0 $$

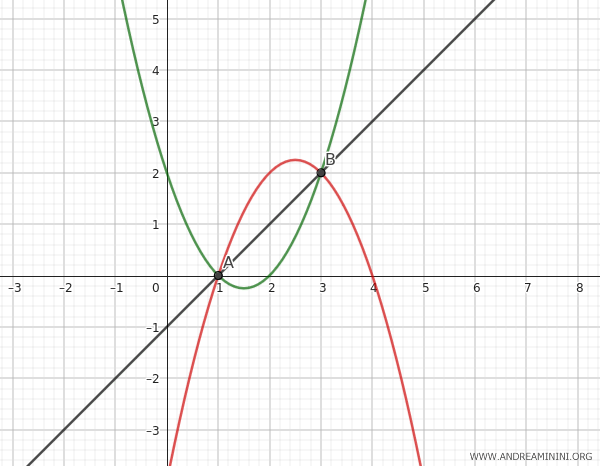
$$ 2y-2x+2= 0 $$

In this case, the parabola within the family degenerates into a line passing through the base points A and B.

And so on.