Bundle of Parabolas Passing Through Two Points

A bundle of parabolas that pass through two distinct points \( A(x_A, y_A) \) and \( B(x_B, y_B) \) can be described by the equation $$ y = mx + q + \lambda (x - x_A)(x - x_B) $$ where \( y = mx + q \) is the line passing through the points and \( \lambda \) is the parameter that generates the parabolas in the bundle.

The line passing through points A and B is given by the equation \( y = mx + q \), where \( m \) is the slope and \( q \) is the y-intercept.

You can find \( m \) and \( q \) using the coordinates of points A and B:

$$ m = \frac{y_B - y_A}{x_B - x_A} $$

$$ q = y_A - m x_A $$

By substituting the coordinates of A and B into the equation, it holds true for any value of \( \lambda \).

The proof that this equation represents a bundle of parabolas is based on the fact that for each value of \( \lambda \), the equation satisfies the coordinates of A and B, forming a curve that varies with \( \lambda \).

Example

Consider the points \( A(1, 0) \) and \( B(3, 2) \).

We need to find the equation of the bundle of parabolas passing through A and B.

The line passing through both points is:

$$ y = mx + q $$

First, calculate the slope of the line:

$$ m = \frac{y_B - y_A}{x_B - x_A} $$

$$ m = \frac{2 - 0}{3 - 1} = \frac{2}{2} $$

$$ m = 1 $$

Next, find the y-intercept:

$$ q = y_A - mx_A $$

$$ q = 0 - 1 \cdot 1 $$

$$ q = -1 $$

So, the equation of the line passing through A and B is:

$$ y = x - 1 $$

The equation of the bundle of parabolas is:

$$ y = mx + q + \lambda (x - x_A)(x - x_B) $$

$$ y = x - 1 + \lambda (x - 1)(x - 3) $$

This equation represents a set of parabolas that pass through points A and B, with their shapes changing based on the parameter \( \lambda \). Each parabola in the bundle is unique for a given value of \( \lambda \).

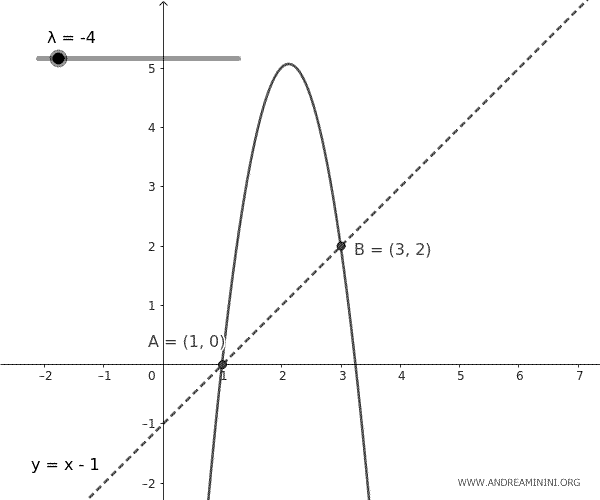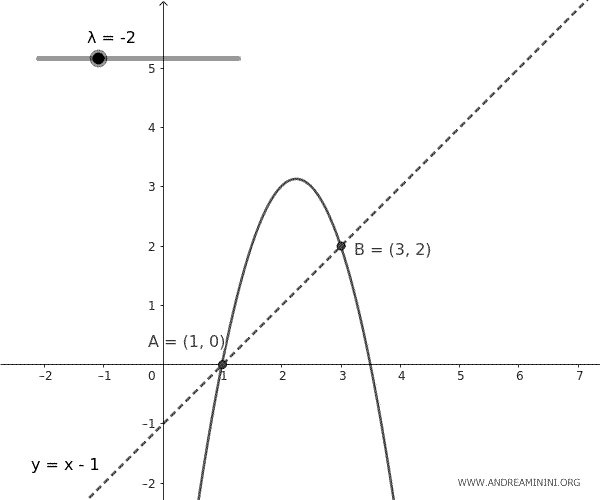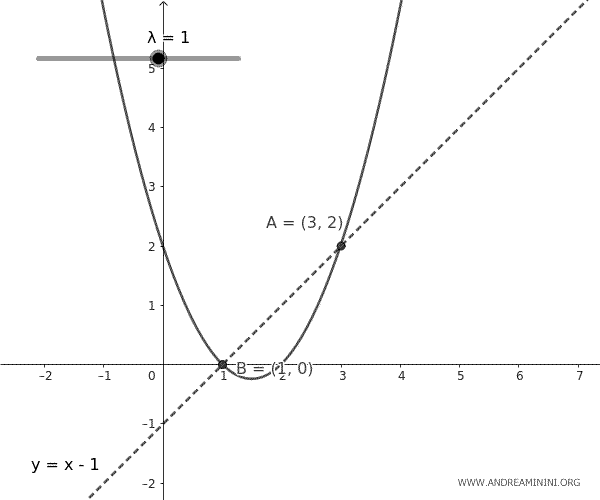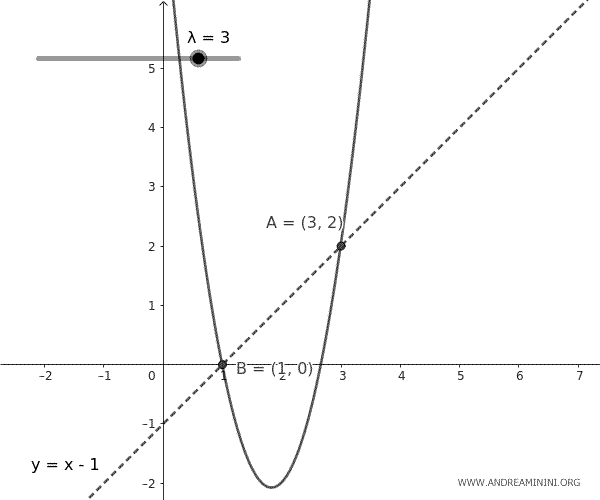
And so on.