A Pencil of Parabolas Tangent to a Line

A pencil of parabolas tangent at the point $ T(x_T;y_T) $ to the line $ r $ with the equation $ y = mx + q $ can be represented by the equation $$ y = mx + q + k (x - x_T)^2 $$

A Practical Example
The Proof

A Practical Example

Let's consider a line $ r $ with the equation

$$ y = -x + 2 $$

Now, take a point $ T $ on this line, $ T(1, 1) $.

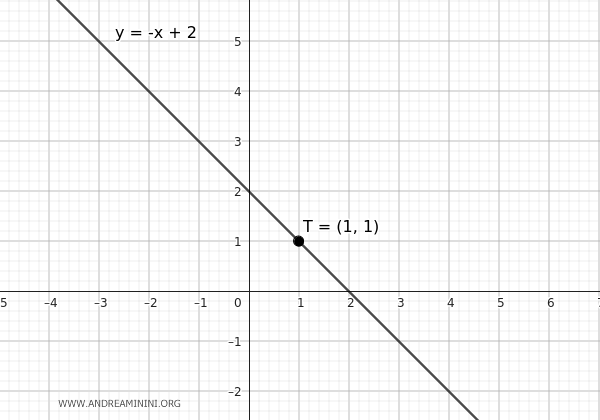
an example of a point on a line

The equation for the pencil of parabolas tangent to the line $ r $ at the point $ T $ is:

$$ y = mx + q + k (x - x_T)^2 $$

$$ y = -x + 2 + k (x - 1)^2 $$

Let's construct some parabolas from this pencil using different values of $ k $:

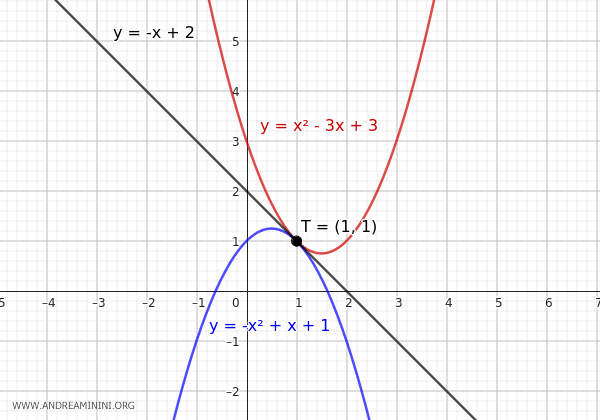
For example, for $ k=1 $ we get the equation

$$ y = -x + 2 + 1 \cdot (x - 1)^2 $$

$$ y = -x + 2 + x^2-2x+1 $$

$$ y = x^2-3x + 3 $$

Here is the graph of the parabola, which is indeed tangent to the line at point T.

a parabola from the pencil

Let's take another example with $ k = -1 $

$$ y = -x + 2 - 1 \cdot (x - 1)^2 $$

$$ y = -x + 2 - x^2 + 2x - 1 $$

$$ y = -x^2 + x + 1 $$

The graph of this parabola is also tangent to the line at point T.

another parabola from the pencil tangent at point T to the line r

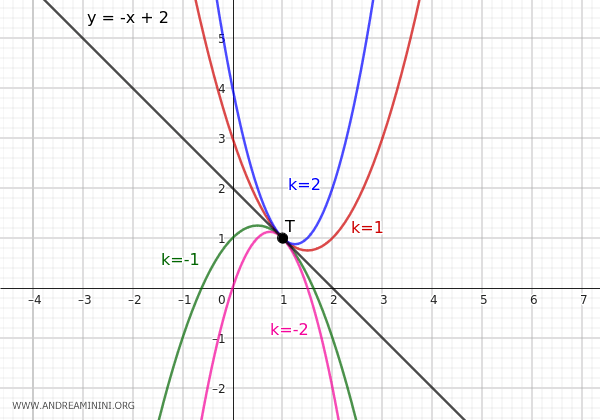
In a similar way, we can obtain all the other infinite parabolas in the pencil.

For $ k = 1 $ we have the equation $ y = x^2 - 3x + 3 $
For $ k = -1 $ we have the equation $ y = -x^2 + x + 1 $
For $ k = 2 $ we have the equation $ y = 2x^2 - 5x + 4 $

All these parabolas are tangent to the line $ y = -x + 2 $ at the point $ T(1, 1) $.

tangent parabolas

The Proof

To prove that the equation $ y = mx + q + k (x - x_T)^2 $ represents a pencil of parabolas tangent to the line, consider a point $ T(x_T, y_T) $ on the line $ r $:

$$ y = mx + q $$

Since $ T $ lies on the line $ r $, this equation holds true:

$$ y_T = mx_T + q $$

Now consider the equation:

$$ y = mx + q + k (x - x_T)^2 $$

To ensure that all parabolas in the pencil are tangent to the line $ r $ at $ T $, we must verify that the derivative of the parabola at $ T $ equals the slope of the line $ r $, which is $ m $.

Calculate the first derivative of $ y $ with respect to $ x $:

$$ \frac{dy}{dx} = m + 2k(x - x_T) $$

Evaluate the derivative at the point $ T(x_T, y_T) $:

$$ \left. \frac{dy}{dx} \right|_{x = x_T} = m + 2k(x_T - x_T) = m $$

The first derivative of the parabola at point $ T $ equals the slope $ m $ of the line $ r $. This means the line is tangent to the parabola at point $ T $.

Next, let's verify that the point $ T $ lies on the parabola.

Substitute $ x_T $ and $ y_T $ into the equation of the parabola:

$$ y_T = mx_T + q + k(x_T - x_T)^2 = mx_T + q $$

This holds true since $ y_T = mx_T + q $, so the point $ T $ also lies on the parabola.

In conclusion, we have demonstrated that the equation $ y = mx + q + k (x - x_T)^2 $ represents a pencil of parabolas all tangent to the line $ r: y = mx + q $ at the point $ T(x_T, y_T) $.

And so on.