How to Determine the Equation of a Parabola Given a Point and the Focus

To find the equation of a parabola given a point \((x_0, y_0)\) on the parabola and the focus \((x_F, y_F)\), you need additional information to infer the parabola's orientation (e.g., vertical, horizontal, opening up or down, to the right or left, etc.). Usually, this extra information is provided in the problem statement.

In general, you can work with multiple hypotheses simultaneously.

• Vertical Parabola
  The axis of symmetry is vertical, and the directrix is horizontal. It can open upwards or downwards.
• Horizontal Parabola
  The axis of symmetry is horizontal, and the directrix is vertical. It can open to the right or left.

Practical Example

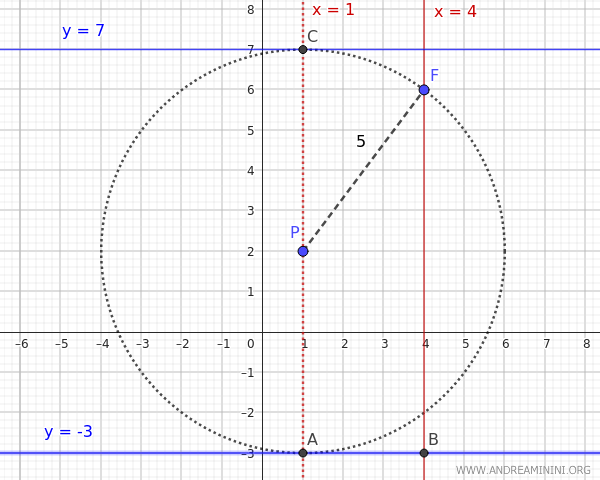
Let's consider a point \((1, 2)\) and the focus \((4, 6)\).

Now, we need to determine whether the parabola has a vertical or horizontal axis of symmetry.

Knowing only a point and the focus does not allow us to determine the parabola's orientation. Therefore, if the problem does not provide further information, we consider both possibilities.

1] Parabola with a Vertical Axis of Symmetry

We know the coordinates of a point \(P((x_0,y_0)=(1, 2))\) on the parabola and the focus \((x_F,y_F)=(4, 6)\). Assuming the parabola has a vertical axis of symmetry:

The focus and the vertex are both on the axis of symmetry, so if the axis is vertical, they share the same x-coordinate \( (h, k) = (4,k) \). Hence, \( h = 4 \).

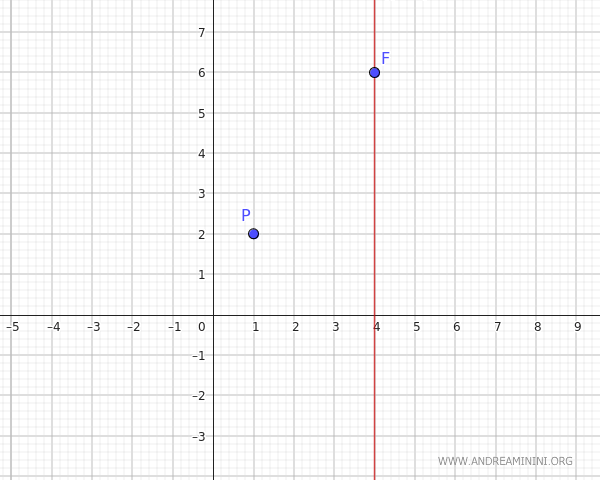
The general equation of a parabola with a vertical axis of symmetry is:

$$ (x - h)^2 = 4p(y - k) $$

Where \((h, k)\) is the vertex and \(p\) is the distance between the vertex and the focus.

Knowing that the axis of symmetry is vertical and the vertex is \( (h, k) = (4,k) \), we have:

$$ (x - 4)^2 = 4p(y - k) $$

In a parabola, the distance between a point \(P\) and the focus is equal to the distance between the same point \(P\) and the directrix.

We calculate the distance between the point \( P(1,2) \) and the focus \((x_F,y_F)=(4, 6)\):

$$ d_1 = \sqrt{(x_0 - x_F)^2 + (y_0 - y_F)^2} $$

$$ d_1 = \sqrt{(1 - 4)^2 + (2 - 6)^2} $$

$$ d_1 = \sqrt{(-3)^2 + (-4)^2} $$

$$ d_1 = \sqrt{9 + 16} $$

$$ d_1 = \sqrt{25} $$

$$ d_1 = 5 $$

The distance between point \(P\) and the focus \(F\) is 5.

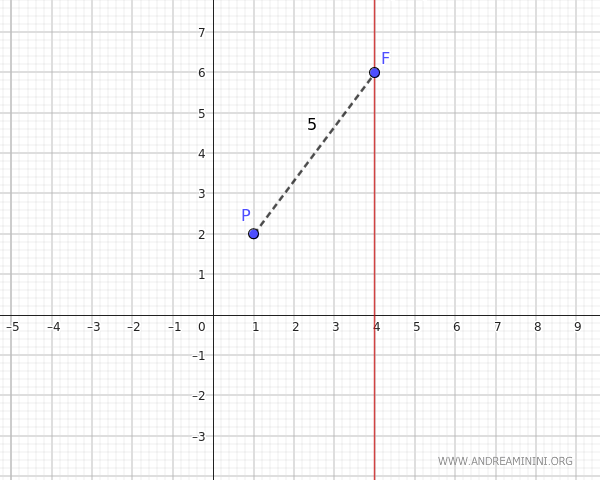
Since the parabola's axis of symmetry is vertical and passes through the focus \( (4,6) \), the axis has the same x-coordinate as the focus:

$$ x = x_F $$

$$ x = 4 $$

The line parallel to the axis of symmetry \( x = 4 \) that passes through the point \( P(1,2) \) has the same x-coordinate as the point, which is \( x_p=1 \).

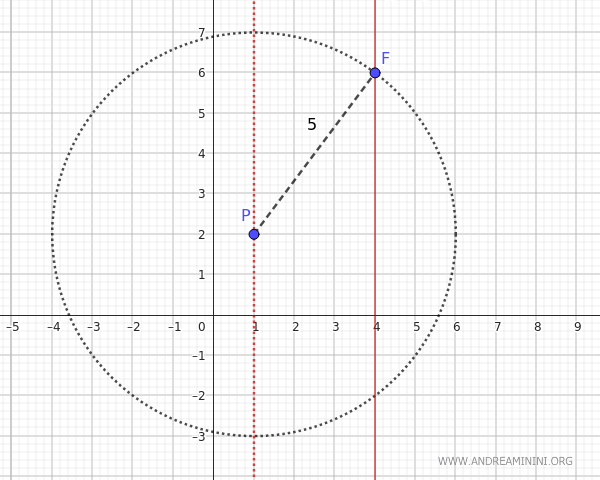
To find the directrix, we find the points of intersection between the line \( x_P=1 \) and a circle centered at \( P(1,2) \) with a radius \( d_1 = 5 \).

$$ \begin{cases} x = x_P \\ \\ (x-x_P)^2 + (y-y_P)^2 = d_1^2 \end{cases} $$

$$ \begin{cases} x = x_P \\ \\ (x-1)^2 + (y-2)^2 = 5^2 \end{cases} $$

$$ \begin{cases} x = x_P \\ \\ (1-1)^2 + (y-2)^2 = 25 \end{cases} $$

$$ \begin{cases} x = x_P \\ \\ (y-2)^2 = 25 \end{cases} $$

$$ \begin{cases} x = x_P \\ \\ y^2-4y+4 = 25 \end{cases} $$

$$ \begin{cases} x = x_P \\ \\ y^2-4y-21 = 0 \end{cases} $$

The quadratic equation has two solutions:

$$ y = \frac{-b \pm \sqrt{b^2-4ac} }{2a} $$

$$ y = \frac{-(-4) \pm \sqrt{(-4)^2-4 \cdot 1 \cdot (-21)} }{2 \cdot 1} $$

$$ y = \frac{4 \pm \sqrt{16+84} }{2} $$

$$ y = \frac{4 \pm \sqrt{100} }{2} $$

$$ y = \frac{4 \pm 10 }{2} $$

$$ y = 2 \pm 5 = \begin{cases} y= 2+5 = 7\\ \\ y = 2-5 = -3 \end{cases} $$

So, the directrix of the parabola can be:

$$ y_D = 7 \text{ or } y_D = -3 $$

Let's analyze both hypotheses:

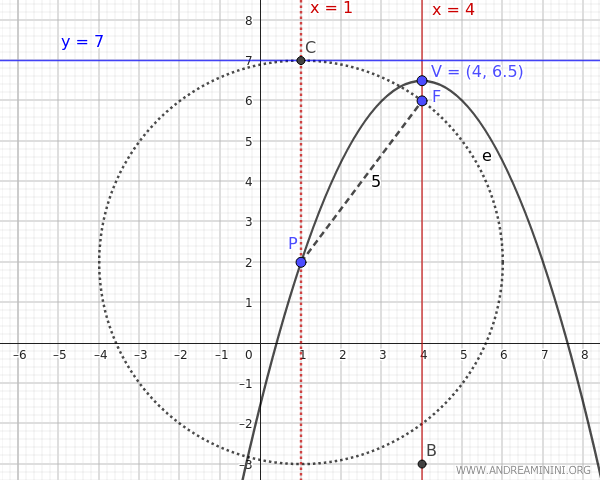
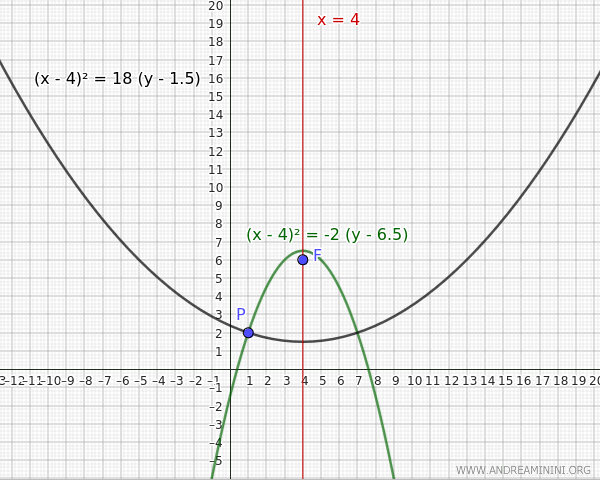
• If \( y_D = 7 \), the midpoint between the focus \( F (x_F,y_F)=(4,6) \) and the directrix \( y_D = 7 \) is the vertex of the parabola located at: $$ V(h,k) = (4, \frac{6+7}{2}) = (4, 6.5) $$ Thus, the distance between the focus and the vertex is: $$ p = y_F - k = 6- 6.5 = -0.5 $$ Hence, the equation of the parabola is: $$ (x - 4)^2 = 4p(y - k) $$ $$ (x - 4)^2 = 4 \cdot (-0.5) \cdot (y - 6.5) $$ $$ (x - 4)^2 = -2 (y - 6.5) $$
  
• If \( y_D = -3 \), the midpoint between the focus \( F (x_F,y_F)=(4,6) \) and the directrix \( y_D = - 3 \) is the vertex of the parabola located at: $$ V(h,k) = (4, \frac{6+(-3)}{2}) = (4,1.5) $$ Thus, the distance between the focus and the vertex is: $$ p = y_F - k = 6- 1.5 = 4.5 $$ Hence, the equation of the parabola is: $$ (x - 4)^2 = 4p(y - k) $$ $$ (x - 4)^2 = 4 \cdot 4.5 \cdot (y - 1.5) $$ $$ (x - 4)^2 = 18 (y - 1.5) $$
  

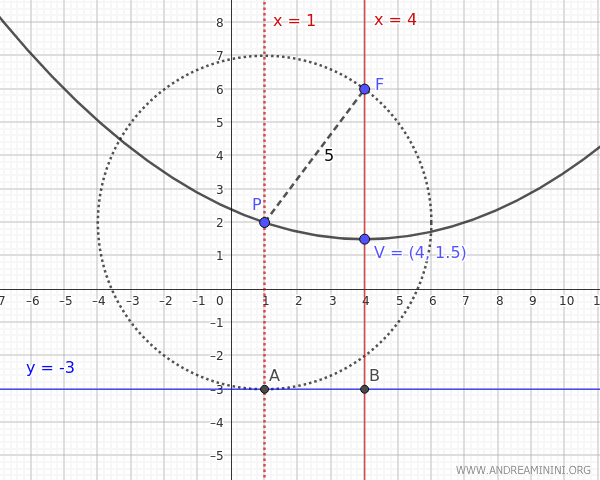
In the absence of further information, both hypotheses are possible: the parabola can open either upwards or downwards.

2] Parabola with a Horizontal Axis of Symmetry

The coordinates of the point are \( P(x_0,y_0)=(1, 2)\), and the coordinates of the focus of the parabola are \((x_F,y_F)=(4, 6)\). Given that the parabola has a horizontal axis of symmetry, we can proceed as follows:

The equation of a parabola with its axis of symmetry parallel to the x-axis is:

$$ (y-k)^2 = 4p(x-h) $$

Since the focus and the vertex lie on the axis of symmetry, and this axis is horizontal, they share the same y-coordinate: $ (h, k) = (h, 6) $. Therefore, $ k = 6 $.

$$ (y-6)^2 = 4p(x-h) $$

Given that the point \( P(x_0,y_0)=(1, 2)\) lies on the parabola, it must satisfy the equation.

So, we substitute x=1 and y=2 into the parabola's equation:

$$ (2-6)^2 = 4p(1-h) $$

$$ (-4)^2 = 4p(1-h) $$

$$ 16 = 4p(1-h) $$

The parameter p represents the distance between the focus and the vertex: $ p = x_F - h $ on the horizontal axis of symmetry, where $ x_F = 4 $.

$$ p = x_F - h = 4 - h $$

Substituting $ p $ with $ 4-h $ in the parabola's equation:

$$ 16 = 4 \cdot (4-h) \cdot (1-h) $$

$$ 16 = 4 \cdot (4 - 4h - h + h^2 ) $$

$$ 16 = 4 \cdot (4 - 5h + h^2 ) $$

$$ 16 = 16 - 20h + 4h^2 $$

$$ 4h^2 - 20h = 0 $$

$$ h \cdot (4h - 20) = 0 $$

This quadratic equation has two solutions: $ h = 0 $ and $ h = 5 $.

Therefore, we need to consider both cases:

• If $ h = 0 $, the distance between the focus and the vertex is $ p = 4-h = 4-0 = 4 $. Thus, the equation of the parabola with $ h = 0 $ and $ p = 4 $ is: $$ (y-6)^2 = 4p(x-h) $$ $$ (y-6)^2 = 4 \cdot 4 \cdot (x-0) $$ $$ (y-6)^2 = 16 (x-0) $$ Since $ p>0 $, the parabola opens to the right.
  
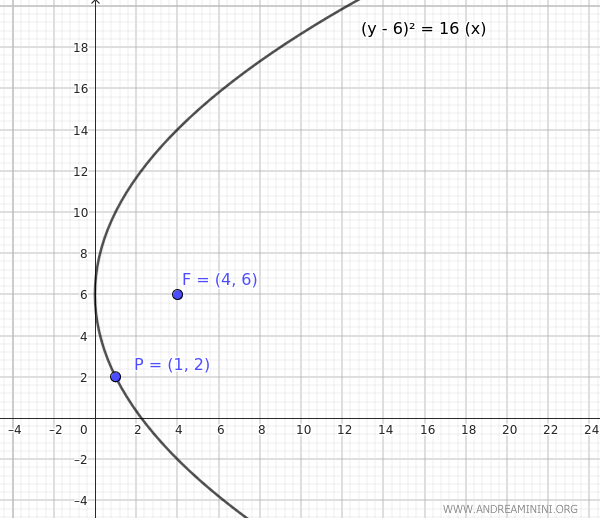
• If $ h = 5 $, the distance between the focus and the vertex is $ p = 4-h = 4-5 = -1 $. Thus, the equation of the parabola with $ h = 5 $ and $ p = -1 $ is: $$ (y-6)^2 = 4p(x-h) $$ $$ (y-6)^2 = 4 \cdot (-1) \cdot (x-5) $$ $$ (y-6)^2 = -4 (x-5) $$ Since $ p<0 $, the parabola opens to the left.
  

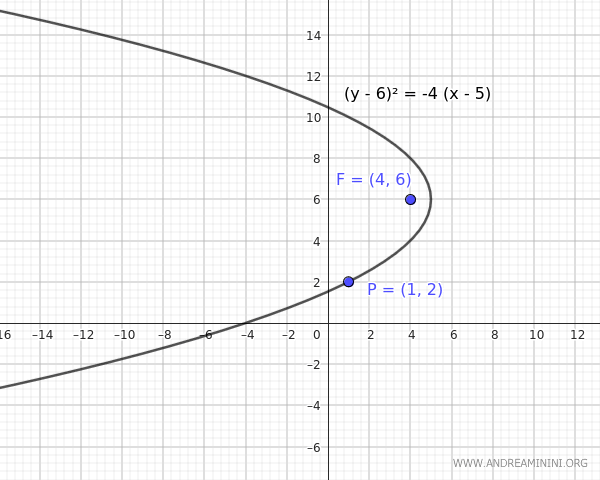
In the absence of additional information, both solutions are valid.

And so on.