Parabolic Segment

The parabolic segment is the region of the plane bounded by a parabolic arc and the chord that closes it.

Consider a secant line intersecting the parabola at points A and B.

The area between the chord AB and the parabolic arc AB is called the parabolic segment.

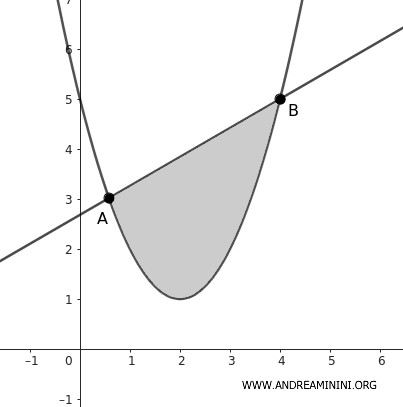
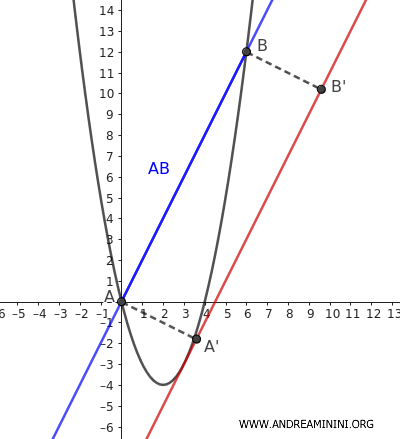
An interesting property is that the area of the parabolic segment is equal to 2/3 of the area of the rectangle ABB'A' formed by projecting points A and B onto the tangent line to the parabola parallel to the chord.

$$ A_s = \frac{2}{3} ( \overline{AB} \cdot \overline{AA'} ) $$

This property is derived from Archimedes' Theorem, as it was first proven by the Greek mathematician in the 3rd century BC.

Alternatively, the area of the parabolic segment can also be calculated using integral calculus.

The Area of the Parabolic Segment

The formula to calculate the area of a parabolic segment is a bit more complex than that for a circle.

If we have a parabola with the equation \( y = ax^2 \) and the chord runs from \( x = x_1 \) to \( x = x_2 \), with \( x_1 < x_2 \), then the area of the parabolic segment is given by:

$$ A_s = \frac{a}{3} \cdot (x_2^3 - x_1^3) $$

Note that if the chord runs from \( x = -k \) to \( x = k \), the previous formula becomes $$ A_s = \frac{a}{3} \cdot (k^3 - (-k)^3) $$ $$ A_s = \frac{a}{3} \cdot (k^3 + k^3) $$ $$ A_s = \frac{a}{3} \cdot (2k^3) $$ $$ A_s = \frac{2}{3} \cdot a \cdot k^3 $$

A Practical Example

Consider a parabola

$$ y = x^2 - 4x $$

and a secant line

$$ y = 2x $$

We need to calculate the area of the parabolic segment.

First, we find the points of intersection, which are the common points between the parabola and the secant line:

$$ \begin{cases} y = x^2 - 4x \\ \\ y = 2x \end{cases} $$

$$ \begin{cases} y = x^2 - 4x \\ \\ x^2 - 4x = 2x \end{cases} $$

$$ \begin{cases} y = x^2 - 4x \\ \\ x^2 - 6x = 0 \end{cases} $$

$$ \begin{cases} y = x^2 - 4x \\ \\ x(x - 6) = 0 \end{cases} $$

The second equation solves for \( x = 0 \) and \( x = 6 \)

$$ x = \begin{cases} x_1 = 0 \\ \\ x_2 = 6 \end{cases} $$

Substitute \( x_1 = 0 \) and \( x_2 = 6 \) into the line equation \( y = 2x \) to find the y-coordinates:

$$ y_1 = 2 x_1 = 2 \cdot 0 = 0 $$

$$ y_2 = 2 x_2 = 2 \cdot 6 = 12 $$

Thus, the points of intersection between the line and the parabola are at coordinates A(x₁, y₁) = (0, 0) and B(x₂, y₂) = (6, 12)

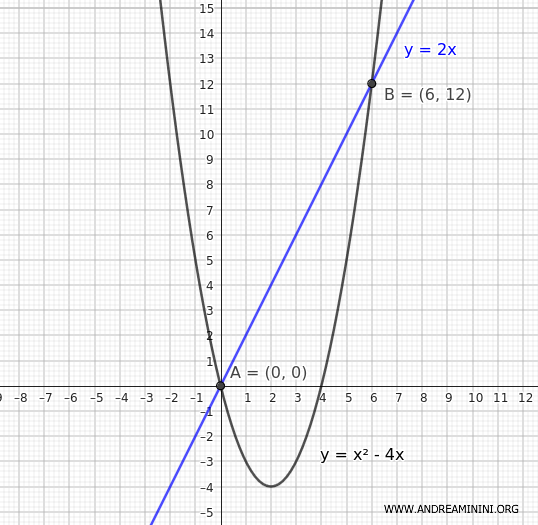
Next, we measure the distance between the ends of the chord:

$$ \overline{AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$

$$ \overline{AB} = \sqrt{(6 - 0)^2 + (12 - 0)^2} $$

$$ \overline{AB} = \sqrt{6^2 + 12^2} $$

$$ \overline{AB} = \sqrt{36 + 144} $$

$$ \overline{AB} = \sqrt{180} $$

$$ \overline{AB} = \sqrt{2^2 \cdot 3^2 \cdot 5} $$

$$ \overline{AB} = 2 \cdot 3 \cdot \sqrt{5} $$

$$ \overline{AB} = 6 \cdot \sqrt{5} $$

So, the length of the chord \( \overline{AB} \) is \( 6 \cdot \sqrt{5} \)

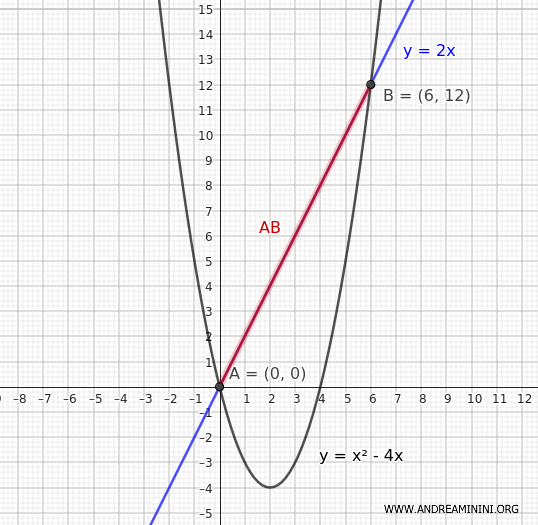
Now, let's find the equation of a line parallel to \( y = 2x \) that is tangent to the parabola \( y = x^2 - 4x \)

The equation of the line parallel to \( y = 2x \) is:

$$ y = 2x + q $$

The tangency condition between a line and a parabola is obtained by equating the equations and setting the discriminant to zero \( \Delta = 0 \)

$$ 2x + q = x^2 - 4x $$

$$ x^2 - 4x - 2x - q = 0 $$

$$ x^2 - 6x - q = 0 $$

We need to find the value of \( q \) that makes the discriminant of this quadratic equation zero.

$$ \Delta = b^2 - 4ac = 0 $$

In this case, \( a = 1 \), \( b = -6 \), and \( c = -q \)

$$ \Delta = b^2 - 4ac = 0 $$

$$ (-6)^2 - 4 \cdot 1 \cdot (-q) = 0 $$

$$ 36 + 4q = 0 $$

$$ q = \frac{-36}{4} = -9 $$

So, the equation of the line parallel to \( y = 2x \) and tangent to the parabola \( y = x^2 - 4x \) has a constant term \( q = -9 \)

$$ y = 2x + q $$

$$ y = 2x - 9 $$

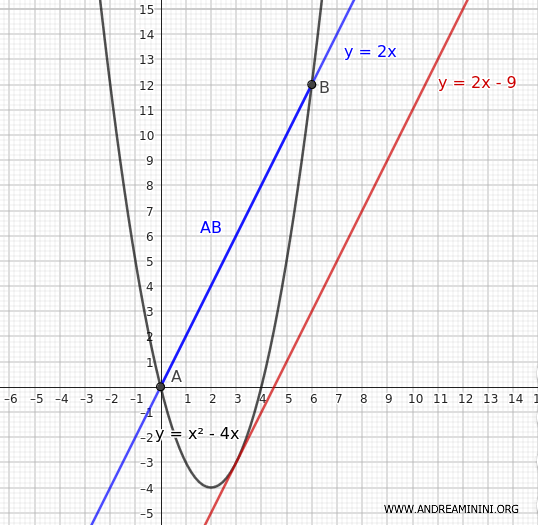
Next, we calculate the distance between the line \( y = 2x \) and the parallel line \( y = 2x - 9 \)

$$ d = \frac{|c_2 - c_1|}{\sqrt{1 + m^2}} $$

Where the constants are \( c_1 = 0 \) and \( c_2 = -9 \) while the slope of the two lines is \( m = 2 \).

$$ d = \frac{|-9 - 0|}{\sqrt{1 + 2^2}} $$

$$ d = \frac{9}{\sqrt{5}} $$

Verification. Take any point on the line \( y - 2x = 0 \), for example, P(x₀, y₀) = (0, 0). Then calculate the distance of point P(0, 0) from the parallel line \( y - 2x + 9 = 0 \) using the formula $$ d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} $$ where \( a = 1 \), \( b = -2 \), \( c = 9 \) $$ d = \frac{|1 \cdot 0 + (-2) \cdot 0 + 9|}{\sqrt{1^2 + (-2)^2}} $$ $$ d = \frac{9}{\sqrt{5}} $$

So, the distance between the two lines is \( d = \overline{AA'} = \overline{BB'} = \frac{9}{\sqrt{5}} \)

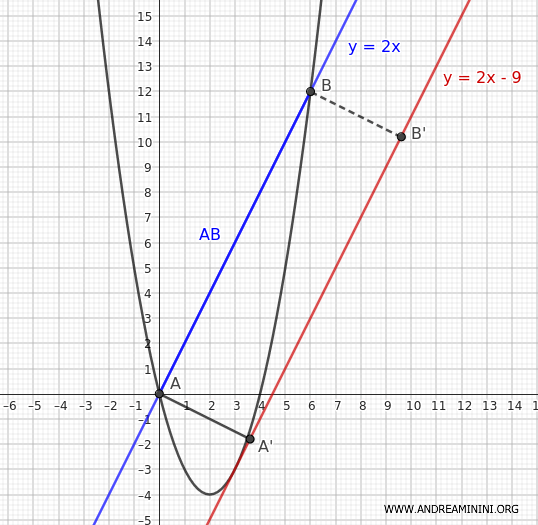
At this point, we know the base AB and the height \( d = AA' \) of the rectangle ABB'A'

$$ \overline{AB} = 6 \cdot \sqrt{5} $$

$$ \overline{AA'} = \frac{9}{\sqrt{5}} $$

Knowing that the area of the parabolic segment is 2/3 of the area of the rectangle ABB'A'

$$ A_s = \frac{2}{3} \cdot ( \overline{AB} \cdot \overline{AA'} ) $$

$$ A_s = \frac{2}{3} \cdot 6 \cdot \sqrt{5} \cdot \frac{9}{\sqrt{5}} $$

$$ A_s = \frac{2}{3} \cdot 6 \cdot 9 $$

$$ A_s = \frac{2}{3} \cdot 54 $$

$$ A_s = 36 $$

Therefore, the area of the parabolic segment is 36.

Alternative Solution

The same problem could also be solved using the formula

$$ A_s = \frac{a}{3} \cdot (x_2^3 - x_1^3) $$

Where \( j \) and \( k \) are the x-coordinates of the first and second intersection points between the chord and the parabola.

Consider the parabola

$$ y = x^2 - 4x $$

and the secant line

$$ y = 2x $$

We already calculated the intersection points in the previous example, which are at coordinates \( A(x_1, y_1) = (0, 0) \) and \( B(x_2, y_2) = (6, 12) \)

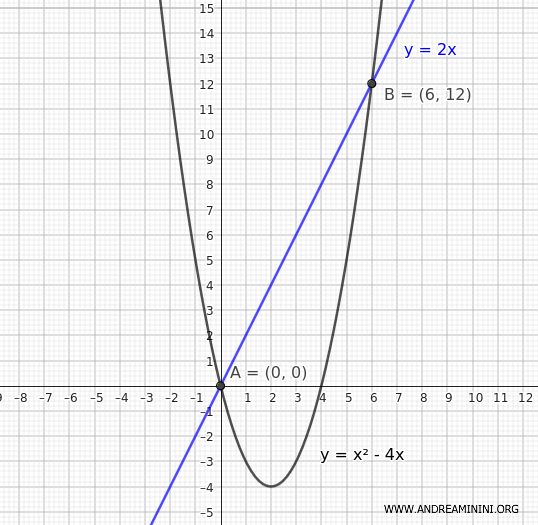
Now, apply the formula with \( x_1 = 0 \) and \( x_2 = 6 \)

$$ A_s = \frac{a}{3} \cdot (6^3 - 0^3) $$

$$ A_s = \frac{a}{3} \cdot (108) $$

The general equation for the secant line is \( y - 2x = 0 \), so the coefficient \( a = 1 \)

$$ A_s = \frac{1}{3} \cdot (108) $$

$$ A_s = 36 $$

The area of the parabolic segment is 36, the same result.

Calculating the Area of the Parabolic Segment Using Integrals

The area of the parabolic segment can also be calculated using integrals.

The area of the parabolic segment is equal to the difference between the area of the trapezoid ABCD formed by the chord AB and the x-axis and the integral of the parabola between \( x_1 \) and \( x_2 \) $$ Area(segment) = Area(ABCD) - \int_{x_1}^{x_2} ax^2 + bx + c $$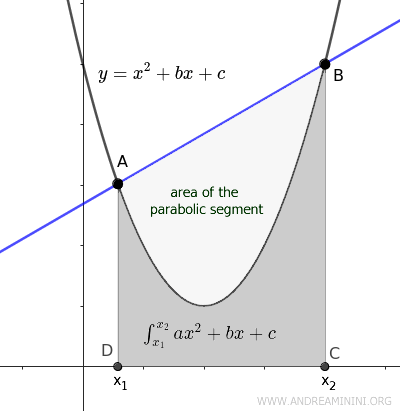

In general, the integral of the parabola calculates the area between the parabola and the x-axis when the parabola lies in the positive y-axis.

Therefore, the area of the parabolic segment can be obtained by subtracting the area under the parabola from the area of the trapezoid ABCD.

Note. The calculation of the parabolic segment using the integral is correct even when the parabola lies partially in the negative y-axis. In this case, the integral calculates the difference between the area between the parabola and the x-axis in the positive and negative y-axis. In the next example, I will provide a practical case of this scenario.

Example

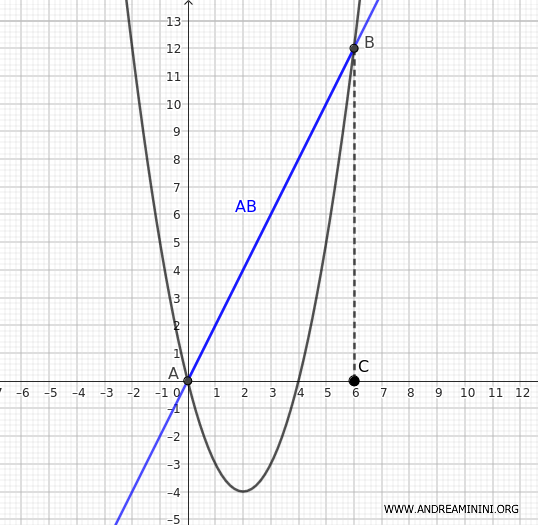
Consider the parabola \( y = x^2 - 4x \) and the secant line \( y = 2x \). The line intersects the parabola at coordinates \( A(x_1, y_1) = (0, 0) \) and \( B(x_2, y_2) = (6, 12) \).

Now let's calculate the area of the parabolic segment by subtracting the area under the parabola from the area of the trapezoid.

1] Calculate the area of the trapezoid

The area of the trapezoid \( A_{\text{trapezio}} \) is given by the average of the bases multiplied by the height divided by two:

$$ A_{\text{trapezio}} = \frac{(b_1 + b_2) \cdot h}{2} $$

The shorter base is \( b_1 = y_1 = 0 \), the longer base is \( b_2 = y_2 = 12 \), and the height is \( x_2 - x_1 = 6 - 0 = 6 \).

$$ A_{\text{trapezio}} = \frac{(0 + 12) \cdot 6}{2} $$

$$ A_{\text{trapezio}} = 36 $$

Thus, the area of the trapezoid is 36

Note that in this particular case, the trapezoid formed between the chord and the x-axis degenerates into a simple triangle ABC

2] Calculate the area under the parabola

To calculate the area under the parabola \( y = x^2 - 4x \) between \( x_1 = 0 \) and \( x_2 = 6 \), we need to integrate the function:

\[ A_{\text{parabola}} = \int_{0}^{6} (x^2 - 4x) \, dx \]

Calculate the integral:

\[ A_{\text{parabola}} = \int_{0}^{6} x^2 \, dx - \int_{0}^{6} 4x \, dx \]

The integral of \( x^2 \) is \( \frac{x^3}{3} \) and the integral of \( 4x \) is \( 2x^2 \):

\[ A_{\text{parabola}} = \left[ \frac{x^3}{3} \right]_{0}^{6} - \left[ 2x^2 \right]_{0}^{6} \]

Calculate the values:

\[ \left[ \frac{x^3}{3} \right]_{0}^{6} = \frac{6^3}{3} - \frac{0^3 }{3} = \frac{216}{3} = 72 \]

\[ \left[ 2x^2 \right]_{0}^{6} = 2 \cdot 6^2 - 2 \cdot 0^2 = 2 \cdot 36 = 72 \]

Thus, the area under the parabola is 72

\[ A_{\text{parabola}} = 72 - 72 = 0 \]

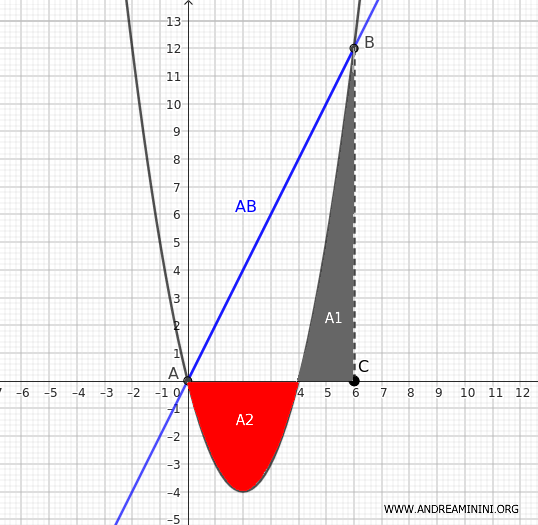
Note. When calculating the definite integral, the area \( A_1 \) between the parabola and the x-axis in the positive y-axis is calculated with a positive sign, while the area \( A_2 \) between the parabola and the x-axis in the negative y-axis is calculated with a negative sign. Therefore, the definite integral is equal to the difference \( A_1 - A_2 \). In this particular case, the definite integral does not properly measure the area under the parabola. It is important to remember that the definite integral measures the area under the parabola only when it is on the positive y-axis.

3] Calculate the area of the parabolic segment

The area of the parabolic segment is the difference between the area of the trapezoid and the integral of the parabola:

$$ Area(segment) = Area(ABCD) - \int_{x_1}^{x_2} ax^2 + bx + c $$

$$ Area(segment) = 36 - 0 = 36 $$

Therefore, the area of the parabolic segment is \( 36 \).

And so on.