Tangent, Secant, or External Line to a Parabola

A line can be tangent, secant, or external to a parabola if it intersects the parabola at one point, two points, or no points, respectively.

To find the points of intersection, you need to solve a quadratic equation.

$$ ax^2+x \cdot (b-m)+c-q=0 $$

Where $ a $, $ b $, and $ c $ are the coefficients of the parabola's equation $ y = ax^2 + bx + c $, and $ m $ and $ q $ are the slope and y-intercept of the line's equation $ y = mx + q $, respectively.

The equation will have one, two, or no solutions if the discriminant $ \Delta = b^2 - 4ac $ is equal to zero, greater than zero, or less than zero.

• If $ \Delta = 0 $, the line is tangent to the parabola because the equation has one real solution, meaning the line and the parabola intersect at exactly one point.
  
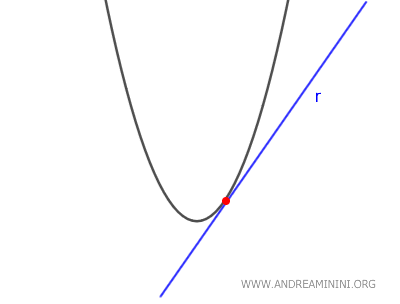
• If $ \Delta > 0 $, the line is secant to the parabola because the equation has two distinct real solutions, meaning the line intersects the parabola at two points.
  
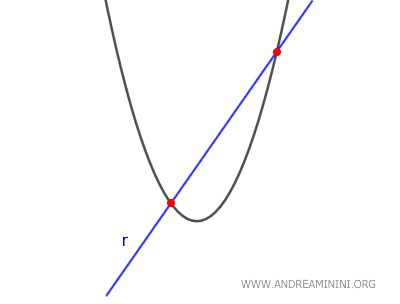
• If $ \Delta < 0 $, the line is external to the parabola because the equation has no real solutions, meaning the line does not intersect the parabola at any point.
  

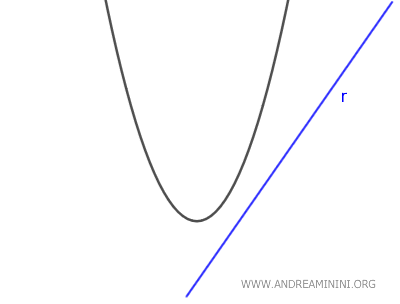
Note: This criterion applies only if the line is not parallel to the y-axis, because a vertical line cannot be represented by the explicit equation $ y = mx + q $.

A Practical Example

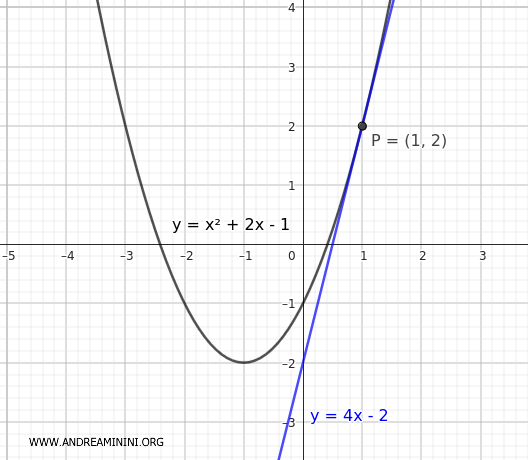
Consider a parabola with the following equation:

$$ y = x^2 + 2x - 1 $$

and a line with the equation:

$$ y = 4x - 2 $$

We need to determine if the line is tangent, secant, or external to the parabola.

To find any points of intersection, we set the two equations equal to each other:

$$ x^2 + 2x - 1 = 4x - 2 $$

$$ x^2 + 2x - 1 - 4x + 2 = 0 $$

$$ x^2 - 2x + 1 = 0 $$

Next, we calculate the discriminant of this quadratic equation:

$$ \Delta = b^2 - 4ac $$

In this case, the coefficients are a=1, b=-2, c=1:

$$ \Delta = (-2)^2 - 4 \cdot 1 \cdot 1 $$

$$ \Delta = 4 - 4 $$

$$ \Delta = 0 $$

The discriminant is zero, indicating the equation has one real solution.

This means the line is tangent to the parabola.

To find the point of tangency, we solve the quadratic equation:

$$ x = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ x = \frac{-(-2) \pm \sqrt{0}}{2 \cdot 1} $$

$$ x = \frac{2}{2} $$

$$ x = 1 $$

Once we know the x-coordinate of the tangency point, we find the y-coordinate by substituting x=1 into the line's equation:

$$ y = 4x - 2 $$

$$ y = 4 \cdot 1 - 2 $$

$$ y = 2 $$

Therefore, the point of tangency P is at coordinates $ (x;y) = (1;2) $

The Demonstration

The equation of a parabola is:

$$ y = ax^2 + bx + c $$

The equation of a line not parallel to the y-axis is:

$$ y = mx + q $$

To find the intersection points between the line and the parabola, we need to determine which x-values satisfy both equations:

$$ y = y $$

$$ ax^2 + bx + c = mx + q $$

$$ ax^2 + bx - mx + c - q = 0 $$

$$ ax^2 + x \cdot (b - m) + c - q = 0 $$

To find the solutions of the quadratic equation, we use the formula:

$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

A quadratic equation can have one, two, or no solutions depending on whether the discriminant $ \Delta = b^2 - 4ac $ is equal to zero, greater than zero, or less than zero, respectively.

• If $ \Delta = 0 $, the equation has one real solution, so the line and the parabola intersect at one point, meaning the line is tangent to the parabola.
• If $ \Delta > 0 $, the equation has two distinct real solutions, so the line and the parabola intersect at two points, meaning the line is secant to the parabola.
• If $ \Delta < 0 $, the equation has no real solutions, so the line and the parabola do not intersect, meaning the line is external to the parabola.

And so on.