How to Determine the Equation of a Parabola Given a Point and the Directrix

To derive the equation of a parabola when you know the coordinates of the focus \((h, k)\) and the equation of the directrix \(y = d\) or \(x = d\), you can follow these steps:

• If the directrix is horizontal \(y = d\)
  You can find the equation of the parabola as follows:
  1. The distance from any point \((x, y)\) to the focus is $ \sqrt{(x - h)^2 + (y - k)^2} $
  2. The distance from any point \((x, y)\) to the directrix is $ |y - d| $
  3. The equation of the parabola is obtained by equating these distances because a parabola is the set of all points equidistant from the focus and the directrix. $$ \sqrt{(x - h)^2 + (y - k)^2} = |y - d| $$ Solving the equation: $$
     (x - h)^2 + (y - k)^2 = (y - d)^2 $$ Expanding and simplifying will give you the standard form of the parabola's equation.
• If the directrix is vertical \(x = d\)
  In this case, you can find the equation of the parabola similarly:
  1. The distance from any point \((x, y)\) to the focus is $ \sqrt{(x - h)^2 + (y - k)^2} $
  2. The distance from any point \((x, y)\) to the directrix is $ |x - d| $
  3. The equation of the parabola is obtained by equating these distances, as a parabola is defined by points that are equidistant from the focus and the directrix. $$ \sqrt{(x - h)^2 + (y - k)^2} = |x - d| $$ Solving the equation: $$ (x - h)^2 + (y - k)^2 = (x - d)^2 $$ Expanding and simplifying will give you the standard form of the parabola's equation.

A Practical Example

In this example, the focus is \( F (2, 3) \) and the directrix is \( y = 1 \).

Since the directrix is horizontal, the axis of symmetry of the parabola is parallel to the x-axis.

By definition, the distance from any point \( P(x,y) \) on the parabola to the focus \( F (2, 3) \) is equal to the distance from \( P \) to the directrix \( y = 1 \).

$$ \sqrt{(x - 2)^2 + (y - 3)^2} = |y - 1| $$

By squaring both sides of the equation, we get:

$$ \left( \sqrt{(x - 2)^2 + (y - 3)^2} \right)^2 = ( |y - 1| )^2 $$

$$ (x - 2)^2 + (y - 3)^2 = (y - 1)^2 $$

Expanding and simplifying:

$$ x^2 - 4x + 4 + y^2 - 6y + 9 = y^2 - 2y + 1 $$

$$ x^2 - 4x + 13 - 1 = -2y + 6y $$

$$ x^2 - 4x + 12 = 4y $$

$$ y = \frac{x^2}{4} - \frac{4x}{4} + \frac{12}{4} $$

$$ y = \frac{x^2}{4} - x + 3 $$

This is the equation of the parabola with focus \( (2, 3) \) and directrix \( y = 1 \).

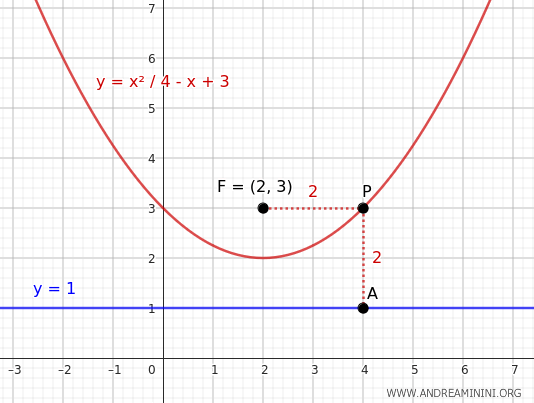
In this way, you can derive the equation of a parabola given the coordinates of the focus and the directrix.

And so on.