How to Find the Equation of a Parabola from its Vertex and Directrix
To find the equation of a parabola parallel to the y-axis when given the coordinates of the vertex $ V(h;k) $ and the equation of the directrix $ y_d $, you can use the standard form of the parabola's equation: $$ (x - h)^2 = 4p(y - k) $$ where $ p = | k-y_d | $ is the distance between the vertex and the directrix.
For a parabola with its axis of symmetry parallel to the y-axis, the directrix is horizontal because it is always perpendicular to the axis of symmetry.
The focus lies vertically opposite the vertex relative to the directrix. Therefore, the distance between the vertex $ V(h,k) $ and the directrix \(|k - y_d|\) is equal to the distance between the vertex and the focus F.
If the parabola opens upward or downward, the equation is in the form:
$$ (x - h)^2 = 4p(y - k) $$
The sign of \(p\) depends on the position of the vertex relative to the directrix:
- If \(k > y_d\), the parabola opens upward, so \(p\) is positive.
- If \(k < y_d\), the parabola opens downward, so \(p\) is negative.
Note: These steps can be adapted for other positions of the vertex and the directrix. If the directrix is vertical, the equation of the parabola will be \((y - k)^2 = 4p(x - h)\).
A Practical Example
Let's consider a vertex \( V(3, 2) \) and a directrix \( y = -1 \).
The distance between the vertex's ordinate k=2 and the directrix y=-1 is 3:
$$ p = |2 - (-1)| = 3 $$
Once this distance is found, we need to determine whether the parabola opens upward or downward to establish the sign of $ p $.
In this case, $ k > y $ since $ 2 > -1 $, so the parabola opens upward and the parameter $ p $ is positive.
$$ p = 3 $$
Now, we just need to substitute the known values into the standard form equation of the parabola.
$$ (x - h)^2 = 4p(y - k) $$
Knowing that $ p = 3 $ and the coordinates of the vertex \( V(3, 2) \) are $ h = 3 $ and $ k = 2 $:
$$ (x - 3)^2 = 4 \cdot 3 \cdot (y - 2) $$
$$ x^2 - 6x + 9 = 12y - 24 $$
$$ 12y = x^2 - 6x + 9 + 24 $$
$$ y = \frac{x^2}{12} - \frac{6x}{12} + \frac{33}{12} $$
Therefore, the equation of the parabola with vertex \((3, 2)\) and directrix \(y = -1\) is:
$$ y = \frac{x^2}{12} - \frac{x}{2} + \frac{33}{12} $$
Knowing that the focus is located in the opposite direction from the directrix $ y_d $ at the same distance $ p = 3 $ from the vertex $ V(h,k) = (3,2) $, we deduce that the focus is at the coordinates $ F(h,k+p) = (3,5) $ since $ h = 3 $ and $ k = 2 $.
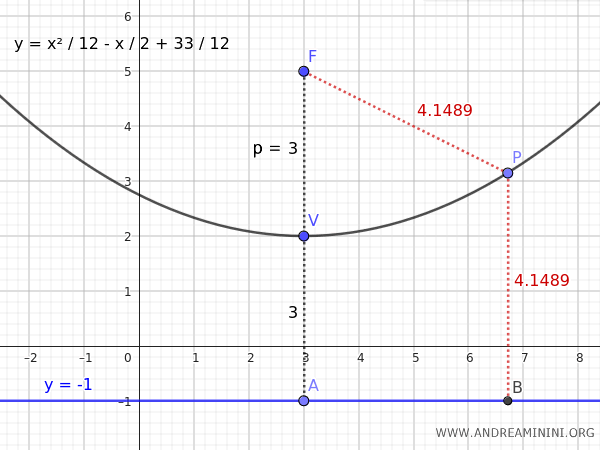
For any point $ P $ on the parabola, it is equidistant $ PF $ from the focus $ F(3;5) $ and $ PB $ from the directrix $ y_d = -1 $.
$$ \overline{PF} = \overline{PB} $$
