Equation of a Parabola Passing Through Two Points and Tangent to a Line

To determine the equation of a parabola that passes through two given points (x₁, y₁) and (x₂, y₂) and is tangent to a line r, follow these steps:

1. Write the general equation of the parabola: $$ y = ax^2 + bx + c $$
2. Use the coordinates of the known points (x₁, y₁) and (x₂, y₂) to form two equations:
3. Add the tangency condition between the parabola and the line r to the system
4. Solve the system of equations to find the coefficients a, b, and c of the parabola's equation

A Practical Example

A parabola passes through points A(2,0) and B(0,1) and is tangent to the line 4x+8y-7=0

We need to determine the equation of the parabola

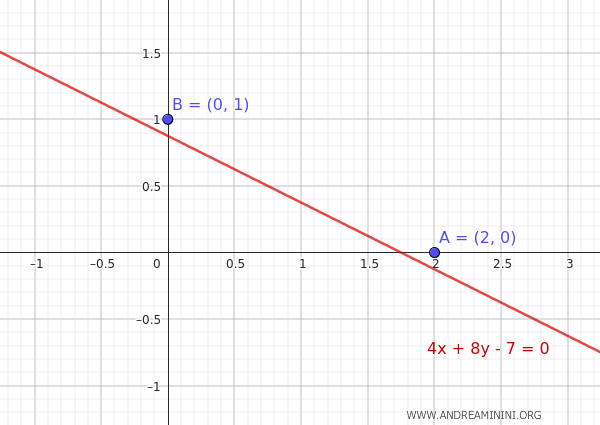
However, this initial data does not provide enough information to determine if the parabola is vertical or horizontal.

So, we need to analyze both hypotheses.

1] The Parabola is Parallel to the y-Axis

The equation of a parabola parallel to the y-axis is:

$$ y = ax^2 + bx + c $$

As a first step, substitute the coordinates of the two points A(2,0) and B(0,1) to write two equations

For point A(2,0) with x₁=2 and y₁=0

$$ y_1 = ax_1^2 + bx_1 + c $$

$$ 0 = a(2)^2 + b(2) + c $$

$$ 4a + 2b + c = 0 $$

For point B(0,1) with x₂=0 and y₂=1

$$ y_2 = ax_2^2 + bx_2 + c $$

$$ 1 = a(0)^2 + b(0) + c $$

$$ c = 1 $$

Write a system of equations

$$ \begin{cases} 4a + 2b + c = 0 \\ \\ c=1 \end{cases} $$

We must also add the condition that the parabola is tangent to the line 4x+8y-7=0

Write the equation of the line in form

$$ y = -\frac{4x}{8}+ \frac{7}{8} $$

$$ y = -\frac{x}{2}+ \frac{7}{8} $$

Then, set the equation of the line equal to the equation of the parabola to find the common points

$$ ax^2 + bx + c = -\frac{x}{2}+ \frac{7}{8} $$

$$ ax^2 + bx + c + \frac{x}{2} - \frac{7}{8} = 0 $$

$$ ax^2 + (b+\frac{1}{2}) x + c - \frac{7}{8} = 0 $$

This quadratic equation identifies the secant or tangent points between the line and the parabola.

To find only the tangent points, we must add the tangency condition, meaning the discriminant of the equation must be zero $ \Delta = 0 $.

$$ \Delta = (b+\frac{1}{2})^2 - 4 \cdot a \cdot (c- \frac{7}{8}) = 0 $$

$$ \Delta = b^2 + 2 \cdot \frac{1}{2} b + \frac{1}{4} - 4ac + \frac{7a}{2} = 0 $$

$$ \Delta = b^2 + b + \frac{1}{4} - 4ac + \frac{7a}{2} = 0 $$

Add the tangency condition to the system of equations.

$$ \begin{cases} 4a + 2b + c = 0 \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} - 4ac + \frac{7a}{2} = 0 \end{cases} $$

Then, solve the system to find the coefficients a, b, and c of the parabola

$$ \begin{cases} 4a + 2b + 1 = 0 \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} - 4a + \frac{7a}{2} = 0 \end{cases} $$

$$ \begin{cases} 4a + 2b + 1 = 0 \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} - \frac{1}{2}a = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} - \frac{1}{2}a = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} - \frac{1}{2} \cdot \frac{-2b - 1}{4} = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} + \frac{2b + 1}{8} = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + b + \frac{1}{4} + \frac{b}{4} + \frac{1}{8} = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + \frac{4b+b}{4} + \frac{2+1}{8} = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + \frac{5b}{4} + \frac{3}{8} = 0 \end{cases} $$

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b^2 + \frac{5}{4}b + \frac{3}{8} = 0 \end{cases} $$

The third equation is a quadratic equation with the discriminant

$$ \Delta = ( \frac{5}{4})^2 - 4 \cdot 1 \cdot \frac{3}{8} $$

$$ \Delta = \frac{25}{16} - \frac{12}{8} $$

$$ \Delta = \frac{25-24}{16} $$

$$ \Delta = \frac{1}{16} $$

So the solutions are

$$ b = \frac{ - \frac{5}{4} \pm \sqrt{ \frac{1}{16} } }{2} $$

$$ b = \frac{ - \frac{5}{4} \pm \frac{1}{4} }{2} = \begin{cases} \frac{-1}{2} = - \frac{1}{2} \\ \\ \frac{- \frac{6}{4}}{2} = - \frac{6}{8} = - \frac{3 }{4} \end{cases} $$

Therefore, the equations of the system are:

$$ \begin{cases} a = \frac{-2b - 1}{4} \\ \\ c=1 \\ \\ b = \begin{cases} - \frac{1}{2} \\ \\ - \frac{3}{4} \end{cases} \end{cases} $$

So, there are two possible solutions:

• If $ b = - \frac{1}{2} $ then $ a = \frac{-2 \cdot (- \frac{1}{2} ) - 1}{4} = \frac{+1 - 1}{4} = 0 $ In this case, the coefficients of the parabola are $ a=0 $, $b = - \frac{1}{2} $, $ c = 1 $. However, this solution must be excluded because the coefficient $ a=0$ cannot be zero in a parabola.
• If $ b = - \frac{3}{4} $ then $ a = \frac{-2 \cdot (- \frac{3}{4}) - 1}{4} = \frac{ \frac{3}{2} - 1 }{4} = \frac{1}{8} $ In this case, the coefficients of the parabola are $ a= \frac{1}{8} $, $ b = - \frac{3}{4} $, $ c = 1 $. Therefore, the equation of the parabola is $$ y = ax^2 + bx + c $$ $$ y = \frac{1}{8}x^2 - \frac{3}{4} x + 1 $$ Here is the graphical representation. The parabola is tangent to the line 4x+8y-7=0 and passes through the given points A(2,0) and B(0,1).
  

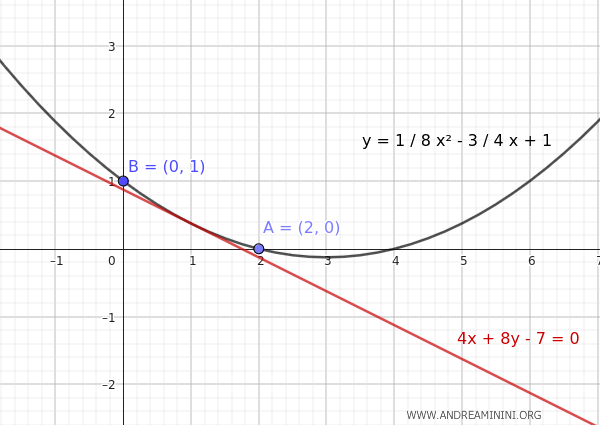
Note. Alternatively, to find the tangency condition, you could write the equation of the line in explicit form as $$ y = -\frac{x}{2}+ \frac{7}{8} $$ Therefore, the slope of the line is $ - \frac{1}{2} $. Knowing that at a tangent point, the slope between a curve and a line is the same, you could calculate the derivative of the parabola representing its slope and find the values that make it equal to that of the line. The derivative of the parabola \(y = ax^2 + bx + c\) is: $$ y' = 2ax + b $$ Therefore, the tangency condition \(y' = 2\) for the tangent point is $$ 2ax + b = 2 $$ $$ b = 2 - 2ax $$ In this case, the system to solve is $$ \begin{cases} 4a + 2b + c = 0 \\ \\ c=1 \\ \\ b = 2 - 2ax \end{cases} $$ The final solution is always the same. However, in this case, the variable x also appears and the calculations could be longer.

2] The Parabola Parallel to the X-Axis

The equation of a parabola that is parallel to the x-axis is:

$$ x = ay^2 + by + c $$

Let's substitute the coordinates of points A(2,0) and B(0,1) into the equation:

For point A(2,0) where x₁=2 and y₁=0:

$$ x_1 = ay_1^2 + by_1 + c $$

$$ 2 = a(0)^2 + b(0) + c $$

$$ c = 2 $$

For point B(0,1) where x₂=0 and y₂=1:

$$ x_2 = ay_2^2 + by_2 + c $$

$$ 0 = a(1)^2 + b(1) + c $$

$$ a + b + c = 0 $$

We now have a system of equations:

$$ \begin{cases} c = 2 \\ \\ a + b + c = 0 \end{cases} $$

Next, we add the condition of tangency between the parabola and the line 4x + 8y - 7 = 0.

We rewrite the line equation in this form:

$$ x = \frac{7 - 8y}{4} $$

$$ x = \frac{7}{4} - 2y $$

The equations of the line and the parabola intersect (either as secants or tangents) when:

$$ ay^2 + by + c = \frac{7}{4} - 2y $$

$$ ay^2 + by + c - \frac{7}{4} + 2y = 0 $$

$$ ay^2 + (b + 2)y + c - \frac{7}{4} = 0 $$

We are interested in the points of tangency, where the discriminant of the quadratic equation $ ay^2 + (b+2)y + c - \frac{7}{4} = 0 $ is zero, i.e., $ \Delta = 0 $.

$$ \Delta = (b+2)^2 - 4 \cdot a \cdot (c - \frac{7}{4}) = 0 $$

So, we add this to our system of equations:

$$ \begin{cases} c = 2 \\ \\ a + b + c = 0 \\ \\ (b + 2)^2 - 4 \cdot a \cdot (c - \frac{7}{4}) = 0 \end{cases} $$

Now we solve the system to find the coefficients a, b, and c.

$$ \begin{cases} c = 2 \\ \\ a + b + 2 = 0 \\ \\ (b + 2)^2 - 4 \cdot a \cdot (2 - \frac{7}{4}) = 0 \end{cases} $$

$$ \begin{cases} c = 2 \\ \\ a + b + 2 = 0 \\ \\ b^2 + 4b + 4 - 4 \cdot a \cdot (\frac{8 - 7}{4}) = 0 \end{cases} $$

$$ \begin{cases} c = 2 \\ \\ a = -2 - b \\ \\ b^2 + 4b + 4 - a = 0 \end{cases} $$

$$ \begin{cases} c = 2 \\ \\ a = -2 - b \\ \\ b^2 + 4b + 4 + 2 + b = 0 \end{cases} $$

$$ \begin{cases} c = 2 \\ \\ a = -2 - b \\ \\ b^2 + 5b + 6 = 0 \end{cases} $$

The quadratic equation $ b^2 + 5b + 6 = 0 $ has the following discriminant:

$$ \Delta = (5)^2 - 4 \cdot 1 \cdot 6 = 25 - 24 = 1 $$

Therefore, the equation has two solutions:

$$ b = \frac{-5 \pm \sqrt{1}}{2} $$

$$ b = \frac{-5 \pm 1}{2} = \begin{cases} \frac{-5 - 1}{2} = -3 \\ \\ \frac{-5 + 1}{2} = -2 \end{cases} $$

Thus, there are two possible solutions:

• If $ b = -3 $, then $ a = -2 - b = -2 - (-3) = 1 $. In this case, the coefficients of the parabola are $ a = 1 $, $ b = -3 $, and $ c = 2 $. So, the equation of the parabola is $$ x = ay^2 + by + c $$ $$ x = y^2 - 3y + 2 $$
• If $ b = -2 $, then $ a = -2 - b = -2 - (-2) = 0 $. In this case, the coefficients of the parabola are $ a = 0 $, $ b = -2 $, and $ c = 2 $. However, this solution must be discarded because a parabola cannot have the coefficient $ a = 0 $.

Here is the graph of the parabola:

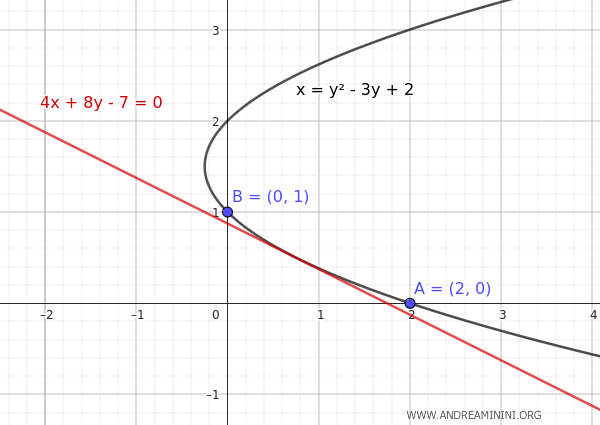
In this case, the parabola is horizontal, passing through points A(2,0) and B(0,1), and is tangent to the line 4x + 8y - 7 = 0. 

And so on.