Parabola Tangent Line Formula
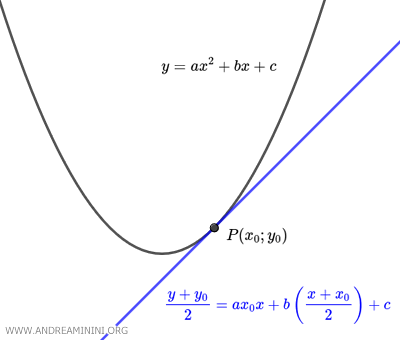
The tangent line formula for a parabola helps you determine the equation of the tangent line at a point $ P(x_0;y_0) $ on the parabola. $$ \frac{y+y_0}{2} = ax_0 x + b \left( \frac{x+x_0}{2} \right) + c $$ Here, a, b, and c are the coefficients of the parabola $ y = ax^2+bx+c $.
This formula can be derived from the general equation of a parabola:
$$ y = ax^2+bx+c $$
We replace the quadratic and linear terms as follows:
$$ x^2 \rightarrow x_0x $$
$$ x \rightarrow \frac{x+x_0}{2} $$
$$ y \rightarrow \frac{y+y_0}{2} $$
Therefore, the equation of the parabola becomes:
$$ \frac{y+y_0}{2} = ax_0 x + b \left( \frac{x+x_0}{2} \right) + c $$
Note: The tangent line formula is only applicable for finding the tangent line at a point on the parabola. It cannot be used for points outside the parabola. Generally, it is a specific application of the tangent line formula for conic sections to the case of a parabola.
A Practical Example
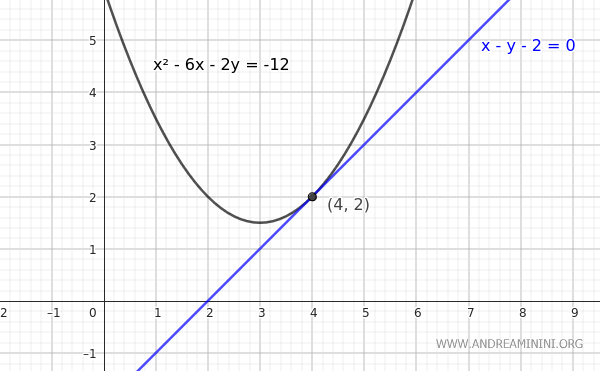
Consider the parabola:
$$ x^2-6x-2y = -12 $$
We rewrite it in its general form:
$$ x^2-6x-2y +12 = 0 $$
We want to find the equation of the tangent line at the point $ P(4;2) $ on the parabola.
Note: First, we verify that the point P(4;2) lies on the parabola by substituting x=4 and y=2 into the equation. $$ (4)^2-6 \cdot 4-2 \cdot 2 = -12 $$ $$ 16-24-4 = -12 $$ $$ -12 = -12 $$ The equation holds, so P(4;2) is on the parabola. As a reminder, the tangent line formula only applies to points on the parabola, not external points.
We substitute the quadratic term $ x^2 \rightarrow x_0x $ in the equation:
$$ x_0x-6x-2y + 12 = 0 $$
Next, we substitute the linear term $ x \rightarrow \frac{x+x_0}{2} $:
$$ x_0x-6 \cdot \frac{x+x_0}{2} -2y + 12 = 0 $$
$$ x_0x-3(x+x_0) -2y + 12 = 0 $$
Then, we substitute the linear term $ y \rightarrow \frac{y+y_0}{2} $:
$$ x_0x-3(x+x_0) -2 \cdot \frac{y+y_0}{2} + 12 = 0 $$
$$ x_0x-3(x+x_0) -y - y_0 + 12 = 0 $$
The point of tangency is at $ P(4;2) $, so $ x_0=4 $ and $ y_0=2 $:
$$ 4x-3(x+4) -y - 2 + 12 = 0 $$
$$ 4x-3x-12 -y + 10 = 0 $$
$$ x -y - 2 = 0 $$
This is the equation of the tangent line to the parabola at point P(4;2).
The Proof
To prove the tangent line formula for a parabola, we start with its general equation:
$$ y = ax^2+bx+c $$
Consider a point $ P(x_0;y_0 ) $.
The family of lines passing through P is given by:
$$ y-y_0 = m (x-x_0) $$
To find the lines that intersect the parabola (both secants and tangents) and pass through P, we solve the system:
$$ \begin{cases} y = ax^2+bx+c \\ \\ y = m(x-x_0)+y_0 \end{cases} $$
The resulting equation is:
$$ ax^2+bx+c = m(x-x_0)+y_0 $$
$$ ax^2+bx+c - m(x-x_0)-y_0 = 0 $$
$$ ax^2+bx+c - mx + mx_0-y_0 = 0 $$
$$ ax^2+x(b-m)+ mx_0-y_0 +c = 0 $$
For a quadratic equation $ Ax^2+Bx+C=0 $, if the discriminant is greater than zero $ \Delta>0 $, the sum of the roots $ x_1 $ and $ x_2 $ is equal to the ratio of the coefficients -B/A:
$$ x_1+x_2 = - \frac{B}{A} $$
Where A=a and B=(b-m):
$$ x_1+x_2 = - \frac{b-m}{a} $$
In this case, we are only interested in the point of tangency, not the points of intersection of the secant lines.
Thus, the solutions of the quadratic equation coincide $ x_1=x_2 $ and are equal to $ x_0 $:
$$ x_0+x_0 = - \frac{b-m}{a} $$
$$ 2x_0 = - \frac{b-m}{a} $$
From this equation, we find the slope m:
$$ m = 2ax_0 + b $$
We substitute the slope m into the family of lines equation:
$$ y-y_0 = m (x-x_0) $$
$$ y-y_0 = (2ax_0 + b) (x-x_0) $$
$$ y-y_0 = 2ax_0x - 2ax_0^2 + bx - bx_0 $$
Since point $ P(x_0;y_0) $ is on the parabola, we substitute $ x_0 $ and $ y_0 $ into the parabola's equation:
$$ y_0 = ax_0^2 + bx_0 + c $$
Multiplying both sides by two:
$$ 2y_0 = 2ax_0^2 + 2bx_0 + 2c $$
We add the two equations $ y-y_0 = m (x-x_0) $ and $ 2y_0 = 2ax_0^2 + 2bx_0 + 2c $:
\[
\begin{array}{rcl}
y - y_0 & = & 2ax_0 x - 2ax_0^2 + bx - bx_0 \\
2y_0 & = & 2ax_0^2 + 2bx_0 + 2c \\
\hline
y + y_0 & = & 2ax_0 x + bx + bx_0 + 2c
\end{array}
\]
We get the equation:
$$ y + y_0 = 2ax_0 x + bx + bx_0 + 2c $$
Dividing both sides by two:
$$ ( y + y_0 ) \cdot \frac{1}{2} = ( 2ax_0 x + bx + bx_0 + 2c ) \cdot \frac{1}{2} $$
$$ \frac{ y + y_0}{2} = \frac{2ax_0 x}{2} + \frac{bx+bx_0}{2} + \frac{2c}{2} $$
$$ \frac{y+y_0}{2} = ax_0 x + b \left( \frac{x+x_0}{2} \right) + c $$
Finally, we arrive at the formula we set out to prove.
And so on.
