How to Find the Equation of a Parabola Given the Focus and Vertex

To derive the equation of a parabola parallel to the y-axis, given the coordinates of the vertex \( V(h, k)\) and the focus \( F(h, k + p)\), follow these steps:

1. Calculate the distance from the vertex to the focus
   The distance \( p \) between the vertex and the focus is the difference between the y-coordinate of the focus ($ k+p $) and the y-coordinate of the vertex ($ k $): $$ p = (k + p) - k = p $$
2. Write the equation of the parabola
   The standard form of the equation of a parabola with vertex \((h, k)\) and an axis of symmetry parallel to the y-axis is:
   $$ (x - h)^2 = 4p(y - k) $$

Practical Example

Consider a parabola with vertex \((h, k) = (2, 3)\) and focus \((2, 5)\).

We need to find the equation of this parabola.

First, calculate the distance between the focus and the vertex:

$$ p = 5 - 3 = 2 $$

Next, write the equation of the parabola in standard form:

$$ (x - h)^2 = 4p(y - k) $$

Substituting \( p = 2 \), \( h = 2 \), and \( k = 3 \), we get:

$$ (x - 2)^2 = 8(y - 3) $$

Therefore, the equation of the parabola with vertex \((2, 3)\) and focus \((2, 5)\) is:

$$ (x - 2)^2 = 8(y - 3) $$

Expanding this equation, we have:

$$ x^2 - 4x + 4 = 8y - 24 $$

$$ 8y = x^2 - 4x + 4 + 24 $$

$$ y = \frac{x^2}{8} - \frac{4x}{8} + \frac{28}{8} $$

$$ y = \frac{x^2}{8} - \frac{x}{2} + \frac{7}{2} $$

Here is the graphical representation:

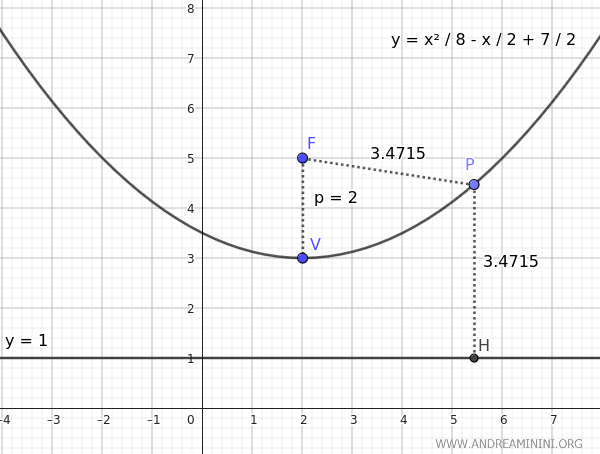
Note: Knowing that the directrix is perpendicular to the parabola's axis of symmetry and is equidistant from the vertex as the focus, we can deduce that the directrix has the equation y = 1. This allows us to verify that the distance PF from any point P to the focus F is equal to the distance PH from the same point to the directrix.

This is the method to derive the equation of a parabola given the coordinates of the vertex and the focus.

And so on.