How to Find the Equation of a Parabola Given Three Points

To determine the equation of a parabola when you know three points \( A(x_1, y_1)\), \( B(x_2, y_2)\), and \( C(x_3, y_3)\), you can use the method of simultaneous equations.

The standard form of a parabola is:

\[ y = ax^2 + bx + c \]

Given the coordinates of three distinct points \( A(x_1, y_1)\), \( B(x_2, y_2)\), and \( C(x_3, y_3)\), you can substitute each point into the parabola's equation to form a system of three linear equations:

$$ y_1 = ax_1^2 + bx_1 + c $$

$$ y_2 = ax_2^2 + bx_2 + c $$

$$ y_3 = ax_3^2 + bx_3 + c $$

These equations can be written as a system of linear equations:

$$
\begin{cases}
ax_1^2 + bx_1 + c = y_1 \\ \\ ax_2^2 + bx_2 + c = y_2 \\ \\ ax_3^2 + bx_3 + c = y_3 \\ \end{cases} $$

By solving this system, you can find the coefficients "a", "b", and "c" for the parabola's equation \( y = ax^2 + bx + c \) that passes through the three points.

A Practical Example

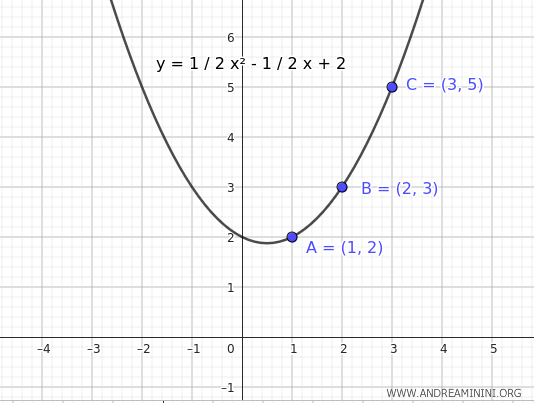
Consider three distinct points \( A(1, 2)\), \( B(2, 3)\), and \( C(3, 5)\):

Substitute the x and y coordinates of each point into the system of equations.

$$
\begin{cases}
a(1^2) + b(1) + c = 2 \\ \\
a(2^2) + b(2) + c = 3 \\ \\
a(3^2) + b(3) + c = 5 \\
\end{cases} $$

This simplifies to:

$$
\begin{cases}
a + b + c = 2 \\ \\
4a + 2b + c = 3 \\ \\
9a + 3b + c = 5 \\
\end{cases} $$

Next, solve this system to find the values of \( a \), \( b \), and \( c \) that satisfy these equations. You can use any method you prefer.

In this case, we'll use Cramer's rule.

Note: Any method for solving systems of equations will work.

Write the system in matrix form:

$$
\begin{pmatrix}
1 & 1 & 1 \\
4 & 2 & 1 \\
9 & 3 & 1 \\
\end{pmatrix}
\begin{pmatrix}
a \\
b \\
c \\
\end{pmatrix}
=
\begin{pmatrix}
2 \\
3 \\
5 \\
\end{pmatrix} $$

The determinant of the coefficient matrix is:

$$ \Delta = \begin{vmatrix}
1 & 1 & 1 \\
4 & 2 & 1 \\
9 & 3 & 1 \end{vmatrix} = 1 \cdot \begin{vmatrix} 2 & 1 \\ 3 & 1 \end{vmatrix} - 1 \cdot \begin{vmatrix} 4 & 1 \\ 9 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 4 & 2 \\ 9 & 3 \end{vmatrix} = -1 + 5 -6 = -2 $$

Next, calculate the determinants of the matrices obtained by replacing one of the columns (a, b, c) with the column of known terms (2, 3, 5) from the system:

$$ \Delta_a = \begin{vmatrix}
2 & 1 & 1 \\
3 & 2 & 1 \\
5 & 3 & 1 \end{vmatrix} = 2 \cdot \begin{vmatrix} 2 & 1 \\ 3 & 1 \end{vmatrix} - 1 \cdot \begin{vmatrix} 3 & 1 \\ 5 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 3 & 2 \\ 5 & 3 \end{vmatrix} =  -2  + 2 - 1 = -1 $$

$$ \Delta_b = \begin{vmatrix}
1 & 2 & 1 \\
4 & 3 & 1 \\
9 & 5 & 1 \end{vmatrix} = 1 \cdot \begin{vmatrix} 3 & 1 \\ 5 & 1 \end{vmatrix} - 2 \cdot \begin{vmatrix} 4 & 1 \\ 9 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 4 & 3 \\ 9 & 5 \end{vmatrix} = -2 + 10 -7 = 1 $$

$$ \Delta_c = \begin{vmatrix}
1 & 1 & 2 \\
4 & 2 & 3 \\
9 & 3 & 5 \end{vmatrix} = 1 \cdot \begin{vmatrix} 2 & 3 \\ 3 & 5 \end{vmatrix} - 1 \cdot \begin{vmatrix} 4 & 3 \\ 9 & 5 \end{vmatrix} + 2 \cdot \begin{vmatrix} 4 & 2 \\ 9 & 3 \end{vmatrix} = 1+7 -12 = -4 $$

Thus, the solutions of the system are:

$$ a = \frac{ \Delta_a  }{ \Delta } = \frac{-1}{-2} = \frac{1}{2} $$

$$ b = \frac{ \Delta_b  }{ \Delta } = \frac{1}{-2} = - \frac{1}{2} $$

$$ c = \frac{ \Delta_c  }{ \Delta } = \frac{-4}{-2} = 2 $$

This gives us the coefficients for the parabola's equation:

$$ y = ax^2+bx+c $$

$$ y = \frac{1}{2}x^2- \frac{1}{2}x +2 $$

This parabola passes through the points \( A(1, 2)\), \( B(2, 3)\), and \( C(3, 5)\)

And that's it!