Intersection of a Parabola and a Line

The intersection of a line with a parabola can occur at most in two points.

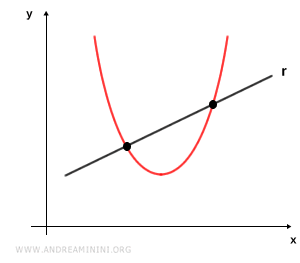
• Secant Line
  A line is called a secant if it intersects the parabola at two distinct points.
  
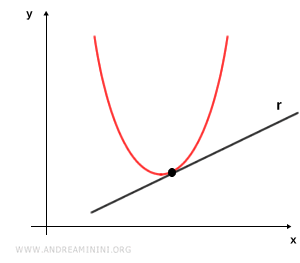
• Tangent Line
  A line is called a tangent if it intersects the parabola at exactly one point and is not parallel to the axis of the parabola.
  
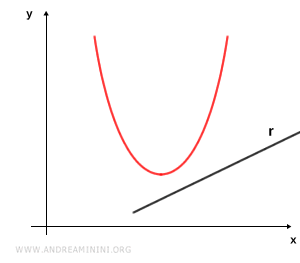
• External Line
  A line is called external if it does not intersect the parabola.
  
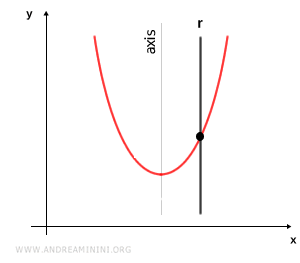
• Line Parallel to the Axis of the Parabola
  A line is called parallel to the axis of the parabola if it is parallel to the parabola's axis. Note that in this case, there is only one point of intersection, but it is not called a tangent line.
  

How to Find the Points of Intersection Between a Line and a Parabola

To find the points of intersection between a parabola and a line that is not parallel to the parabola's axis, set up a system of equations involving a quadratic equation.

$$ \begin{cases} y = ax^2 + bx + c \\ \\ y = mx + q \end{cases} $$

The first equation is the quadratic equation of the parabola.

The second equation is the linear equation of the line.

Since \( y = ax^2 + bx + c \) and \( y = mx + q \), we can set the two expressions equal:

$$ ax^2 + bx + c = mx + q $$

This yields a quadratic equation:

$$ ax^2 + bx - mx + c - q = 0 $$

$$ ax^2 + x(b - m) + (c - q) = 0 $$

Let's denote \( a' = a \), \( b' = b - m \), and \( c' = c - q \).

$$ a'x^2 + x b' + c' = 0 $$

Next, calculate the discriminant of the quadratic equation:

$$ \Delta = b'^2 - 4a'c' $$

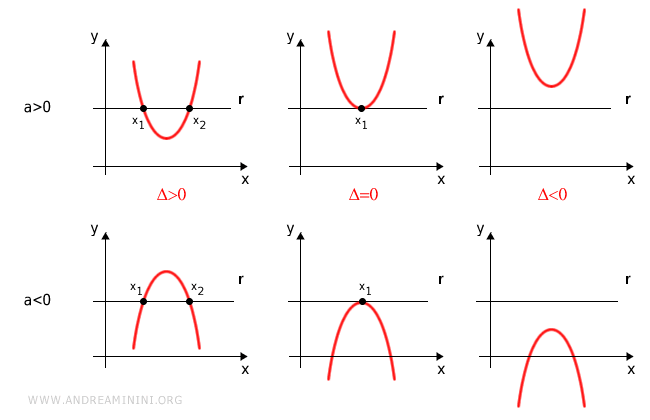
Depending on the discriminant, there are three possibilities:

• Δ > 0
  If the discriminant is positive, the line is secant to the parabola. To find the points of intersection, solve the quadratic equation for its two distinct roots.
• Δ = 0
  If the discriminant is zero, the line is tangent to the parabola. To find the point of tangency, solve the quadratic equation for its double root.
• Δ < 0
  If the discriminant is negative, the line is external to the parabola. There are no points of intersection.

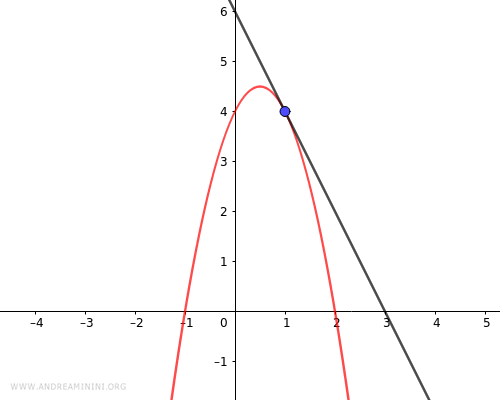
A Practical Example

Let's determine whether the line

$$ y = -2x + 6 $$

is secant, tangent, or external to the parabola

$$ y = -2x^2 + 2x + 4 $$

Setting the two expressions equal:

$$ -2x + 6 = -2x^2 + 2x + 4 $$

$$ 2x^2 - 2x - 2x + 6 - 4 = 0 $$

$$ 2x^2 - 4x + 2 = 0 $$

Calculate the discriminant of the quadratic equation:

$$ \Delta = b^2 - 4ac = (-4)^2 - 4(2)(2) = 16 - 16 = 0 $$

The discriminant is Δ = 0. Therefore, the line is tangent to the parabola.

To find the point of tangency, solve the quadratic equation for its roots:

$$ x = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ x = \frac{-(-4) \pm \sqrt{0}}{2(2)} $$

$$ x = \frac{4}{4} = 1 $$

Once we have \( x = 1 \), we can find \( y \) using either the equation of the line or the parabola. Let's use the line equation for simplicity.

$$ y = -2x + 6 $$

Knowing that \( x = 1 \):

$$ y = -2(1) + 6 $$

$$ y = 4 $$

Thus, the point of tangency is at the coordinates \( x = 1 \) and \( y = 4 \), or \((x, y) = (1, 4)\).

And that's how it's done.