How to Write the Equation of a Parabola Given a Point, the Axis, and the Directrix

To determine the equation of a parabola given a point \( P(x_0, y_0) \), the axis ($ x=h $ or $ y=k $), and the directrix, follow these steps:

• For a parabola with a vertical axis $ x_A=h $, the directrix is a horizontal line with the equation \( y_D = k - p \).
  
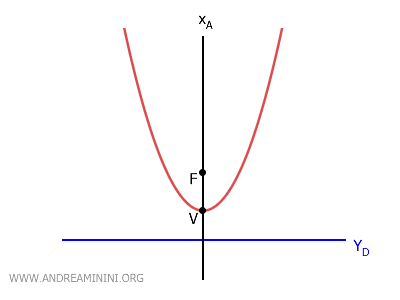
• For a parabola with a horizontal axis $ y_A=k $, the directrix is a vertical line with the equation \( x_D = h - p \).
  

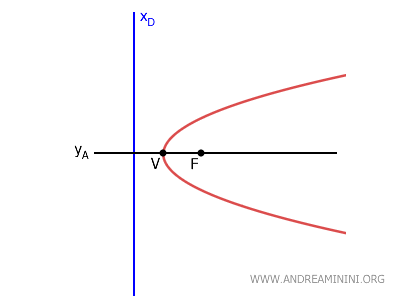
Here, $ (h, k) $ is the vertex of the parabola, while $ p $ is the distance between the focus and the vertex.

The equation of the axis helps determine if the parabola is vertical or horizontal, and thus the form of the parabola's equation.

• If the axis is vertical $ x=h $, the equation of the parabola is of the form $$ y = ax^2 + bx + c $$ and in the standard form $$ (x - h)^2 = 4p(y - k) $$
• If the axis is horizontal $ y=k $, the equation of the parabola is of the form $$ x = ay^2 + by + c $$ and in the standard form $$ (y - k)^2 = 4p(x - h) $$

Knowing the coordinates of the point and the equation of the directrix helps determine the direction in which the parabola opens.

• If the parabola is vertical and the directrix is below the y-coordinate of point P, the parabola opens upwards. Conversely, if the directrix is above the point, it opens downwards.
  
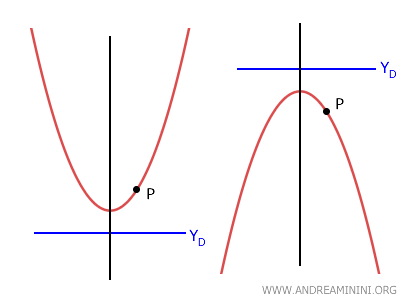
• If the parabola is horizontal and the directrix is to the left of the x-coordinate of point P, the parabola opens to the right. Conversely, if the directrix is to the right of the point, it opens to the left.
  

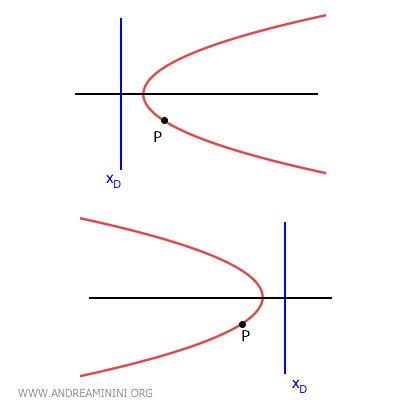
Finally, use the coordinates of point \( P(x_0, y_0) \) to determine the missing parameters.

• For a parabola with a vertical axis, substitute \( x_0 \) and \( y_0 \) into the equation \( (x_0 - h)^2 = 4p(y_0 - k) \) and solve for \( h \), \( k \), and \( p \).
• For a parabola with a horizontal axis, substitute \( x_0 \) and \( y_0 \) into the equation \( (y_0 - k)^2 = 4p(x_0 - h) \) and solve for \( h \), \( k \), and \( p \).

A Practical Example

Consider the point \( P(5, 6) \), the directrix \( y_D = 2 \), and the vertical axis \( x_A = 1 \)

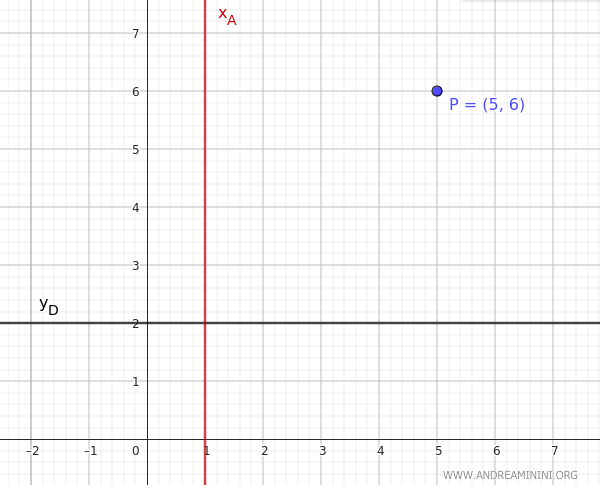
In this case, the directrix \( y_D=2 \) is horizontal, and the axis of symmetry \( x_A = 1 \) is vertical, so the parabola is vertical.

The y-coordinate of the given point \( P(5,6) \) is \( y_0=6 \), which is above the directrix \( y_D=2 \), so the parabola opens upwards.

Knowing the parabola is vertical, we can start writing the standard equation of the parabola.

$$ (x - h)^2 = 4p(y - k) $$

We don't know the coordinates of the vertex $ V(h,k) $ or the focus $ F(x_F,y_F) $.

However, since the vertex and the focus are points on the axis of symmetry $ x_A=1 $, they share the same x-coordinate, so $ h =1 $ and $ x_F = 1 $.

$$ V(h,k) = (1,k) $$

$$ F(x_F,y_F) = (1,y_F) $$

Substituting $ h = 1 $ into the equation of the parabola, we get:

$$ (x - 1)^2 = 4p(y - k) $$

The parameter $ p = y_F-k $ measures the distance between the focus $ F(x_F,y_F) $ and the vertex $ V(h,k) $.

$$ p = y_F - k $$

In this case, we don't know the y-coordinate of the focus $ F (1,y_F) $, so this isn't helpful.

However, knowing that the distance $ p = y_F - k $ between the focus and the vertex is equal to the distance $ p = k - y_D $ between the vertex $ V(h,k) = (1,k) $ and the directrix $ y_D=2 $, we can find $ p $ this way:

$$ p = k - y_D $$

$$ p = k - 2 $$

So, substituting $ p = k-2 $ into the equation of the parabola:

$$ (x - 1)^2 = 4(k-2)(y - k) $$

This reduces the number of unknowns in the equation.

Finally, since the point \( P(5, 6) \) lies on the parabola and satisfies the equation, we substitute $ x=5 $ and $ y=6 $ into the equation:

$$ (5 - 1)^2 = 4(k-2)(6 - k) $$

This allows us to solve for $ k $, the y-coordinate of the vertex $ V(h,k)=(1,k) $ that we don't yet know.

$$ 4^2 = 4(k-2)(6 - k) $$

$$ 16 = 4(k-2)(6 - k) $$

Dividing both sides of the equation by 4:

$$ 4 = (k-2)(6 - k) $$

$$ 4 = 6k - k^2 - 12 + 2k $$

$$ -k^2 + 8k - 12 - 4 = 0 $$

$$ -k^2 + 8k - 16 = 0 $$

The discriminant of the quadratic equation is:

$$ \Delta = b^2 - 4ac = 8^2 - 4 \cdot (-1) \cdot (-16) = 64 - 64 = 0 $$

So, the quadratic equation has a single solution:

$$ k = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ k = \frac{-8 \pm \sqrt{0}}{2 \cdot (-1)} $$

$$ k = \frac{-8}{-2} $$

$$ k = 4 $$

Thus, the vertex of the parabola is at coordinates $ V(h,k)=(1,4) $.

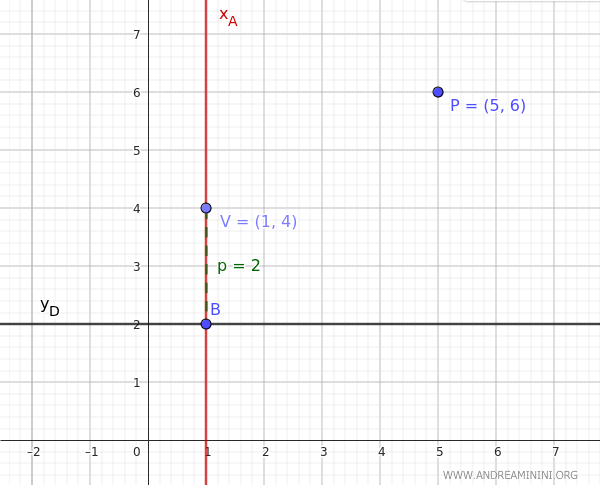
Once we know k, we can calculate the distance between the vertex and the directrix:

$$ p = k - y_D = 4 - 2 = 2 $$

At this point, we have all the necessary information ( h=1, k=4, p=2 ) to complete the standard form equation of the parabola:

$$ (x - h)^2 = 4p(y - k) $$

$$ (x - 1)^2 = 4 \cdot 2 \cdot (y - 4) $$

$$ x^2 - 2x + 1 = 8y - 32 $$

$$ x^2 - 2x + 1 + 32 - 8y = 0 $$

$$ x^2 - 2x - 8y + 33 = 0 $$

Here is the graphical representation:

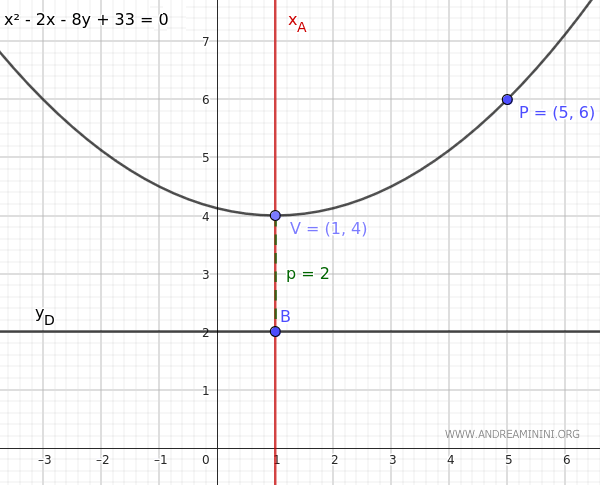
And that's how you do it.