Conic Sections
Conic sections (or simply conics) are a family of curves in a plane formed by the intersection of a right circular cone and a plane.
Depending on the inclination and position of the plane relative to the cone, different types of curves can be obtained: ellipses, parabolas, and hyperbolas.
In general, a conic section is a locus of points in the plane that satisfies the following second-degree equation:
$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$
where at least one of the coefficients A, B, or C is non-zero.
By evaluating the discriminant of a quadratic equation, one can determine the nature of its solutions.
$$ \Delta = B^2 - 4AC $$
- If $ \Delta < 0 $, the equation corresponds to an ellipse or a circle.
- If $ \Delta = 0 $, the equation corresponds to a parabola.
- If $ \Delta > 0 $, the equation corresponds to a hyperbola.
In practice, this test is useful for identifying the general geometric type (elliptic, parabolic, or hyperbolic). Nevertheless, it does not guarantee the presence of real solutions-that is, whether the curve can actually be plotted-nor does it rule out degenerate cases.
The ancient Greeks were the first to realize that certain curves could be derived from conic sections. During the Hellenistic period, around 200 B.C., Menecmus and Apollonius of Perga studied these conic sections extensively. Apollonius was the one who named the three main types of conic sections: ellipse, parabola, and hyperbola, considering the circle as a special case of the ellipse. Initially, the Greeks used different cones cut by an inclined plane to create the parabola, ellipse, and hyperbola. Apollonius showed that these curves could also be generated using a single cone (whether right or oblique) by simply varying the angle of the intersecting plane.
Characteristics of a Conic Section
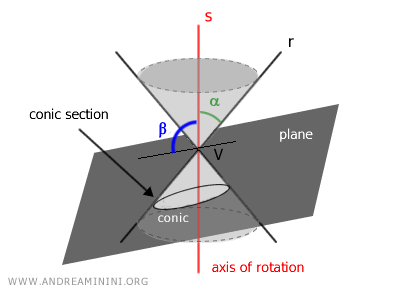
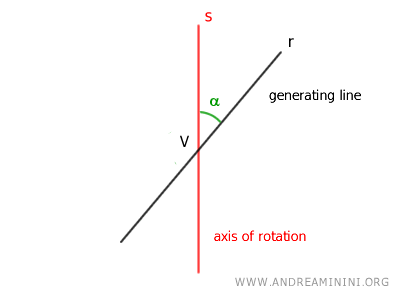
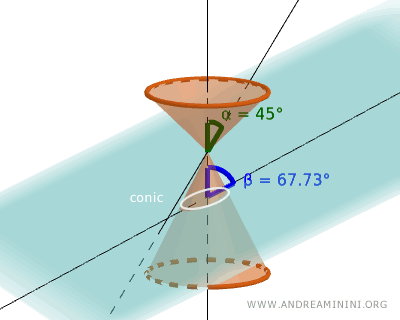
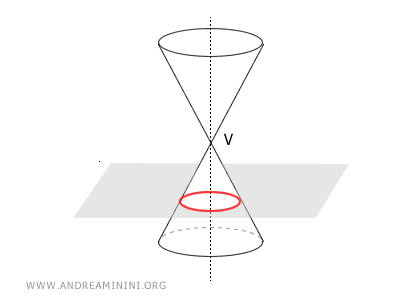
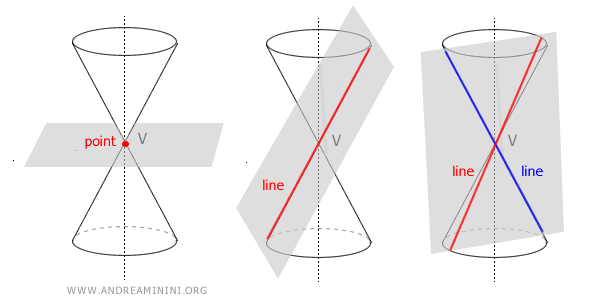
To create a conic section, intersect two lines r and s at an angle α (called the semi-aperture) at a point V in space known as the "vertex."
The complete rotation of line r around line s generates a double-napped conical surface.
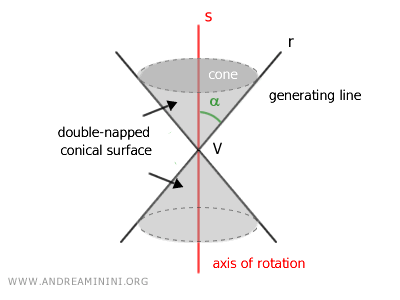
For this reason, line r is called the generating line while line s is called the axis of rotation.
The space within the surface is known as the double-napped cone.
Next, we intersect the double-napped cone with a plane at a certain inclination β with respect to the axis of symmetry.
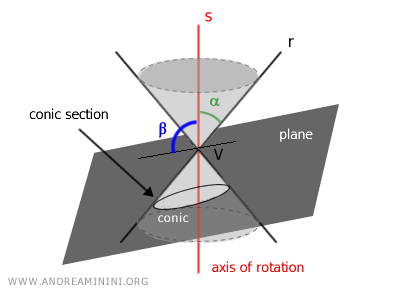
The points where the intersecting plane meets the double-napped cone generate a curve called a "conic section" or simply a "conic."
For example, the conic in the previous figure appears on the plane as follows:

Depending on the angle α of the cone (semi-aperture) and the angle β of the plane, different open or closed curves can be obtained:
- If β < α, the conic section is a hyperbola, an open curve composed of two unbounded branches, because the plane intersects both nappes of the cone.
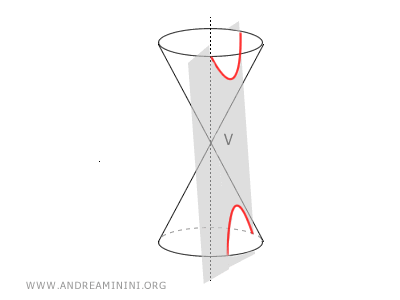
- If β = α, the conic section is a parabola, an open and unbounded curve composed of a single branch, because the plane has the same inclination as the cone's angle and intersects only one nappe of the cone.
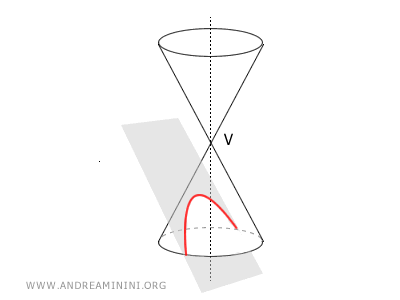
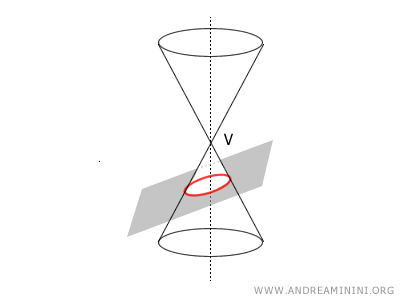
- If β > α, the conic section is an ellipse, a closed and bounded curve, because the plane's angle is greater than the semi-aperture.
Example
- If β = π/2, forming a right angle (90°), where "π" represents the number pi, the conic section is a circle, a closed and bounded curve with all points equidistant from its center.
Types of Conic Sections
Conic sections are classified based on their shape and geometric properties:
- Ellipse
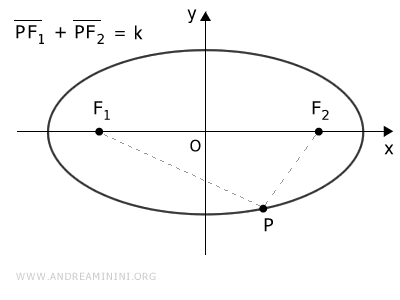
An ellipse is a closed curve obtained by intersecting a cone with a plane inclined between θ and π/2 relative to its axis. It is defined by the constant sum of the distances from its two foci. It has two axes of symmetry, major and minor. If the two axes are equal, a circle is obtained.
- Parabola
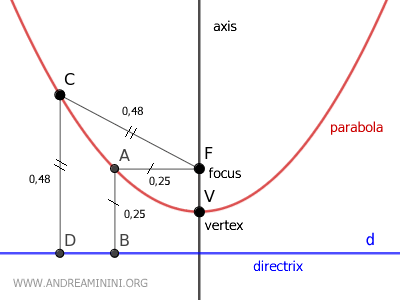
A parabola is the set of points equidistant from a focus (F) and a directrix (d). It has an axis of symmetry and is formed by intersecting a cone with a plane parallel to one of its generating lines, forming an angle θ with the axis of the conic. It is not a closed curve and belongs to only one nappe of the cone.
- Hyperbola
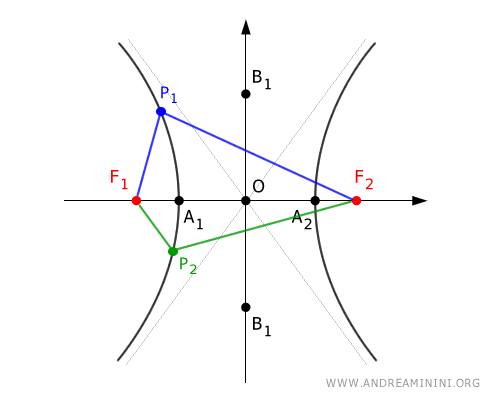
A hyperbola is formed by the intersection of a cone with a plane inclined less than θ with respect to the cone's axis. It is defined by points where the absolute value of the difference of the distances from two fixed foci is constant. It is an open curve and, because it intersects both nappes of the cone, it splits into two opposite branches with two axes of symmetry.
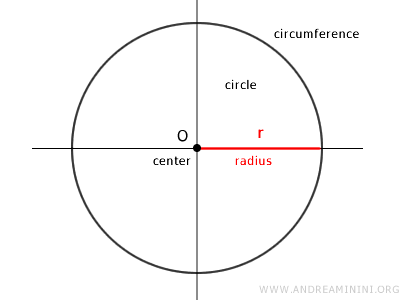
- Circle
A circle is a special case of an ellipse obtained by intersecting a right cone with a plane perpendicular to its axis. It is a closed curve.
Note. These types of conics are called "non-degenerate" to distinguish them from "degenerate" conics like a point, a line, and a pair of lines. For example, a point can be considered a degenerate conic obtained by intersecting the conic with a plane passing through the cone's vertex. The same applies to a plane intersecting a line or two lines of the conic. These cases are also referred to as "degenerate conics."
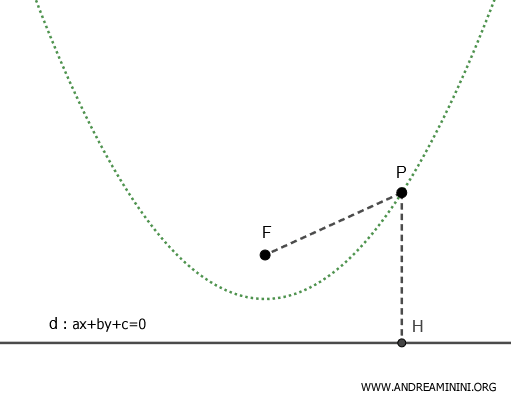
Definition of a Conic Section
For any point $ P(x;y) $ on a conic section, there is a constant ratio $$ \frac{ \overline{PF} }{ \overline{PH} } = e $$ where PF is the distance from point P to a fixed point $ F(p;q) $ known as the "focus", and PH is the distance from point P to a fixed line d: $ ax+by+c=0 $ called the "directrix" that does not pass through P.
The constant "e" is a non-negative real number that defines the eccentricity of the conic section.
The eccentricity determines the type of conic section:
- If e=0, the conic section is a circle.
- If 0<e<1, the conic section is an ellipse.
- If e=1, the conic section is a parabola.
- If e>1, the conic section is a hyperbola.
Note. A parabola has a single focus and a directrix. In contrast, an ellipse and a hyperbola each have two foci and two directrices, which are symmetrical about the center and perpendicular to the focal axis. Finally, a circle can be thought of as a conic section with a directrix at an infinite distance from its center. Technically, a circle doesn’t have just one directrix, but an infinite number, all located at an infinite distance from the center.
Example
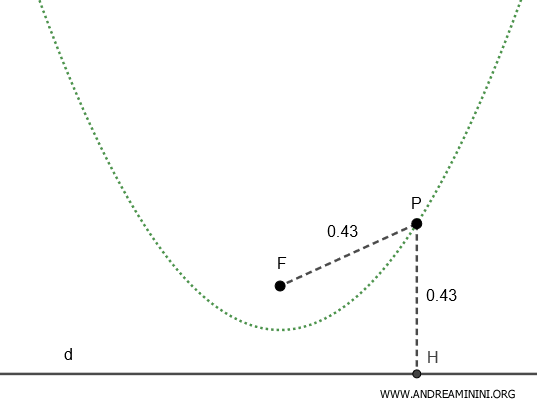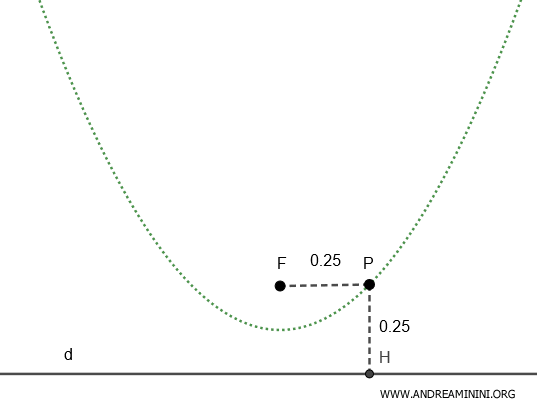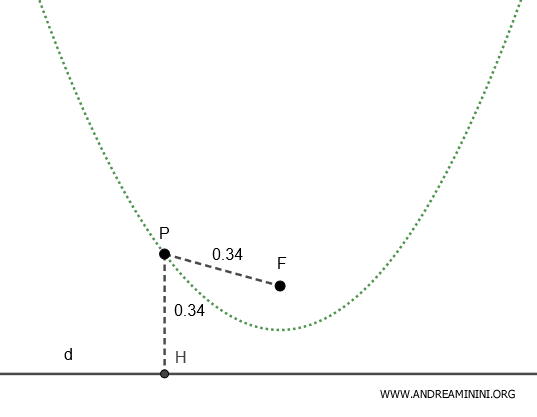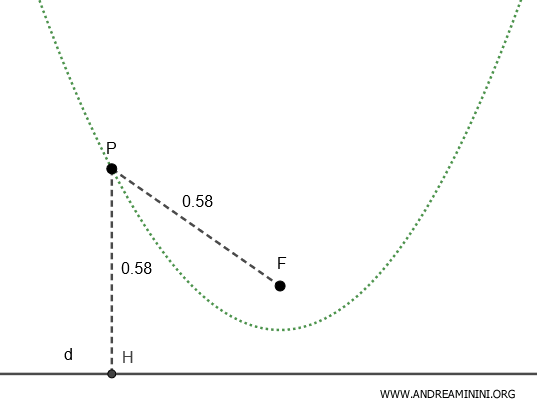
In the case of a parabola, the eccentricity is $ e=1 $.
$$ e = 1 $$
This means the distance PF from any point P on the parabola to the focus F is equal to the distance PH from the same point P to the directrix d.
$$ \frac{ \overline{PF} }{ \overline{PH} } = e = 1 $$
$$ \overline{PF} = \overline{PH} $$
Therefore, the ratio between the two distances $ \frac{ \overline{PF} }{ \overline{PH} } = 1 $ is always equal to one.
Example 2
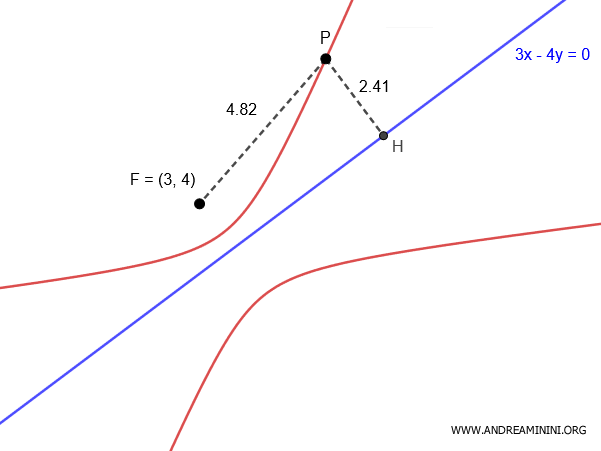
Let's consider a focus at the point $ F(3;4) $ and the line $ 3x-4y=0 $.
We need to find the locus of points $ P(x;y) $ in the plane where the eccentricity is $ e = 2 $.
$$ e = 2 $$
The eccentricity of a conic is the ratio of the distances PF to PH, and it remains constant.
$$ \frac{ \overline{PF} }{ \overline{PH} } = 2 $$
$$ \overline{PF} = 2 \cdot \overline{PH} $$
The Euclidean distance between the points $ P(x;y) $ and $ F(p;q)=(3;4) $ is:
$$ \overline{PF} = \sqrt{(x-p)^2+(y-q)^2} $$
$$ \overline{PF} = \sqrt{(x-3)^2+(y-4)^2} $$
The distance from the point $ P(x;y) $ to the directrix $ 3x-4y=0 $ is:
$$ \overline{PH} = \frac{|3x-4y|}{ \sqrt{3^2+(-4)^2} } $$
$$ \overline{PH} = \frac{|3x-4y|}{ \sqrt{9+16} } $$
$$ \overline{PH} = \frac{|3x-4y|}{ \sqrt{25} } $$
$$ \overline{PH} = \frac{|3x-4y|}{ 5 } $$
Now, substituting these distances into the eccentricity formula:
$$ \overline{PF} = 2 \cdot \overline{PH} $$
$$ \sqrt{(x-3)^2+(y-4)^2} = 2 \cdot \frac{|3x-4y|}{ 5 } $$
We square both sides of the equation:
$$ ( \sqrt{(x-3)^2+(y-4)^2} )^2 = \left( 2 \cdot \frac{|3x-4y|}{ 5 } \right)^2 $$
$$ (x-3)^2+(y-4)^2 = \frac{(|3x-4y|)^2}{ 25 } \cdot 4 $$
$$ (x-3)^2+(y-4)^2 = \frac{(3x-4y)^2}{ 25 } \cdot 4 $$
Expanding the squares gives:
$$ (x^2-6x+9) + (y^2-8y+16) = \frac{ (9x^2-24xy+16y^2)}{ 25 } \cdot 4 $$
$$ x^2 - 6x + 9 + y^2 - 8y + 16 = \frac{36x^2 - 96xy + 64y^2}{25} $$
$$ 25(x^2 - 6x + y^2 - 8y + 25) = 36x^2 - 96xy + 64y^2 $$
$$ 25x^2 - 150x + 25y^2 - 200y + 625 - 36x^2 + 96xy - 64y^2 = 0 $$
$$ (25 - 36)x^2 + 96xy + (25 - 64)y^2 - 150x - 200y + 625 = 0 $$
So, the general equation of the conic is:
$$ -11x^2 + 96xy - 39y^2 - 150x - 200y + 625 = 0 $$
This conic section is characterized by a constant ratio $ \frac{ \overline{PF} }{ \overline{PH} } = 2 $.
General Equation of a Conic
A conic section is described by a second-degree equation of the form $$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$ where the coefficients A, B, C, D, E, F are not all zero at the same time.
For instance, if B=0 and A=0, the equation represents a parabola with its axis parallel to the x-axis.
$$ Cy^2 + Dx + Ey + F = 0 $$
Similarly, if B=0 and C=0, the equation represents a parabola with its axis parallel to the y-axis.
$$ Ax^2 + Dx + Ey + F = 0 $$
When B=0 and A=C with A≠0, the equation describes a circle.
$$ Ax^2 + Cy^2 + Dx + Ey + F = 0 $$
However, if B=0 and A≠C with both A and C non-zero, the equation describes an ellipse if A and C have the same sign (A·C>0), or a hyperbola if they have opposite signs (A·C<0).
$$ Ax^2 + Cy^2 + Dx + Ey + F = 0 $$
Explanation. Let's start by grouping the x and y terms: $$ Ax^2 + Cy^2 + Dx + Ey + F = 0 $$ $$ A ( x^2 + \frac{Dx}{A} ) + C (y^2 + \frac{Ey}{C} ) + F = 0 $$ Next, we'll complete the square: $$ A ( x^2 + \frac{Dx}{A} + ( \frac{D}{2A})^2 - ( \frac{D}{2A})^2 ) + C (y^2 + \frac{Ey}{C} + ( \frac{E}{2C})^2 - ( \frac{E}{2C})^2 ) + F = 0 $$ $$ A ( x^2 + \frac{Dx}{A} + \frac{D^2}{4A^2} - \frac{D^2}{4A^2} ) + C (y^2 + \frac{Ey}{C} + \frac{E^2}{4C^2} - \frac{E^2}{4C^2} ) + F = 0 $$ $$ A ( x^2 + \frac{Dx}{A} + \frac{D^2}{4A^2} ) + C (y^2 + \frac{Ey}{C} + \frac{E^2}{4C^2} ) + F - \frac{D^2}{4A} - \frac{E^2}{4C} = 0 $$ $$ A ( x + \frac{D}{2A} )^2 + C (y + \frac{E}{2C} )^2 + F - \frac{D^2}{4A} - \frac{E^2}{4C} = 0 $$ $$ A ( x + \frac{D}{2A} )^2 + C (y + \frac{E}{2C} )^2 = \frac{D^2}{4A} + \frac{E^2}{4C} - F $$ We can simplify this by introducing 's': $$ A ( x + \frac{D}{2A} )^2 + C (y + \frac{E}{2C} )^2 = s $$ This also represents the reality condition for an ellipse or a hyperbola where $ s > 0 $ $$ s = \frac{D^2}{4A} + \frac{E^2}{4C} - F $$ because an ellipse only exists if $ s > 0 $. If $ s = 0 $, the ellipse collapses into a single point, while if $ s < 0 $, the ellipse does not exist. For a hyperbola, the term 's' can be positive or negative depending on whether the hyperbola's axis is parallel to the x-axis or y-axis, but it cannot be zero. If $ s = 0 $, the hyperbola degenerates into a pair of intersecting lines. Returning to the equation: $$ A ( x + \frac{D}{2A} )^2 + C (y + \frac{E}{2C} )^2 = s $$ we can interpret this as a translation of the conic from the origin of the Cartesian plane (0,0) by a vector $ \left( - \frac{D}{2A}; - \frac{E}{2C} \right) $, which represents the center of the conic, giving us the canonical form: $$ Ax^2 + Cy^2= s $$ Depending on the sign of A and C, this represents either an ellipse or a hyperbola.
Example
Let's consider the following second-degree equation:
$$ -2x^2 + y^2 - 6x - 5y + 3 = 0 $$
We need to determine whether this represents a conic section.
In this case, A=-2, B=0, C=1, D=-6, E=-5, F=3
Since B=0 and A≠C with A≠0 and C≠0, we can infer that this might be a hyperbola because A and C have opposite signs (A·C<0), indicating they are discordant.
Let's apply the method of completing the square:
$$ (-2x^2 - 6x) + (y^2 - 5y) + 3 = 0 $$
$$ -2(x^2 + 3x) + (y^2 - 5y) + 3 = 0 $$
$$ -2(x^2 + 3x + (\frac{3}{2} )^2 - (\frac{3}{2} )^2) + (y^2 - 5y + (\frac{5}{2} )^2 - (\frac{5}{2} )^2) + 3 = 0 $$
$$ -2(x^2 + 3x + (\frac{3}{2} )^2 ) + (y^2 - 5y + (\frac{5}{2} )^2 ) + 3 - (\frac{3}{2} )^2 \cdot (-2) - (\frac{5}{2} )^2 = 0 $$
$$ -2(x + \frac{3}{2} )^2 + (y - \frac{5}{2} )^2 + 3 - \frac{9}{4} \cdot (-2) - \frac{25}{4}= 0 $$
$$ -2(x + \frac{3}{2} )^2 + (y - \frac{5}{2} )^2 + 3 + \frac{9}{2} - \frac{25}{4}= 0 $$
$$ -2(x + \frac{3}{2} )^2 + (y - \frac{5}{2} )^2 + \frac{12 + 18 - 25}{4} = 0 $$
$$ -2(x + \frac{3}{2} )^2 + (y - \frac{5}{2} )^2 + \frac{5}{4}= 0 $$
$$ -2(x + \frac{3}{2} )^2 + (y - \frac{5}{2} )^2 = - \frac{5}{4} $$
We can convert this to the canonical form of a hyperbola by multiplying both sides by -1:
$$ (-1) \cdot [ -2(x + \frac{3}{2} )^2 + (y - \frac{5}{2} )^2 ] = (-1) \cdot ( - \frac{5}{4} ) $$
$$ 2(x + \frac{3}{2} )^2 - (y - \frac{5}{2} )^2 = \frac{5}{4} $$
This final equation represents a hyperbola centered at $ \left( - \frac{3}{2}; \frac{5}{2} \right) $ with its transverse axis, which contains the foci, parallel to the x-axis.
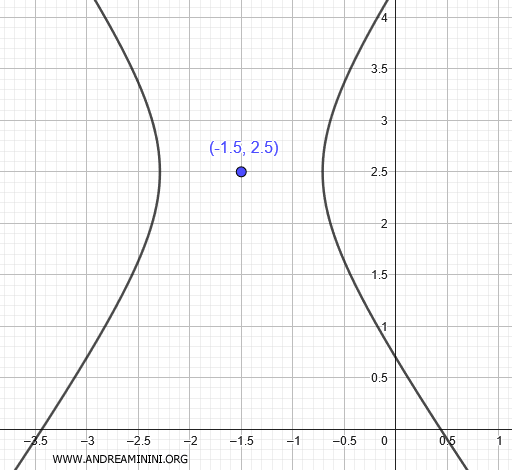
Example 2
Let's examine another second-degree equation:
$$ 4x^2 + 9y^2 - 5x - y + 10 = 0 $$
We need to determine whether this is a conic section.
In this case, A=4, B=0, C=9, D=-5, E=-1, F=10
Since B=0 and A≠C with both A and C non-zero, we can infer that this might be an ellipse because A and C are concordant (A·C>0), meaning they have the same sign.
Let's group the x and y terms:
$$ (4x^2 - 5x) + (9y^2 - y) + 10 = 0 $$
Next, we'll complete the square:
$$ (4x^2 - 5x + (\frac{5}{4})^2 - (\frac{5}{4})^2 ) + (9y^2 - y + (\frac{1}{6})^2 - (\frac{1}{6})^2) + 10 = 0 $$
$$ (4x^2 - 5x + (\frac{5}{4})^2 ) + (9y^2 - y + (\frac{1}{6})^2) + 10 - (\frac{5}{4})^2 - (\frac{1}{6})^2 = 0 $$
$$ (2x - \frac{5}{4})^2 + (3y - \frac{1}{6})^2 + 10 - \frac{25}{16} - \frac{1}{36} = 0 $$
$$ (2x - \frac{5}{4})^2 + (3y - \frac{1}{6})^2 + \frac{1440 - 225 - 4}{144} = 0 $$
$$ (2x - \frac{5}{4})^2 + (3y - \frac{1}{6})^2 + \frac{1211}{144} = 0 $$
$$ (2x - \frac{5}{4})^2 + (3y - \frac{1}{6})^2 = - \frac{1211}{144} $$
In this case, however, the condition for the existence of an ellipse is not satisfied because the constant term on the right side is negative:
$$ s = - \frac{1211}{144} < 0 $$
Thus, this equation does not represent a conic section.
Proof
Let's consider a directrix line given by \( ax + by + c = 0 \) and a generic point \( P(x; y) \) on the conic that doesn’t lie on this line.
By definition, a conic is the set of all points \( P(x, y) \) such that the ratio of the distance from \( P \) to a fixed point \( F \) (the focus) to the distance from \( P \) to a fixed line \( d \) (the directrix) is constant, known as the eccentricity \( e \):
$$ \frac{ \overline{PF} }{ \overline{PH} } = e $$
$$ \overline{PF} = \overline{PH} \cdot e $$
The distance \( PF \) between the point \( P(x;y) \) and the focus \( F(p;q) \) of the conic is given by:
$$ \overline{PF} = \sqrt{(x-p)^2 + (y-q)^2} $$
The distance \( PH \) between the point \( P(x;y) \) and the directrix \( ax+by+c=0 \), where \( x \) and \( y \) are the coordinates of \( P \), is given by:
$$ \overline{PH} = \frac{|ax+by+c|}{ \sqrt{a^2 + b^2} } $$
Substituting these distance expressions, we get:
$$ \overline{PF} = \overline{PH} \cdot e $$
$$ \sqrt{(x-p)^2 + (y-q)^2} = \frac{|ax+by+c|}{ \sqrt{a^2 + b^2} } \cdot e $$
Squaring both sides of the equation gives us:
$$ \left( \sqrt{(x-p)^2 + (y-q)^2} \right)^2 = \left( \frac{|ax+by+c|}{ \sqrt{a^2 + b^2} } \cdot e \right)^2 $$
$$ (x-p)^2 + (y-q)^2 = \frac{(|ax+by+c|)^2}{a^2 + b^2} \cdot e^2 $$
Expanding the squares and rearranging terms, we have:
$$ (x^2 - 2xp + p^2) + (y^2 - 2yq + q^2) = \frac{e^2}{a^2 + b^2} \cdot (a^2x^2 + 2abxy + b^2y^2 + 2acx + 2bcy + c^2) $$
Grouping the like terms and bringing everything to one side, we arrive at the general form:
$$ [(1-e^2)a^2 + b^2]x^2 + 2abe^2xy + [(1-e^2)b^2 + a^2]y^2 \\ - 2(a^2p + b^2p + ace)x - 2(a^2q + b^2q + bce)y \\ + (p^2 + q^2)(a^2 + b^2) - c^2e^2 = 0 $$
This expression can be rewritten in the standard form of a conic equation:
$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$
where the coefficients \( A \), \( B \), \( C \), \( D \), \( E \), and \( F \) are defined in terms of \( a \), \( b \), \( c \), \( p \), \( q \), and \( e \).
- $ A = (1-e^2)a^2 + b^2 $
- $ B = 2abe^2 $
- $ C = (1-e^2)b^2 + a^2 $
- $ D = -2(a^2p + b^2p + ace) $
- $ E = -2(a^2q + b^2q + bce) $
- $ F = (p^2 + q^2)(a^2 + b^2) - c^2e^2 $
This equation represents a conic, which can be an ellipse, a parabola, or a hyperbola depending on the value of the eccentricity \( e \).
- If \( e = 0 \), the conic is a circle.
- If \( 0 < e < 1 \), the conic is an ellipse.
- If \( e = 1 \), the conic is a parabola.
- If \( e > 1 \), the conic is a hyperbola.
Thus, starting from the definition of a conic and the distance formulas, we have derived the general equation of a conic in the Cartesian plane.
Imaginary and Degenerate Conics
The general second-degree equation \[ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0, \qquad (A,B,C \ \text{not all zero}) \] is classified according to the discriminant \(\Delta = B^2 - 4AC\).
This discriminant separates conics into three main families:
- if \(\Delta < 0\), the curve is elliptic (ellipse or circle);
- if \(\Delta = 0\), the curve is parabolic (parabola);
- if \(\Delta > 0\), the curve is hyperbolic (hyperbola).
Yet the discriminant by itself is not sufficient. It does not ensure that the equation has real solutions, nor does it rule out degenerate cases.
In other words, the discriminant only indicates the family to which the equation belongs (elliptic, parabolic, hyperbolic). It does not reveal whether the conic is imaginary (with no real points on the Cartesian plane) or whether it degenerates into straight lines.
For example, with \(\Delta < 0\) one may obtain either a real ellipse or an imaginary ellipse (with no real points). With \(\Delta = 0\) one may find not only a parabola but also a pair of parallel lines. With \(\Delta > 0\) a hyperbola can reduce to two intersecting real lines.
To detect degenerate cases, one examines the symmetric matrix associated with the equation:
\[ Q = \begin{pmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{pmatrix}. \]
Its determinant is the invariant that distinguishes proper conics from degenerate ones:
- if \(\det(Q) \neq 0\), the curve is a real, non-degenerate conic (ellipse, parabola, or hyperbola);
- if \(\det(Q) = 0\), the equation represents a degenerate conic, i.e. a configuration of lines (intersecting, parallel, or imaginary, depending on the sign of \(\Delta\)).
The determinant of the symmetric matrix indicates whether the conic degenerates (into a pair of real, parallel, or imaginary lines) or not.
Note. The determinant of (Q) only shows whether the conic is degenerate or non-degenerate; it does not guarantee the presence of real points. Even with \( \det(Q) \neq 0 \), the conic may still be imaginary-an equation with no real solutions (such as \(x^2 + y^2 + 1 = 0\)) and therefore invisible on the Cartesian plane. To determine whether the conic can actually be drawn, one must check whether the equation admits real solutions, i.e. whether there exist real values of (x) and (y) that satisfy it.
Examples of Conic Classification
Example 1 (real ellipse)
Consider the equation
\[ x^2 + 2y^2 - 4 = 0 \]
Here \(A=1\), \(B=0\), \(C=2\). The discriminant is
$$ \Delta = 0^2 - 4\cdot 1 \cdot 2 = -8 < 0 $$
Thus the conic is elliptic. The equation has real solutions and represents a real ellipse with semi-axes \(\sqrt{4}\) and \(\sqrt{2}\).
Example 2 (imaginary ellipse, no real points)
Now take the equation
\[ x^2 + y^2 + 1 = 0 \]
Here \(A=1\), \(B=0\), \(C=1\). The discriminant is
$$ \Delta = 0 - 4 \cdot 1 \cdot 1 = -4 < 0 $$
The curve is elliptic, but the equation has no real solutions: this is an imaginary ellipse.
What is an imaginary conic? In plain terms, an imaginary conic is a curve that “exists” algebraically as an equation but does not appear on the Cartesian plane, since there are no real points to plot. It is therefore an algebraic object only, not a geometric one.
Example 3 (parabola)
Take the equation
\[ y - x^2 = 0 \]
Here \(A=1\), \(B=0\), \(C=0\). The discriminant is
$$ \Delta = 0^2 - 4\cdot 1 \cdot 0 = 0 $$
Thus the conic is parabolic. The equation represents a parabola with vertical axis.
Example 4 (pair of parallel lines)
Consider the equation
\[ x^2 - 1 = 0 \]
The coefficients are \(A=1\), \(B=0\), \(C=0\), \(D=0\), \(E=0\), \(F=-1\). The discriminant is
\[ \Delta = B^2 - 4AC = 0^2 - 4 \cdot 1 \cdot 0 = 0 \]
Thus the curve is parabolic.
To analyze further, the associated matrix \(Q\) is
\[ Q = \begin{pmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{pmatrix} \]
The determinant is
\[ \det(Q) = \begin{vmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{vmatrix} = 1 \cdot (0 \cdot -1 - 0 \cdot 0) = 0 \]
Since \(\det(Q) = 0\), the conic is degenerate. In fact, the equation factors as
\[ x^2 - 1 = (x-1)(x+1) = 0 \]
The curve is not a parabola but a pair of vertical parallel lines \(x=1\) and \(x=-1\).
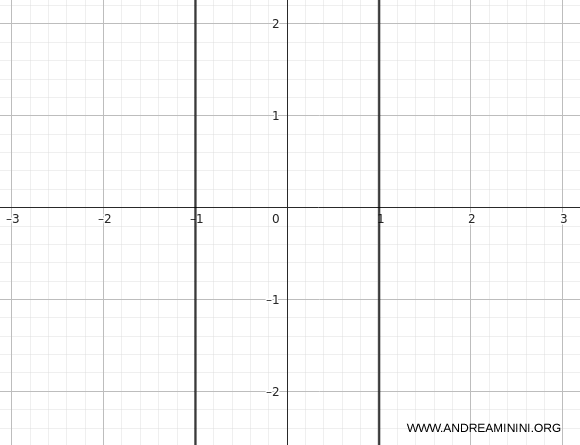
Example 5 (hyperbola)
Consider the equation
\[ x^2 - y^2 - 1 = 0 \]
Here \(A=1\), \(B=0\), \(C=-1\). The discriminant is \(\Delta = 0 - 4\cdot 1 \cdot (-1) = 4 > 0\), so the curve is hyperbolic.
The equation represents a hyperbola with asymptotes \(y = \pm x\).
Example 6 (pair of intersecting real lines)
Consider the equation
\[ x^2 - y^2 = 0 \]
The coefficients are \(A=1\), \(B=0\), \(C=-1\), \(D=0\), \(E=0\), \(F=0\).
The discriminant is
\[ \Delta = B^2 - 4AC = 0^2 - 4 \cdot 1 \cdot (-1) = 4 > 0 \]
Thus the curve is hyperbolic.
The associated matrix is
\[ Q = \begin{pmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{pmatrix} \]
The determinant is zero:
\[ \det(Q) = \begin{vmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{vmatrix} = 1 \cdot (-1) \cdot 0 = 0 \]
Since \(\det(Q) = 0\), the conic degenerates into two lines. Indeed, the equation factors as
\[ x^2 - y^2 = (x-y)(x+y) = 0 \]
The curve is not a true hyperbola but a pair of intersecting real lines \(y=x\) and \(y=-x\).
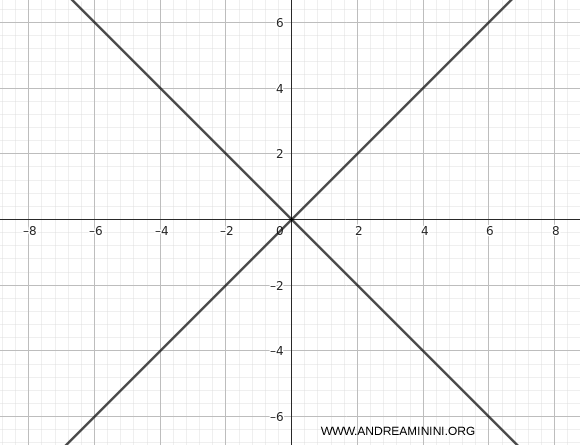
Additional Notes
Some further remarks on conic sections.
- Removing the mixed xy term from a conic equation
The mixed $ xy $ term in a conic equation can be eliminated by rotating the coordinate axes through an angle $ \alpha $ that satisfies $$ \tan 2 \alpha = \frac{B}{A-C} $$ where $ A, B, C $ are the coefficients in the general equation of the conic.Note. If the denominator $ A-C=0 $, then $\tan 2\alpha$ is undefined because the angle is vertical. In this special case, the condition reduces to $\cos 2\alpha = 0$, which implies $2\alpha = \pi/2 + k\pi$.
And so forth...
