Hyperbola
A hyperbola is a plane curve where the absolute difference in distances from any point P to two fixed points, F1 and F2, known as the foci, is constant (2a). $$ | \overline{PF}_1 - \overline{PF}_2 | = 2a $$ where 2a is the distance between the two vertices of the hyperbola.
A hyperbola is an open curve divided into two branches that extend to infinity along the direction of two oblique lines called asymptotes.
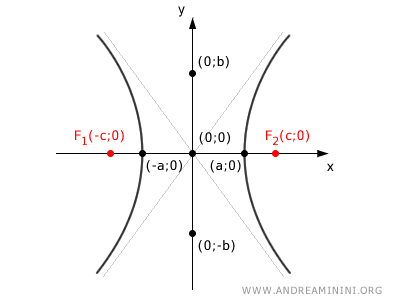
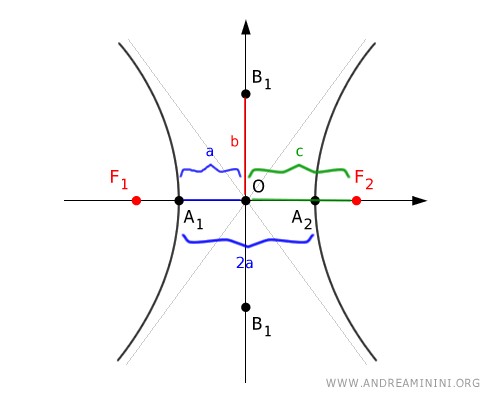
The two vertices (-a;0) and (a;0) of the hyperbola are separated by a distance of 2a.
The distance from each vertex to the center of the hyperbola is "a".
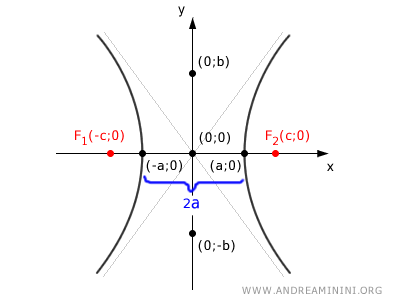
If you take any two points P1 and P2 on the hyperbola, the absolute difference in their distances from the foci is always the same.
In other words, any pair of points on the hyperbola satisfies this relationship:
$$ | \overline{P_1F_1} - \overline{P_1F_2} | = | \overline{P_2F_1} - \overline{P_2F_2} | $$
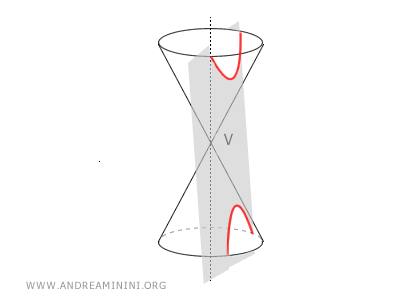
Note: The hyperbola is a conic section because it can be obtained by intersecting a circular cone with a plane that has an angle less than the cone's opening angle.
Characteristics
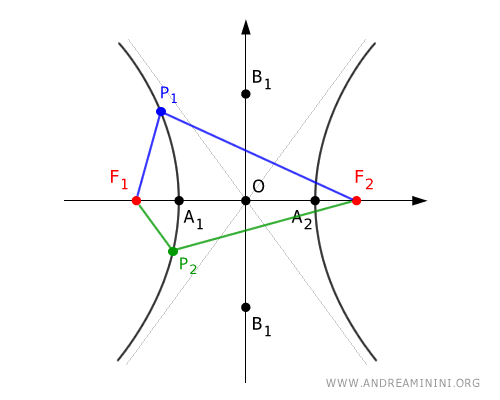
A hyperbola is a geometric locus where the points in the plane maintain a constant difference in their distances from two fixed points, F1 and F2, called foci.
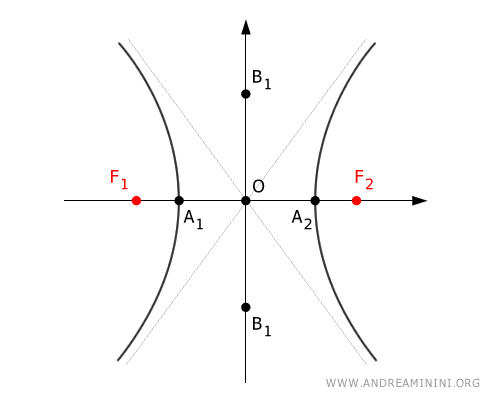
The line passing through the foci F1 and F2 is called the principal axis (or transverse axis).
The intersection points A1 and A2 of the hyperbola with the principal axis are called real vertices.
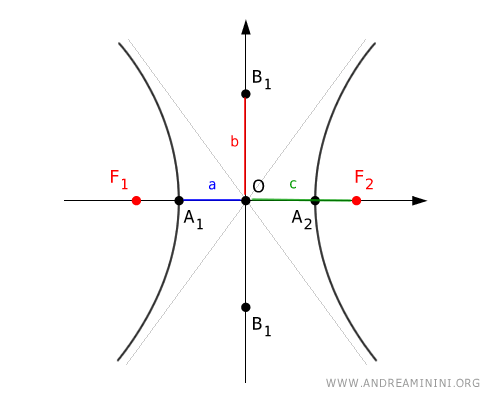
Note: In some texts, the "transverse axis" also refers to the segment between the real vertices A1 and A2, which is always equal to 2a. $$ \overline{A_1A_2} = 2a $$ In these cases, the semi-transverse axis refers to the distance "a" between a vertex and the center O of the hyperbola. $$ \overline{OA_1} = \overline{OA_2} = a $$
The segment F1F2 is called the secondary axis (or conjugate axis).
The two points B1 and B2 on the secondary axis are called imaginary vertices, as they do not intersect the hyperbola but help determine the slope of the asymptotes.
The intersection point O of the two axes, principal and secondary, is called the center of the hyperbola.
It is the midpoint $ O $ of the segment \overline{F_1F_2} between the two foci.
In the diagram, the terms "a", "b", and "c" respectively indicate the distances from the center O to the real vertices, imaginary vertices, and the foci.
The asymptotes are the oblique lines passing through the center O of the hyperbola and are tangent to the curve at infinity.
The distance between the two foci $ F_1 $ and $ F_2 $ is called the focal distance.
$$ 2c = \overline{F_1F_2} $$
Given a point $ P $ on the hyperbola, the absolute difference in the segments $ | \overline{PF}_1 - \overline{PF}_2 | $ is constant and equals $ 2a $
$$ | \overline{PF}_1 - \overline{PF}_2 | = 2a $$
Point $ P $ and the foci $ F_1 $ and $ F_2 $ form a triangle $ PF_1F_2 $ where the longest side is always $ \overline{F_1F_2} = 2c $.
The difference of the other two sides of the triangle is $ | \overline{PF}_1 - \overline{PF}_2 | = 2a $
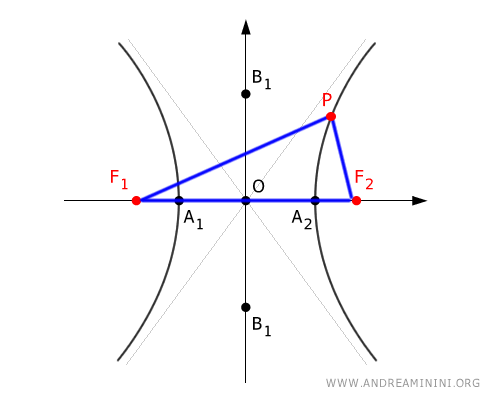
According to the triangle inequality theorem, in a triangle, one side is always greater than the difference of the other two sides, hence 2c>2a
$$ 2c > 2a $$
therefore
$$ c > a $$
Thus, in a hyperbola, the distance $ c $ from a focus to the center $ O $ is always greater than the distance from a vertex to the center.
The Canonical Equation of the Hyperbola
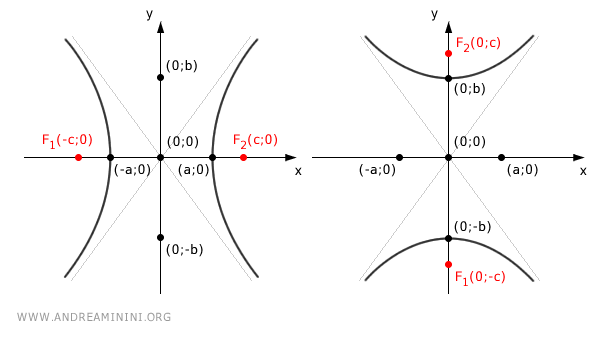
To represent a hyperbola, it is common to use a Cartesian coordinate system where:
- the center of the hyperbola is at the origin O(0;0)
- the principal axis of the hyperbola, which passes through the foci F1 and F2, coincides with either the x-axis or the y-axis.
This simplification allows us to use the canonical equation of the hyperbola.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$
Where "a" and "b" are the semi-distances between the vertices of the hyperbola.
- If the principal axis is the x-axis, the canonical equation's constant term is +1 $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
- If the principal axis is the y-axis, the canonical equation's constant term is -1 $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
In other words, depending on whether the foci F1 and F2 are on the x-axis or y-axis, the constant term of the hyperbola's canonical equation is either +1 or -1.
Alternatively, you can also use the explicit form of the hyperbola's equation.
$$ y = \pm \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}-1 ) } \ \ \ \ \text{foci on the x-axis}$$
$$ y = \pm \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}+1 ) } \ \ \ \ \text{foci on the y-axis}$$
Depending on the choice of the principal axis, the foci of the hyperbola are located at the following coordinates:
- If the principal axis is the x-axis $$ F_1(-c;0 ) $$ $$ F_2(c;0 ) $$
- If the principal axis is the y-axis $$ F_1(0;-c ) $$ $$ F_2(0;c ) $$
Where "c" is the distance of the foci from the center of the hyperbola.
$$ c = \sqrt{a^2+b^2} $$
Note: If the principal axis is the x-axis, the value "c" is always greater than "a" (c>a). Conversely, if the principal axis is the y-axis, the value "c" is always greater than "b" (c>b).
The asymptotes of the hyperbola are the lines defined by the following equations:
$$ y = \pm \frac{b}{a} x $$
In this simplified case, the hyperbola's asymptotes always pass through the origin O(0;0) of the Cartesian axes and through the points (a;b) or (a;-b).
Finally, the eccentricity (e) of the hyperbola is measured by the ratio of the distance of the foci (c) to the real vertices (a) from the center.
$$ e = \frac{c}{a} $$
The higher the value of "e", the more open the branches of the hyperbola are.
Note: Unlike an ellipse, the eccentricity of a hyperbola is always greater than 1, i.e., e>1, because the distance of the foci from the center is always greater than the distance of the vertices.
Every hyperbola has two foci and two directrix lines that are symmetrical and perpendicular to the transverse axis.
If the transverse axis is along the x-axis, the directrix lines are given by:
$$ x = \pm \frac{a^2}{c} $$
If the transverse axis is along the y-axis, the directrix lines are:
$$ y = \pm \frac{b^2}{c} $$
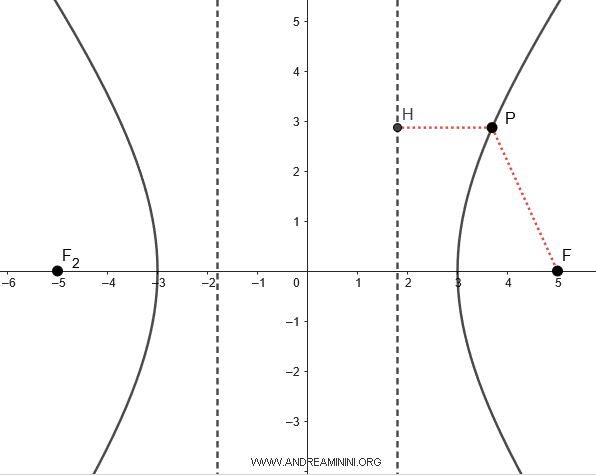
In general, as with any conic section, for a given point $ P(x;y) $ on the hyperbola, the ratio between the distance $ \overline{PF} $ from the point to the focus and the distance $ \overline{PH} $ from the point to the directrix is constant and equal to the eccentricity (e).
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
A Practical Example
Consider a hyperbola with its foci on the x-axis, its center at the origin of the Cartesian axes O(0;0), and with a=3 and b=4.
First, identify the points (a;b)=(3;4) and (a;-b)=(3;-4).
Then draw the lines passing through the center of the hyperbola and the two points (3;4) and (3;-4).
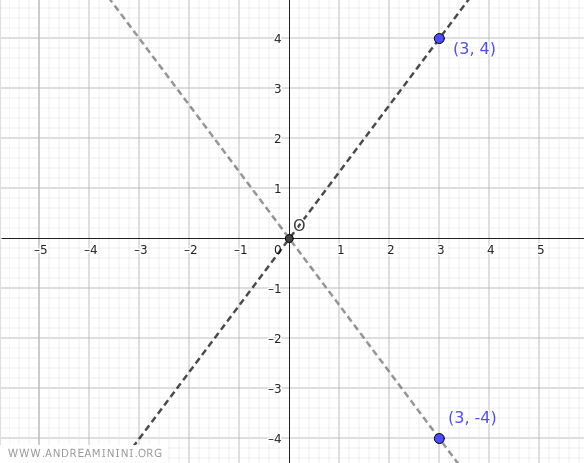
In this way, you obtain the asymptotes of the hyperbola.
To find the asymptotes, you could also use the explicit equation:
$$ y = \pm \frac{b}{a} \cdot x $$
Substitute a=3 and b=4:
$$ y = \pm \frac{4}{3} \cdot x $$
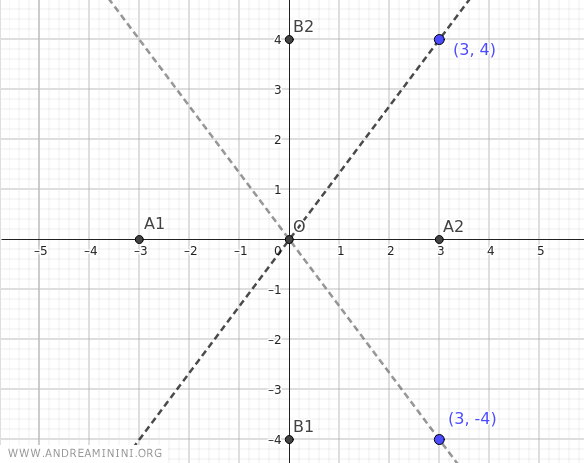
Once the asymptotes are drawn, find the vertices of the hyperbola.
In this case, the foci are on the x-axis, so the real vertices of the hyperbola are A1(-a;0) and A2(a;0), and the imaginary vertices are B1(0;-b) and B2(0;b).
Knowing that a=3 and b=4, the real vertices are located at A1(-3;0) and A2(3;0), while the imaginary vertices are at B1(0;-4) and B2(0;4).
Next, calculate the coordinates (x;y) of the foci of the hyperbola.
The foci are located at a distance "c" from the center of the hyperbola, which is found using this formula:
$$ c = \sqrt{a^2+b^2} $$
Substitute a=3 and b=4:
$$ c = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5 $$
Since the principal axis is the x-axis, the foci are located at F1(-c;0) and F2(c;0) where c=5:
$$ F_1(-5;0) $$
$$ F_2(5;0) $$
Add the two foci F1(-5;0) and F2(5;0) to the Cartesian plane.
Finally, find other points on the hyperbola using the canonical equation of the hyperbola.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
In this case, the constant term of the equation is +1 because the foci of the hyperbola are on the x-axis.
Solve for y in terms of the other variables:
$$ - \frac{y^2}{b^2} = 1 - \frac{x^2}{a^2} $$
$$ - y^2 = b^2 \cdot ( 1 - \frac{x^2}{a^2}) $$
Multiply both sides of the equation by -1 to get a positive y:
$$ - y^2 \cdot (-1) = b^2 \cdot ( 1 - \frac{x^2}{a^2}) \cdot (-1) $$
$$ y^2 = - b^2 \cdot ( 1 - \frac{x^2}{a^2}) $$
$$ y^2 = b^2 \cdot ( \frac{x^2}{a^2}-1) $$
Take the square root of both sides of the equation:
$$ \sqrt{ y^2 } = \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}-1) } $$
$$ y = \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}-1 ) } $$
Substitute the parameters a=3 and b=4 for the hyperbola:
$$ y = \sqrt{ 4^2 \cdot ( \frac{x^2}{3^2}-1 ) } $$
$$ y = \sqrt{ 16 \cdot ( \frac{x^2}{9}-1 ) } $$
In this way, you can find the y-coordinate of any point (x;y) starting from the x-coordinate in the interval (-∞,-a]∪[a,∞), i.e., (-∞,-3]∪[3,∞).
| x | y |
|---|---|
| -5 | ±5.33 |
| -4 | ±3.53 |
| -3 | 0 |
| 3 | 0 |
| 4 | ±3.53 |
| 5 | ±5.33 |
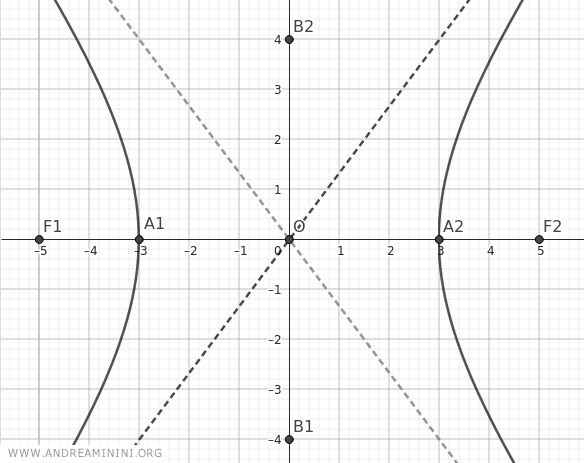
These points already give an approximate idea of the shape of the hyperbola.
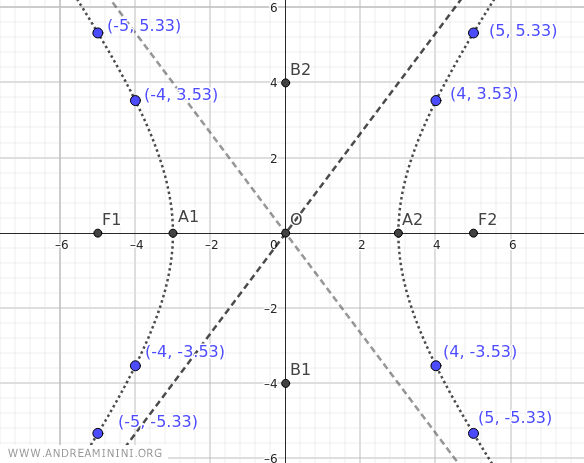
To make the graph more precise, calculate the coordinates of additional points.
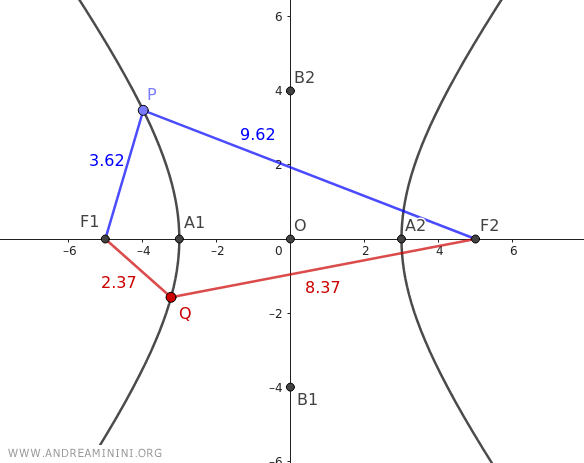
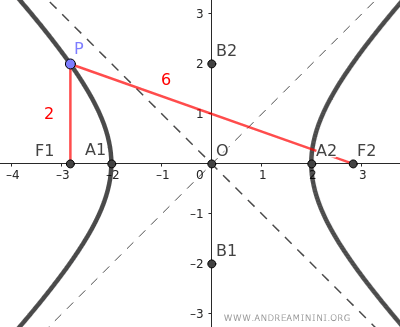
Note: As mentioned earlier, a hyperbola is a geometric locus where every point has the same absolute difference in distances from the foci. At this point, you can verify this property. Consider two points P and Q on the hyperbola and calculate their respective distances from the foci. Point P (blue) is 3.62 from F1 and 9.62 from F2. Thus, the absolute difference in distances is |9.62-3.62|=6. Point Q (red) is 2.37 from F1 and 8.37 from F2. Again, the absolute difference in distances is 6 because |8.37-2.37|=6. This holds for any other point on the hyperbola.
In this case, the hyperbola's transverse axis coincides with the x-axis, so the directrix lines are:
$$ x = \pm \frac{a^2}{c} = \pm \frac{9}{5} $$
The ratio between the distance $ \overline{PF} $ from a point $ P(x;y) $ to the focus $ F(c,0) $ of the hyperbola and the distance $ \overline{PH} $ from the same point $ P $ to the directrix is constant and equal to the eccentricity (e) of the hyperbola.
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
For example, in the specific case of point $ P $, the segments have lengths $ \overline{PF} = 3.15 $ and $ \overline{PH} = 1.89 $
$$ e = \frac{ \overline{PF} }{ \overline{PH} } = \frac{3.15}{1.89} = 1.67 $$
This ratio $ e=1.67 $ remains constant for any other point on the hyperbola.
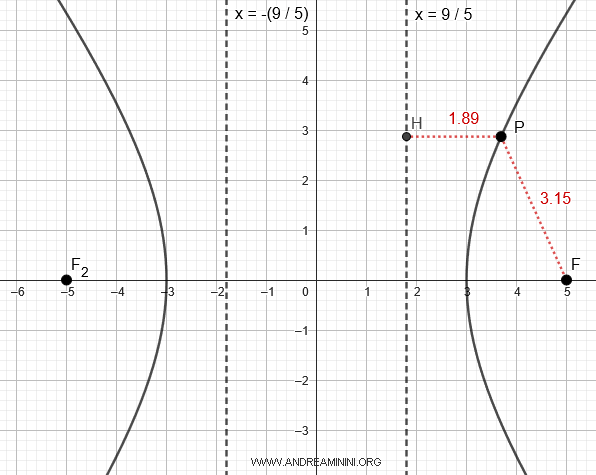
Note: Another way to calculate the eccentricity of the hyperbola is with the formula $$ e = \frac{c}{a} $$ In this case, with $ c=5 $ and $ a=3 $, we have $$ e = \frac{c}{a} = \frac{5}{3} = 1.67 $$ The final result is the same.
Example 2
In this example, we calculate the hyperbola with its foci on the y-axis and its center at the origin of the Cartesian axes O(0;0), using the same parameters a=3 and b=4 as in the previous example.
The asymptotes are the lines that pass through the origin and the points (a;b) or (a;-b), i.e., (3;4) or (3;-4).
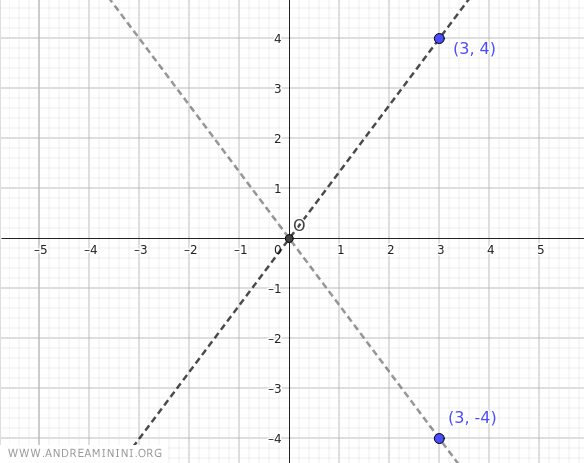
As you can see, the asymptotes are the same.
The vertices of the hyperbola are also the same, but in this case, the real vertices are B1(0;-b) and B2(0;b), while the imaginary vertices are A1(-a;0) and A2(a;0).
In other words, in this case, the curve of the hyperbola passes through points B1 and B2.
Knowing that a=3 and b=4, the real vertices are located at B1(0;-4) and B2(0;4), while the imaginary vertices are at A1(-3;0) and A2(3;0).
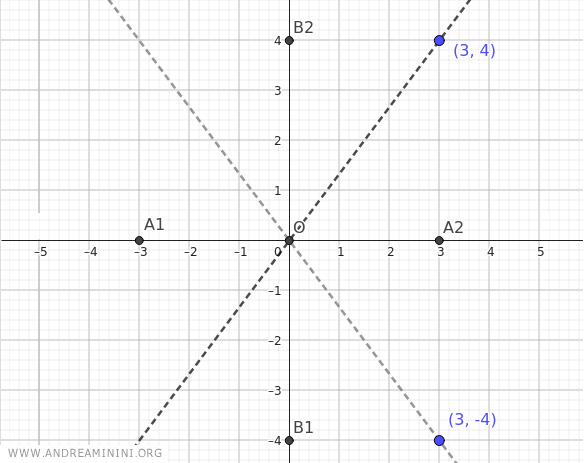
The foci of the hyperbola are always at a distance "c" from the center of the hyperbola.
The formula to calculate the distance is the same:
$$ c = \sqrt{a^2+b^2} $$
Substitute a=3 and b=4:
$$ c = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5 $$
In this case, however, the principal axis is the y-axis.
Therefore, the coordinates of the foci are different from the previous example. They are F1(0;-c) and F2(0;c) with c=5:
$$ F_1(0;-5) $$
$$ F_2(0;5) $$
Add the two foci F1(0;-5) and F2(0;5) to the graph.
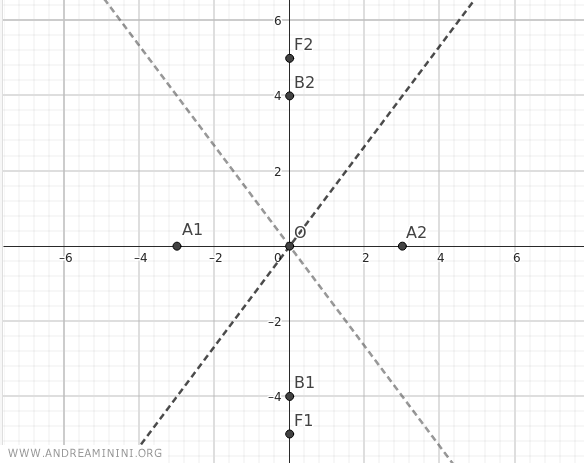
Now, find the various points on the hyperbola using the canonical equation of the hyperbola.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
In this case, the constant term of the equation is -1 because the foci of the hyperbola are on the y-axis.
Solve for y in terms of the other variables:
$$ y = \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}+1 ) } $$
Substitute a=3 and b=4:
$$ y = \sqrt{ 4^2 \cdot ( \frac{x^2}{3^2}+1 ) } $$
$$ y = \sqrt{ 16 \cdot ( \frac{x^2}{9}+1 ) } $$
Use this to find the coordinates (x;y) of some points in the interval (-∞,∞).
| x | y |
|---|---|
| -2 | ±4.81 |
| -1 | ±4.22 |
| 0 | 0 |
| 1 | ±4.22 |
| 2 | ±4.81 |
| 3 | ±5.66 |
These initial coordinates (x;y) already give an idea of the shape of the hyperbola.
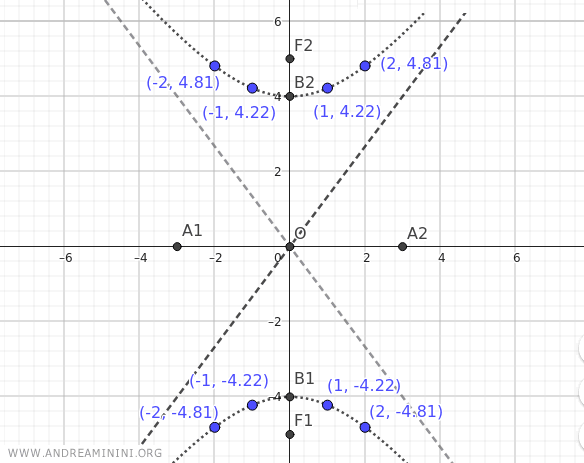
The final result is a hyperbola with its foci on the y-axis.
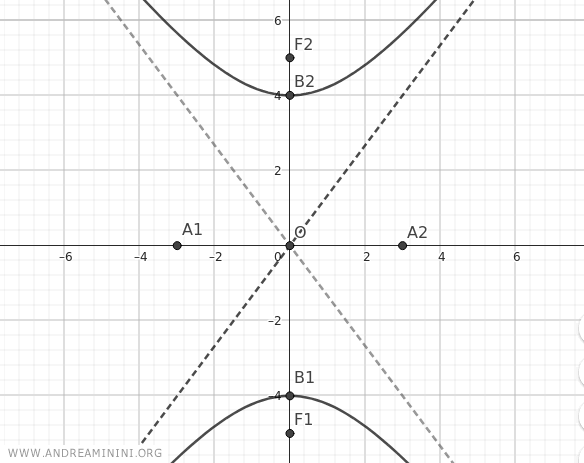
In this scenario, the transverse axis, which contains the foci, coincides with the y-axis.
Therefore, the directrix lines are perpendicular to the y-axis.
$$ y = \pm \frac{b^2}{c} = \frac{16}{5} = 3.2 $$
Here too, the ratio between the distances $ \overline{PF} $ and $ \overline{PH} $ is constant and equal to the eccentricity (e) of the hyperbola.
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
For instance, in the specific case of point $ P $, the segments measure $ \overline{PF} = 3.69 $ and $ \overline{PH} = 2.95 $
$$ e = \frac{ \overline{PF} }{ \overline{PH} } = \frac{3.69}{2.95} = 1.25 $$
This ratio $ e=1.25 $ represents the eccentricity of the hyperbola and remains constant for any point on the hyperbola.
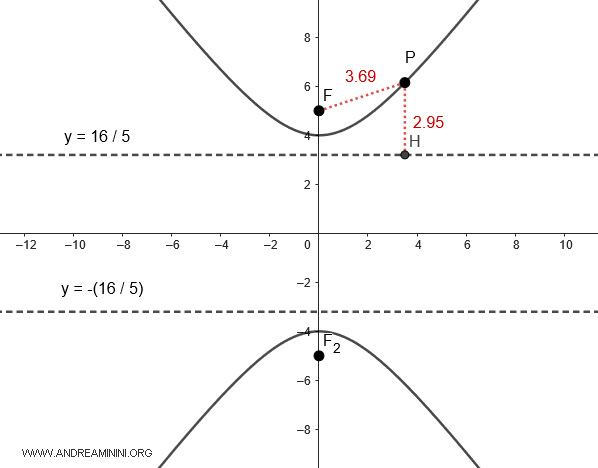
Note: Another way to calculate the eccentricity of the hyperbola when its focal axis is along the y-axis is with the following formula $$ e = \frac{c}{b} = \frac{5}{4} = 1.25 $$ The final result is always the same.
Notes
Some observations and additional notes on the hyperbola:
- Equilateral Hyperbola
The equilateral hyperbola is a special case where a=b. In the equilateral hyperbola, the real vertices on the transverse axis (A1, A2) and the imaginary vertices on the conjugate axis (B1, B2) are equidistant from the center of the hyperbola.
- A line intersects a hyperbola at no more than two real points
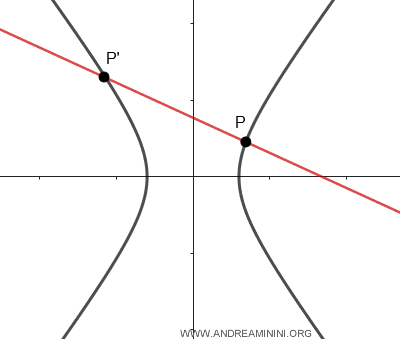
- If a line intersects the hyperbola at two distinct points, it’s called a secant line to the hyperbola.
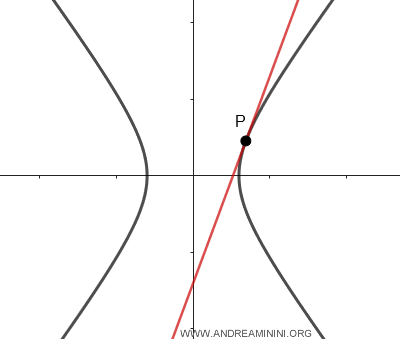
- If the line intersects the hyperbola at just one point, it’s called a tangent line to the hyperbola.
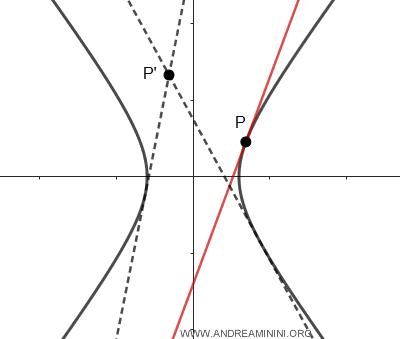
Note. At any point P' on the plane, there can be at most two tangent lines to the hyperbola. However, at a point P on the hyperbola itself, there is only one tangent line.
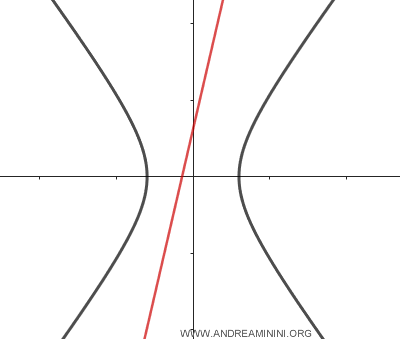
- If a line doesn’t intersect the hyperbola at all, it’s called an external line to the hyperbola.
- If a line intersects the hyperbola at two distinct points, it’s called a secant line to the hyperbola.
- The focal property of the hyperbola
In a hyperbola, if you draw a tangent (t) at a point \( P \) on the curve, the perpendicular (n) to this tangent at point \( P \) bisects the angle formed by the focal radius \( PF_1 \) and the extension of the other focal radius \( PF_2 \), creating two congruent angles \( \alpha \cong \beta \).
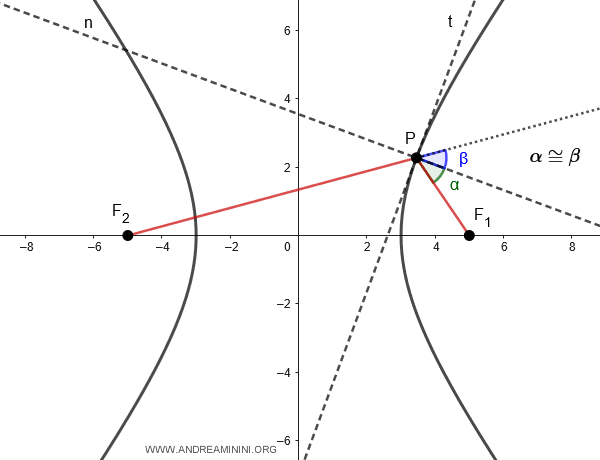
This means that if one focus is the source of a light ray (e.g., F1), the ray is reflected by the hyperbolic mirror as if it were coming from the other focus (e.g., F2).
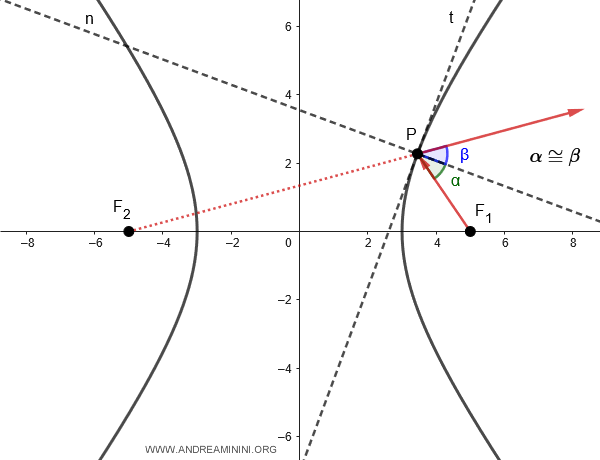
And so on.
