Equation of a Hyperbola Given Its Eccentricity and a Focus

To find the equation of a hyperbola centered at the origin, given its eccentricity and the coordinates of a focus, follow these steps:

• If the focus lies on the x-axis, the equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ with the eccentricity defined as $ e = \frac{c}{a} $.
• If the focus lies on the y-axis, the equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$  with the eccentricity defined as $ e = \frac{c}{b} $.

The relationship between the semi-major and semi-minor axes, and the distance of the foci from the center, is given by the formula $$ c^2 = a^2 + b^2 $$

By solving this system of equations, you can determine the lengths of the semi-axes $ a $ and $ b $, which are necessary to write the equation of the hyperbola.

A Practical Example

Let's consider a hyperbola centered at the origin, with a focus at $ F(3, 0) $ and an eccentricity $ e = \frac{3}{2} $.

Since the foci are on the x-axis, the equation of the hyperbola takes the form:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

The eccentricity of a hyperbola with foci on the x-axis is given by:

$$ e = \frac{c}{a} $$

We can set up a system of equations based on this information:

$$ \begin{cases} e = \frac{c}{a} \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \end{cases} $$

Given that the eccentricity is $ e = \frac{3}{2} $ and the focus is at $ F(c, 0) = (3, 0) $, where $ c=3 $, we have:

$$ \begin{cases} \frac{3}{2} = \frac{3}{a} \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \end{cases} $$

This simplifies to:

$$ \begin{cases} a = 3 \times \frac{2}{3} \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \end{cases} $$

$$ \begin{cases} a = 2 \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \end{cases} $$

Thus, the vertex of the hyperbola on the x-axis is located at $ A(a, 0) = (2, 0) $.

Once we know $ a = 2 $, we can find the semi-minor axis $ b $ using the relationship $ c^2 = a^2 + b^2 $.

$$ c^2 = a^2 + b^2 $$

Where $ c=3 $ and $ a = 2 $:

$$ 3^2 = 2^2 + b^2 $$

$$ 9 = 4 + b^2 $$

$$ b^2 = 9 - 4 $$

$$ b^2 = 5 $$

$$ b = \sqrt{5} $$

At this point, we can substitute $ a=2 $ and $ b=\sqrt{5} $ into the standard equation of the hyperbola:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{4} - \frac{y^2}{5} = 1 $$

This is the equation of the hyperbola centered at the origin with a focus at $ F(3, 0) $ and an eccentricity $ e = \frac{3}{2} $.

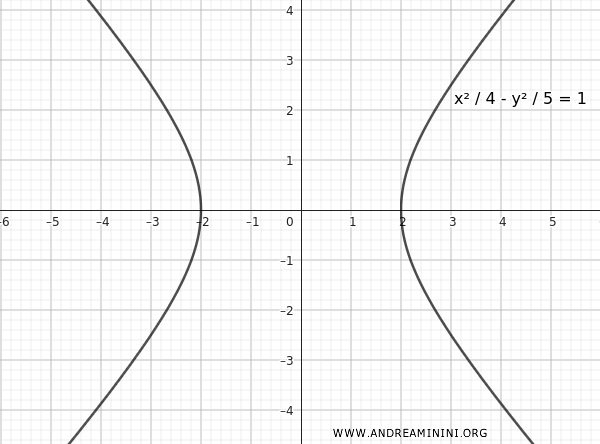
And that's how it's done.