Equation of a Hyperbola Given the Eccentricity and a Vertex
To derive the equation of a hyperbola centered at the origin, given the eccentricity and one vertex $ A(a;0) $ or $ B(0;b) $, follow these steps:
- If the foci lie on the x-axis, the equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ and the eccentricity is given by $$ e = \frac{c}{a} $$
- If the foci lie on the y-axis, the equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ and the eccentricity is $$ e = \frac{c}{b} $$
In both cases, the relationship between the semi-axes $ a $, $ b $, and the distance from the center to a focus $ c $ is:
$$ c^2 = a^2 + b^2 $$
Note: If it's not clear from the problem which axis contains the foci, you should consider both scenarios: the transverse axis being either the x-axis or the y-axis.
A Practical Example
Let's consider a hyperbola centered at the origin with a non-real vertex at $ A(-2;0) $ and an eccentricity of $ e = \frac{3 \sqrt{5}}{5} $.
Since the vertex $ A(-2;0) $ is on the x-axis, and the problem specifies that it is "non-real," the real axis (which contains the foci) must be the y-axis.
When the real (transverse) axis is the y-axis, the equation of the hyperbola is:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
The eccentricity of the hyperbola is defined as:
$$ e = \frac{c}{b} $$
We can now set up the system of equations:
$$ \begin{cases} e = \frac{c}{b} \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 \end{cases} $$
Given the eccentricity $ e = \frac{3 \sqrt{5}}{5} $ and the vertex coordinates $ A(a;0) = (2;0) $, where $ a = 2 $, we have:
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{c}{b} \\ \\ \frac{x^2}{2^2} - \frac{y^2}{b^2} = 1 \end{cases} $$
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{c}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
Knowing that $ c^2 = a^2 + b^2 $, we can express $ c $ as $ c = \sqrt{a^2 + b^2} $ with $ a = 2 $:
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{\sqrt{a^2 + b^2}}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{\sqrt{2^2 + b^2}}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{\sqrt{4 + b^2}}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
Next, we square both sides of the first equation:
$$ \begin{cases} \left( \frac{3 \sqrt{5}}{5} \right)^2 = \left( \frac{\sqrt{4 + b^2}}{b} \right)^2 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9 \cdot 5}{25} = \frac{4 + b^2}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9}{5} = \frac{4}{b^2} + \frac{b^2}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9}{5} = \frac{4}{b^2} + 1 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9}{5} - 1 = \frac{4}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9 - 5}{5} = \frac{4}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{4}{5} = \frac{4}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} b^2 = \frac{5}{4} \times 4 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} b^2 = 5 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \sqrt{b^2} = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} b = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
Now that we know $ b = \sqrt{5} $, we can substitute it back into the second equation:
$$ \begin{cases} b = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{(\sqrt{5})^2} = -1 \end{cases} $$
$$ \begin{cases} b = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{5} = -1 \end{cases} $$
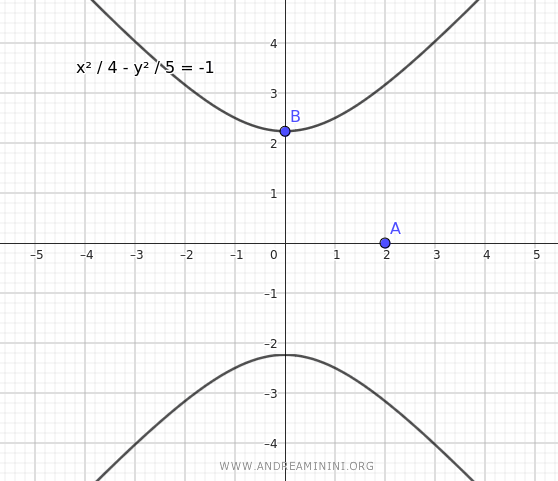
Therefore, the equation of the hyperbola centered at the origin with a non-real vertex at $ A(-2;0) $ and an eccentricity of $ e = \frac{3 \sqrt{5}}{5} $ is:
$$ \frac{x^2}{4} - \frac{y^2}{5} = -1 $$
Here is the graphical representation:
And so on.
