Equation of a Hyperbola Given a Vertex and a Focus
To find the equation of a hyperbola centered at the origin, given the coordinates of a focus and a vertex, follow these steps:
- If the focus \((c, 0)\) and the vertex \((a, 0)\) are on the \(x\)-axis, then the equation is:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ If instead the focus \((0, c)\) and the vertex \((0, b)\) are on the \(y\)-axis, the equation is:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ - Calculate \(b\) using the relationship between \(a\), \(b\), and \(c\): $$ c^2 = a^2 + b^2 $$
Once you know the lengths \(a\) and \(b\) for the transverse and non-transverse axes, you can write the equation of the hyperbola.
Example
Consider a hyperbola centered at the origin \( O(0,0) \), with a focus at \(F(5, 0)\) and a vertex at \(A(3, 0)\).
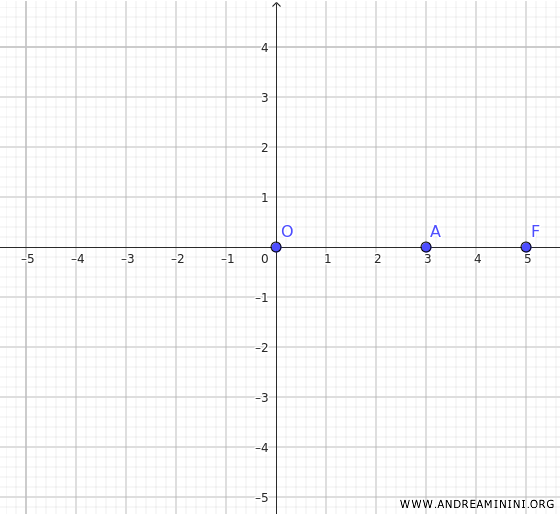
The foci are on the \(x\)-axis, so the equation of the hyperbola is:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Since the hyperbola is symmetric with respect to the center and the axes, knowing the coordinates of one focus \(F(5, 0)\) allows us to determine the other focus \(F_2(-5,0) \).
In both cases, the distance from the focus to the center is \( c = 5 \).
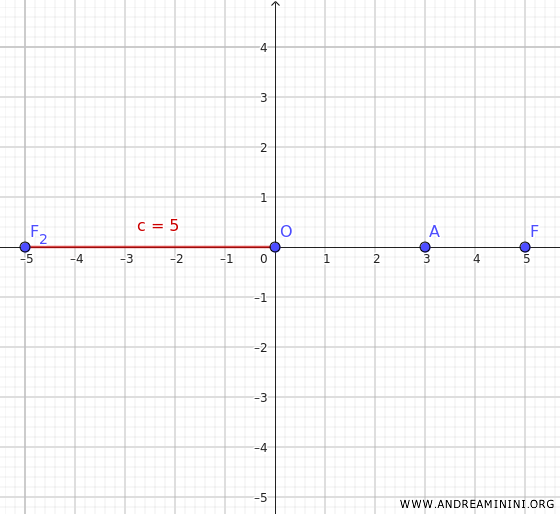
Similarly, knowing the coordinates of one vertex \(A(3, 0)\), we can find the other vertex \(A_2(-3, 0)\).
Thus, the distance of each vertex from the center is \( a = 3 \).
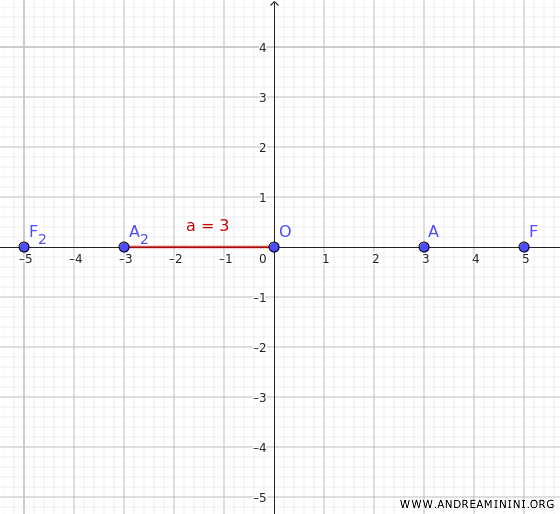
Next, use the following relationship to find the length of the non-transverse axis \( b \):
$$ c^2 = a^2 + b^2 $$
$$ 5^2 = 3^2 + b^2 $$
$$ 25 = 9 + b^2 $$
$$ b^2 = 25 - 9 $$
$$ b^2 = 16 $$
$$ \sqrt{b^2} = \sqrt{16} $$
$$ b = \pm 4 $$
Since \( b \) represents a length, we discard the negative value.
$$ b = 4 $$
Now that we know \( a=3 \) and \( b = 4 \), we can write the equation of the hyperbola:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Substituting the values of \(a\) and \(b\):
$$ \frac{x^2}{3^2} - \frac{y^2}{4^2} = 1 $$
$$ \frac{x^2}{9} - \frac{y^2}{16} = 1 $$
Therefore, the equation of the hyperbola centered at the origin with a focus at \((5, 0)\) and a vertex at \((3, 0)\) is \( \frac{x^2}{9} - \frac{y^2}{16} = 1 \).
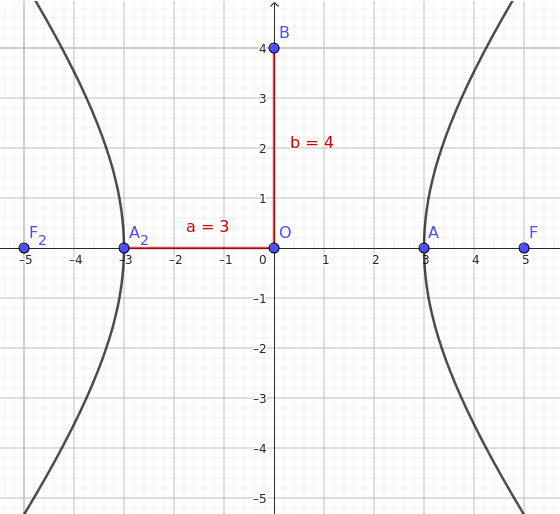
And so forth.
