Equation of a Hyperbola Passing Through Two Points
To find the equation of a hyperbola centered at the origin that passes through two given points $ P_1(x_1;y_1) $ and $ P_2(x_2;y_2) $, follow these steps:
First, determine the transverse axis, the axis along which the foci lie:
- If the transverse axis is the x-axis, the standard equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
- If the transverse axis is the y-axis, the standard equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
If it’s unclear which axis is the transverse one, you should consider both possibilities.
Next, substitute the coordinates of the known points $ P_1(x_1;y_1) $ and $ P_2(x_2;y_2) $ into the standard equation, creating a system of equations to solve for $ a^2 $ and $ b^2 $.
A Practical Example
Let’s consider a hyperbola with foci along the y-axis that passes through the points $ P_1(1; \frac{\sqrt{5}}{2}) $ and $ P_2(4;\sqrt{5}) $.
Since the foci are on the y-axis, the standard equation of the hyperbola is:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
We then create a system of equations by substituting the coordinates of the given points $ P_1(1; \frac{\sqrt{5}}{2}) $ and $ P_2(4;\sqrt{5}) $:
$$ \begin{cases} \frac{x_1^2}{a^2} - \frac{y_1^2}{b^2} = -1 \\ \\ \frac{x_2^2}{a^2} - \frac{y_2^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{1^2}{a^2} - \frac{(\frac{\sqrt{5}}{2})^2}{b^2} = -1 \\ \\ \frac{4^2}{a^2} - \frac{(\sqrt{5})^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{1}{a^2} - \frac{\frac{5}{4}}{b^2} = -1 \\ \\ \frac{16}{a^2} - \frac{5}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{1}{a^2} - \frac{5}{4} \cdot \frac{1}{b^2} = -1 \\ \\ \frac{16b^2-5a^2}{a^2b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{1}{a^2} - \frac{5}{4b^2} = -1 \\ \\ \frac{16b^2-5a^2}{a^2b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{4b^2-5a^2}{4a^2b^2} = -1 \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
$$ \begin{cases} 4b^2-5a^2 = -4a^2b^2 \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
Now, solve the system by isolating $ b^2 $ in the first equation and substituting it into the second equation.
$$ \begin{cases} 4b^2 + 4a^2b^2 = 5a^2 \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
$$ \begin{cases} b^2 \cdot (4 + 4a^2) = 5a^2 \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
$$ \begin{cases} b^2 = \frac{5a^2}{4 + 4a^2} \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 16b^2-5a^2 = -a^2b^2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 16 \cdot \left(\sqrt{ \frac{5a^2}{4 + 4a^2} }\right)^2 - 5a^2 = -a^2 \cdot \left(\sqrt{ \frac{5a^2}{4 + 4a^2} }\right)^2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 16 \cdot \frac{5a^2}{4 + 4a^2} -5a^2 = -a^2 \cdot \frac{5a^2}{4 + 4a^2} \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ \frac{80a^2 - 5a^2 \cdot (4 + 4a^2)}{4 + 4a^2} = -\frac{5a^4}{4 + 4a^2} \end{cases} $$
Multiply both sides of the second equation by $ 4+4a^2 $ and simplify:
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 80a^2 - 5a^2 \cdot (4 + 4a^2) = -5a^4 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 80a^2 - 20a^2 - 20a^4 + 5a^4 = 0 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ -15a^4 + 60a^2 = 0 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ a^2(60-15a^2) = 0 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5a^2}{4 + 4a^2} } \\ \\ 3a^2(20-5a^2) = 0 \end{cases} $$
The second equation has two roots: $ a=0 $ and $ a = \sqrt{\frac{20}{5}} = \sqrt{4} = 2 $.
Since a length cannot be zero, we discard the zero value and consider only the positive root $ a=2 $.
With the length of the semi-transverse axis now known as $ a=2 $, we substitute this into the first equation to find the corresponding value of $ b $:
$$ \begin{cases} b = \sqrt{ \frac{5 \cdot 2^2}{4 + 4 \cdot 2^2} } \\ \\ a = 2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{5 \cdot 4}{4 + 4 \cdot 4} } \\ \\ a = 2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{20}{4 + 16} } \\ \\ a = 2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ \frac{20}{20} } \\ \\ a = 2 \end{cases} $$
$$ \begin{cases} b = \sqrt{ 1 } \\ \\ a = 2 \end{cases} $$
$$ \begin{cases} b = 1 \\ \\ a = 2 \end{cases} $$
Therefore, the semi-axes of the hyperbola are $ a =2 $ and $ b = 1 $.
Substituting these values into the standard equation of the hyperbola gives:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
$$ \frac{x^2}{2^2} - \frac{y^2}{1^2} = -1 $$
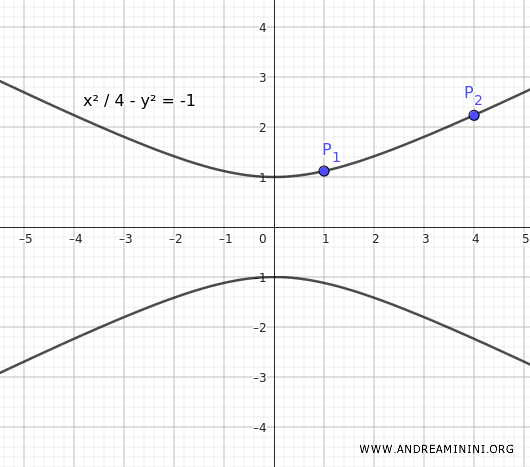
$$ \frac{x^2}{4} - y^2 = -1 $$
This is the equation of the hyperbola with foci on the y-axis that passes through the points $ P_1(1; \frac{\sqrt{5}}{2}) $ and $ P_2(4;\sqrt{5}) $.
And so on.
