Equation of a Hyperbola Given a Point and a Vertex
When I know the coordinates of a point $ P(x_0;y_0) $ and a vertex A or B of a hyperbola centered at the origin, I can complete the equation by following these steps:
Since I do not know the coordinates of the foci, I cannot determine if the major axis of the hyperbola is horizontal or vertical, so I must consider both possibilities:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = \pm 1 $$
I substitute the coordinates of the known point and the vertex into the equation.
Then, I solve the equation to determine the other vertex.
Example
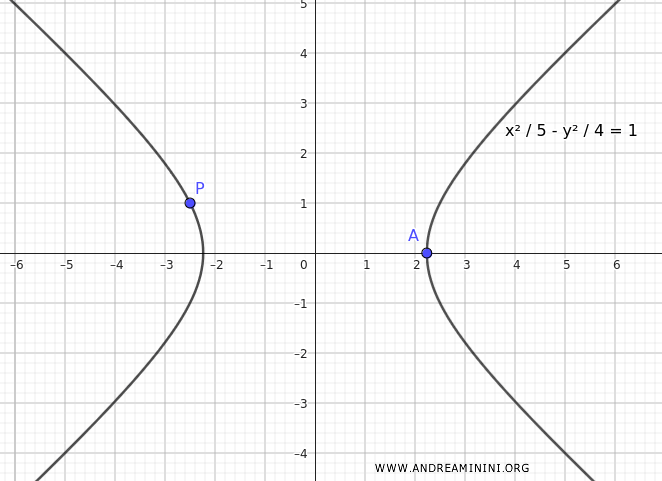
In this exercise, I need to find the equation of a hyperbola centered at the origin of the Cartesian axes with a real vertex at $ A( \sqrt{5};0 ) $ and passing through the point $ P(- \frac{5}{2};1) $
The real vertex is located on the x-axis, so the major axis where the foci of the hyperbola are found is horizontal.
Therefore, the equation of the hyperbola is as follows:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Let's rewrite it in a form that's more convenient for the calculations that follow:
$$ \frac{b^2x^2-a^2y^2}{a^2b^2} = 1 $$
$$ b^2x^2-a^2y^2 = a^2b^2 $$
I substitute the coordinates of the known point $ P(- \frac{5}{2};1) $ into the equation of the hyperbola, which means $ x= - \frac{5}{2} $ and $ y=1 $.
$$ b^2 \cdot (- \frac{5}{2})^2-a^2 \cdot(1)^2 = a^2b^2 $$
$$ \frac{25}{4} b^2 -a^2 = a^2b^2 $$
$$ \frac{25}{4}b^2 -a^2 = a^2b^2 $$
Now, I substitute the coordinates of the known vertex $ A(a;0)=( \sqrt{5};0 ) $, which means $ a=\sqrt{5} $
$$ \frac{25}{4}b^2 -( \sqrt{5} )^2 = ( \sqrt{5} )^2b^2 $$
$$ \frac{25}{4}b^2 - 5 = 5b^2 $$
$$ \frac{25}{4}b^2 - 5b^2 = 5 $$
$$ \frac{25b^2-20b^2}{4} = 5 $$
$$ \frac{5b^2}{4} = 5 $$
$$ b^2 = 5 \cdot \frac{4}{5} $$
$$ b^2 = 4 $$
Therefore, if $ b^2 = 4 $ the minor axis is $ b=2 $
At this point, I substitute $ a= \sqrt{5} $ and $ b=2 $ into the standard equation of the hyperbola.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{(\sqrt{5})^2} - \frac{y^2}{2^2} = 1 $$
$$ \frac{x^2}{5} - \frac{y^2}{4} = 1 $$
This is the equation of the hyperbola centered at the origin with a real vertex at $ A( \sqrt{5};0 ) $ and passing through the point $ P(- \frac{5}{2};1) $
And so on.
