Finding the Equation of a Hyperbola Given an Asymptote and a Focus

To find the equation of a hyperbola centered at the origin, knowing the location of a focus helps determine whether the transverse axis lies along the x-axis or the y-axis.

• If the focus is at $ F(c;0) $, the transverse axis is the x-axis, and the equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
• If the focus is at $ F(0;c) $, the transverse axis is the y-axis, and the equation of the hyperbola becomes $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$

In either case, the equations for the asymptotes of the hyperbola are:

$$ y = \pm \frac{b}{a} x $$

The relationship between the semi-axes $ a $ and $ b $ and the distance $ c $ from the center to the focus is always:

$$ c^2 = a^2 + b^2 $$

With these elements, you can determine the equation of the hyperbola.

A Practical Example

Let’s consider a hyperbola with a focus at

$$ F(c;0) = F(5;0) $$

and an asymptote given by

$$ y = \sqrt{\frac{2}{3}} x $$

Since the focus is on the x-axis, the equation of the hyperbola is:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

To find the semi-axes $ a $ and $ b $, we use a system of equations involving the asymptote equation and the relationship between the semi-axes.

$$ \begin{cases} y = \pm \frac{b}{a} x \\ \\ c^2 = a^2 + b^2 \end{cases} $$

We know the equation of the asymptote $ y = \sqrt{\frac{2}{3}} x $ and the distance from the center to the focus, $ c = 5 $.

$$ \begin{cases} \sqrt{\frac{2}{3}} x = \frac{b}{a} x \\ \\ 5^2 = a^2 + b^2 \end{cases} $$

Dividing both sides of the first equation by $ x $, we get:

$$ \begin{cases} \sqrt{\frac{2}{3}} = \frac{b}{a} \\ \\ 25 = a^2 + b^2 \end{cases} $$

We can now solve for $ b $ in the first equation:

$$ \begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ 25 = a^2 + b^2 \end{cases} $$

Substituting $ b $ into the second equation gives:

$$ \begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ 25 = a^2 + \left(\sqrt{\frac{2}{3}} a\right)^2 \end{cases} $$

$$ \begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ 25 = a^2 + \frac{2}{3} a^2 \end{cases} $$

$$ \begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ 25 = \frac{5a^2}{3} \end{cases} $$

$$ \begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ a^2 = 25 \cdot \frac{3}{5} \end{cases} $$

$$ \begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ a^2 = 15 \end{cases} $$

$$ \begin{cases} b = \sqrt{\frac{2}{3}} a \\ \\ a = \sqrt{15} \end{cases} $$

Once we have $ a = \sqrt{15} $, we can substitute it back into the first equation to find $ b $:

$$ \begin{cases} b = \sqrt{\frac{2}{3}} \sqrt{15} \\ \\ a = \sqrt{15} \end{cases} $$

$$ \begin{cases} b = \sqrt{\frac{2}{3} \cdot 15} \\ \\ a = \sqrt{15} \end{cases} $$

$$ \begin{cases} b = \sqrt{10} \\ \\ a = \sqrt{15} \end{cases} $$

So, the lengths of the semi-axes are $ a = \sqrt{15} $ and $ b = \sqrt{10} $, which can be substituted into the standard equation of the hyperbola.

$$ \frac{x^2}{(\sqrt{15})^2} - \frac{y^2}{(\sqrt{10})^2} = 1 $$

$$ \frac{x^2}{15} - \frac{y^2}{10} = 1 $$

This is the equation of the hyperbola with a focus at $ F(c;0) = F(5;0) $ and an asymptote $ y = \sqrt{\frac{2}{3}} x $.

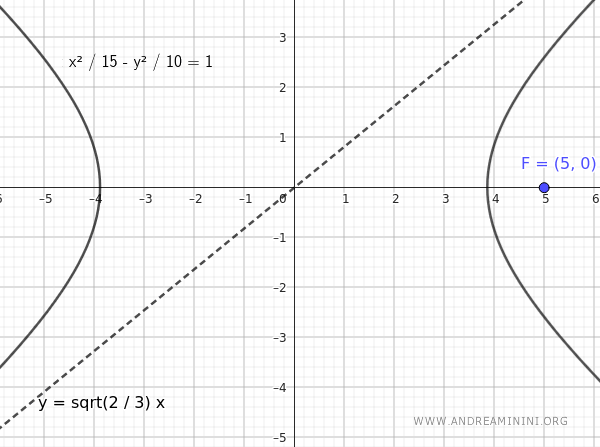
And that's how you derive the equation.